Ermitteln Sie grafisch diejenige Stelle \(x_0 \in \mathbb R^+\), für die gilt: Die lokale Änderungsrate von \(g\) an der Stelle \(x_0\) stimmt mit der mittleren Änderungsrate von \(g\) im Intervall \([1;4]\) überein.
(3 BE)
Lösung zu Teilaufgabe 2b
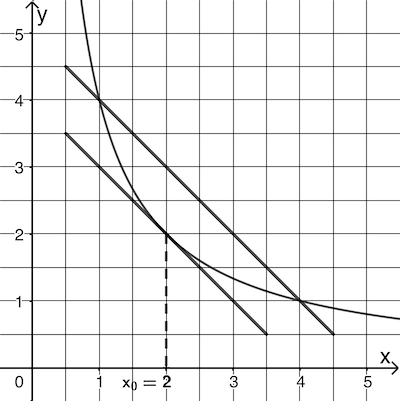 Abb. 1
Abb. 1
Ausführliche Erklärung (nicht verlangt)
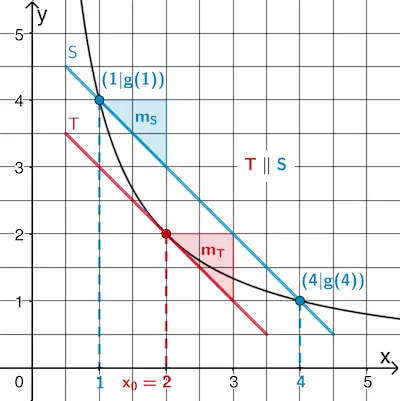
Die Steigung \(\textcolor{#0087c1}{m_S}\) der Sekante \(\textcolor{#0087c1}{S}\) durch die Punkte \(\textcolor{#0087c1}{(1|g(1))}\) und \(\textcolor{#0087c1}{(4|g(4))}\) beschreibt die mittlere Änderungsrate von \(g\) im Intervall \(\textcolor{#0087c1}{[1;4]}\).
Differenzenquotient oder mittlere Änderungsrate
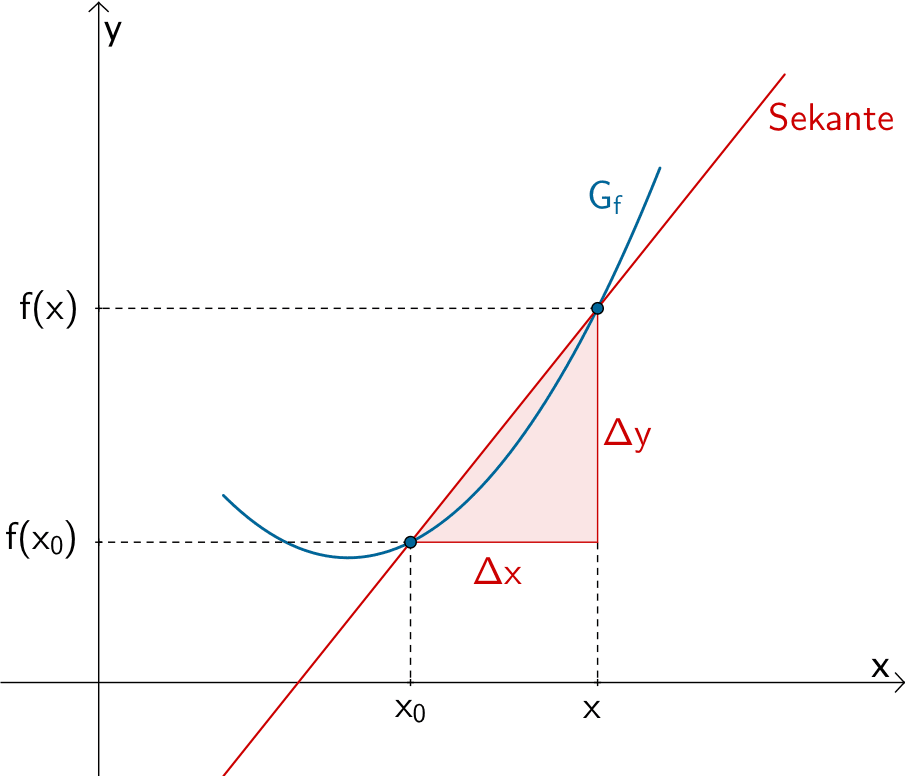
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
Die Steigung \(\textcolor{#cc071e}{m_T}\) der zur Sekante \(\textcolor{#0087c1}{S}\) parallelen Tangente \(\textcolor{#cc071e}{T}\) an den Graphen von \(g\) beschreibt die lokale Änderungsrate von \(g\) an der Stelle \(\textcolor{#cc071e}{x_0}\) des Berührpunkts der Tangente. Sie stimmt mit der mittleren Änderungsrate von \(g\) im Intervall \(\textcolor{#0087c1}{[1;4]}\) überein.
Differentialquotient oder lokale bzw. momentane Änderungsrate
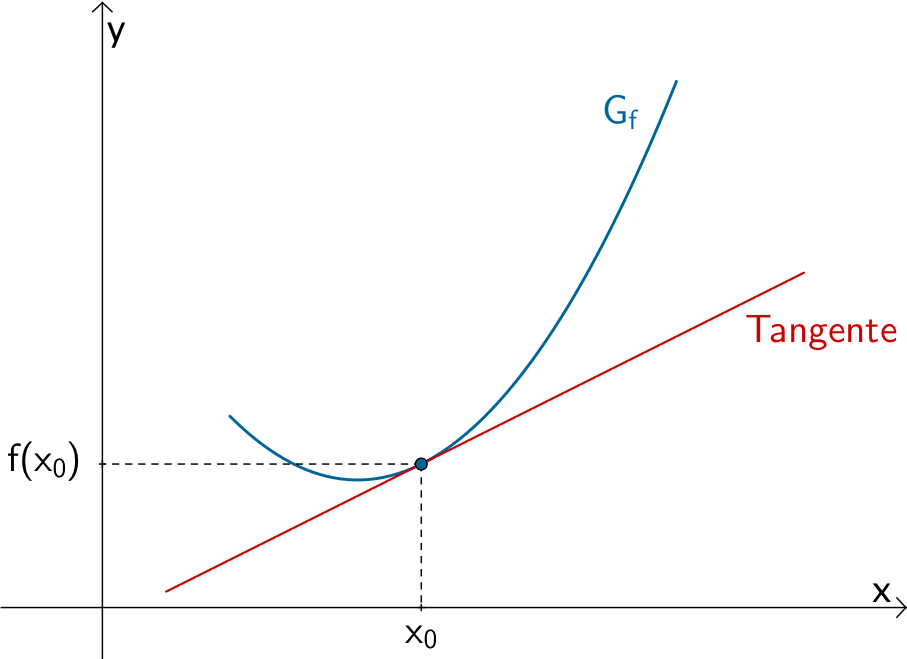
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Es ergibt sich: \(\textcolor{#cc071e}{x_0 = 2}\).
Ergänzung: Rechnerische Bestimmung von \(x_0\) (nicht verlangt)
Gelegentlich wird von diesem Aufgabentyp auch die rechnerische Lösung verlangt. (vgl. Mathematik Abitur Bayern 2019 Prüfungsteil B Analysis 1 Teilaufgabe 2b) Deshalb sei diese ergänzend aufgeführt.
Mittlere Änderungsrate von \(g\) im Intervall \(\textcolor{#0087c1}{[1;4]}\):
Differenzenquotient oder mittlere Änderungsrate

Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[\textcolor{#0087c1}{m_S} = \frac{\textcolor{#0087c1}{g(4)} - \textcolor{#0087c1}{g(1)}}{\textcolor{#0087c1}{4} - \textcolor{#0087c1}{1}}\]
Lokale Änderungsrate von \(g\) an der Stelle \(\textcolor{#cc071e}{x_0}\) des Berührpunkts der Tangente an den Graphen von \(g\):
Differentialquotient oder lokale bzw. momentane Änderungsrate

Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\(\textcolor{#cc071e}{m_T} = \textcolor{#cc071e}{g'(x_0)}\)
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[g(x) = \frac{4}{x} = 4 \cdot x^{-1}; \;D_g = \mathbb R^+\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[g'(x) = 4 \cdot (-1) \cdot x^{-2} = -\frac{4}{x^2}\]
Bedingung:
Die lokale Änderungsrate von \(g\) an der Stelle \(\textcolor{#cc071e}{x_0}\) stimmt mit der mittleren Änderungsrate von \(g\) im Intervall \(\textcolor{#0087c1}{[1;4]}\) überein.
\[\begin{align*} \textcolor{#0087c1}{m_S} &= \textcolor{#cc071e}{m_T} \\[0.8em] \frac{\textcolor{#0087c1}{g(4)} - \textcolor{#0087c1}{g(1)}}{\textcolor{#0087c1}{4} - \textcolor{#0087c1}{1}} &= \textcolor{#cc071e}{g'(x_0)} &&| \; g(x) = \frac{4}{x}; \;g'(x) = -\frac{4}{x^{2}} \\[0.8em] \frac{\textcolor{#0087c1}{\frac{4}{4}} - \textcolor{#0087c1}{\frac{4}{1}}}{\textcolor{#0087c1}{4} - \textcolor{#0087c1}{1}} &= \textcolor{#cc071e}{-\frac{4}{x_0^2}} \\[0.8em] \textcolor{#0087c1}{-1} &= \textcolor{#cc071e}{-\frac{4}{x_0^2}} &&| \cdot (-x_0^2) \\[0.8em] x_{0}^{2} &= 4 &&| \; \sqrt{\dots}\,, \; D_g = \mathbb R^+ \\[0.8em] x_0 &= 2 \end{align*}\]


