Die Funktion \(g\) ist an der Stelle \(x = 5\) nicht differenzierbar.

(2 BE)

Lösung zu Teilaufgabe 2b

1. Betragsfunktionen, deren Argument an der Stelle \(x = 5\) das Vorzeichen wechselt

Als Argument der Betragsfunktion kommt jeder in \(\mathbb R\) definierte Funktionsterm infrage, der an der Stelle \(x = 5\) eine Nullstelle ungerader Ordnung besitzt.

Beispiel:

\[\begin{align*} g_1(x) &= \vert x - 5 \vert & &D_{g_1} = \mathbb R \\[0.8em] &= \begin{cases} -(x - 5)\,, &\text{falls} \enspace x < 5 \\[0.8em] \hspace{18px} x - 5\,, &\text{falls} \enspace x \geq 5 \end{cases} \end{align*}\]

Grenzwertbetrachtung für \(x \to 5\,\):

\[\lim \limits_{x\,\to\, 5^-} \frac{g_1(x) - g_1(5)}{x - 5} = \lim \limits_{x\,\to\,5^-} \frac{-(x - 5) - 0}{x - 5} = \lim \limits_{x\,\to\,5^-} -1 = -1\]

\[\lim \limits_{x\,\to\, 5^+} \frac{g_1(x) - g_1(5)}{x - 5} = \lim \limits_{x\,\to\,5^+} \frac{x - 5 - 0}{x - 5} = \lim \limits_{x\,\to\,5^+} 1 = 1\]

Da der linksseitige und der rechtsseitige Grenzwert verschieden sind, existiert der Grenzwert \(\displaystyle \lim \limits_{x\,\to\,5} \frac{g_1(x) - g(5)}{x - 5}\,\) nicht. Somit ist die Betragsfunktion \(g_1(x) = \vert x - 5 \vert\) an der Stelle \(x = 5\) nicht differenzierbar.

weitere Beispiele:

\[\begin{align*} g_2(x) &= \vert (x - 1)(x - 5) \vert & &D_{g_2} = \mathbb R \\[0.8em] &= \vert x^2 -6x + 5 \vert \\[0.8em] &= \begin{cases} -(x^2 - 6x + 5)\,, &\text{falls} \enspace x \in \; ]1;5[ \\[0.8em] \hspace{18px} x^2 - 6x + 5\,, &\text{falls} \enspace x \in \; ]-\infty;1] \cup [5;\infty[ \end{cases} \\[3em] g_3(x) &= \vert -e^{x - 5} + 1 \vert & &D_{g_3} = \mathbb R \\[0.8em] &= \begin{cases} \hspace{18px} -e^{x - 5} + 1\,, &\text{falls} \enspace x \leq 5 \\[0.8em] -\left( -e^{x - 5} + 1 \right)\,, &\text{falls} \enspace x > 5 \end{cases} \end{align*}\]

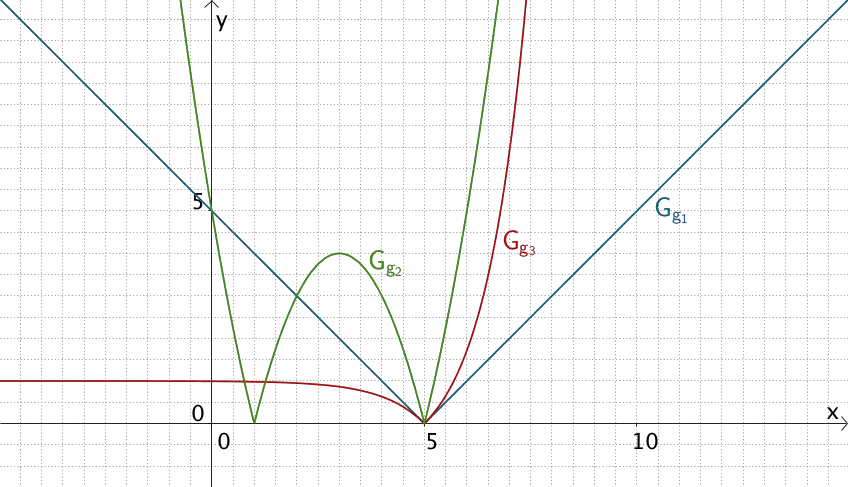
Graphen der Betragsfunktionen \(g_1\,\), \(g_2\,\) und \(g_3\), die an der Stelle \(x = 5\) nicht differezierbar sind.

2. Weitere abschnittsweise definierte Funktionen

Abschnittsweise definierte Funktionen \(g\), deren Teilfunktionen an der Stelle \(x = 5\) veschiedene Grenzwerte \(\displaystyle \lim \limits_{x\,\to\,5} \frac{g(x) - g(5)}{x - 5}\) aufweisen, sind an der Stelle \(x = 5\) nicht differenzierbar.

Beispiel:

\[g_4(x) = \begin{cases} \frac{1}{4}(x - 5)^2\,, &\text{falls} \enspace x \leq 5 \\[0.8em] \frac{1}{2}(x - 5)\,, &\text{falls} \enspace x > 5\end{cases} \qquad D_{g_4} = \mathbb R\]

Grenzwertbetrachtung für \(x \to 5\,\):

\[\lim \limits_{x\,\to\, 5^-} \frac{g_4(x) - g_4(5)}{x - 5} = \lim \limits_{x\,\to\,5^-} \frac{\frac{1}{4}(x - 5)^2 - 0}{x - 5} = \lim \limits_{x\,\to\,5^-} \frac{1}{4}(x - 5) = 0\]

\[\lim \limits_{x\,\to\, 5^+} \frac{g_4(x) - g_4(5)}{x - 5} = \lim \limits_{x\,\to\,5^+} \frac{\frac{1}{2}(x - 5) - 0}{x - 5} = \lim \limits_{x\,\to\,5^+} \frac{1}{2} = \frac{1}{2}\]

\[\Longrightarrow \quad \lim \limits_{x\,\to\, 5^-} \frac{g_4(x) - g_4(5)}{x - 5} \enspace \neq \enspace \lim \limits_{x\,\to\, 5^+} \frac{g_4(x) - g_4(5)}{x - 5}\]

\(\Longrightarrow \quad\) Die Funktion \(g_4\) ist an der Stelle \(x = 5\) nicht differenzierbar.

weitere Beispiele:

\[\begin{align*}g_5(x) &= \begin{cases} x\,, &\text{falls} \enspace x \leq 5 \\[0.8em] 5\,, &\text{falls} \enspace x > 5\end{cases} & &D_{g_5} = \mathbb R \\[3em] g_6(x) &= \begin{cases} 3\,, &\text{falls} \enspace x \leq 5 \\[0.8em] -2 \sqrt{x - 5} + 3\,, &\text{falls} \enspace x > 5\end{cases} & &D_{g_6} = \mathbb R\end{align*}\]

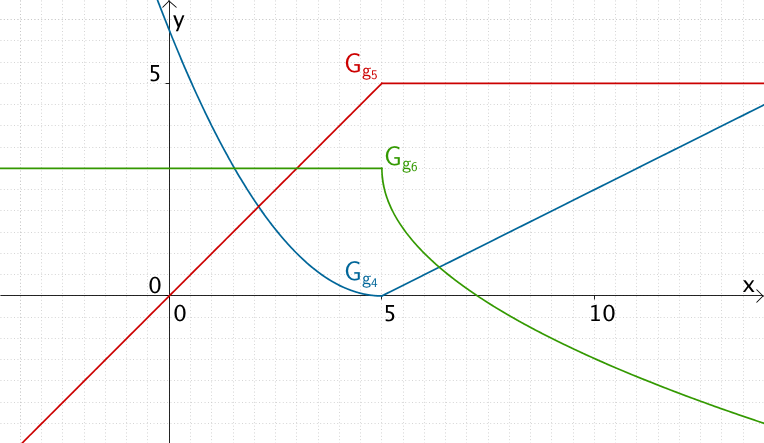
Graphen der abschnittsweise definierten Funktionen \(g_4\,\), \(g_5\) und \(g_6\,\), die an der Stelle \(x = 5\) nicht differenzierbar sind.

Ebenfalls denkbar ist eine abschnittsweise definierte Funktion, welche der Definitionslücke einer gebrochenrationalen Funktion einen separaten Funktionswert zuweist.

\[g_7(x) = \begin{cases} \frac{1}{x - 5}\,, &\text{falls} \enspace x \neq 5 \\[0.8em] 0\,, &\text{falls} \enspace x = 5  \end{cases} \qquad D_{g_7} = \mathbb R\]

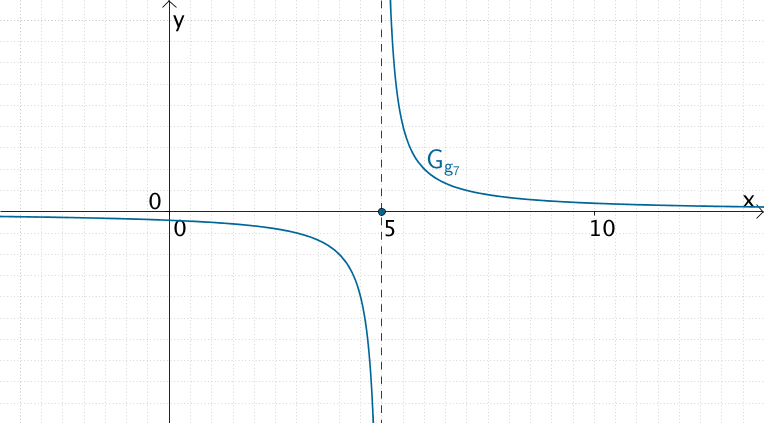
Die in \(\mathbb R\) abschnittsweise definierte Funktion \(g_7\) ist an der Stelle \(x = 5\) nicht differenzierbar.