Die Anzahl der Nullstellen von \(g_c\) hängt von \(c\) ab. Geben Sie jeweils einen möglichen Wert von \(c\) an, sodass gilt:
α) \(g_c\) hat keine Nullstelle.
β) \(g_c\) hat genau eine Nullstelle.
γ) \(g_c\) hat genau zwei Nullstellen.
(3 BE)
Lösung zu Teilaufgabe 2b
\[g_c(x) = f(x) + c\,; \quad c \in \mathbb R\]
Die \(y\)-Koordinate des (absoluten) Tiefpunkts \(TiP\,\left(-1|-\frac{2}{\sqrt{e}}\right)\) und die \(y\)-Koordinate des (absoluten) Hochpunkts \(HoP\,\left(1|\frac{2}{\sqrt{e}}\right)\) der Funktion \(f\) legen die Wertemenge \(\mathbb W_f\) fest.
\[\mathbb W_f = \left[ -\frac{2}{\sqrt{e}}; \frac{2}{\sqrt{e}} \right]\]
Mögliche Werte von \(c\), welche die Anzahl der Nullstellen von \(g_c\) bestimmen, orientieren sich an \(\mathbb W_f\).
α) \(g_c\) hat keine Nullstelle
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Für \(c \in \left]-\infty; -\frac{2}{\sqrt{e}}\right[ \cup \left]\frac{2}{\sqrt{e}}; + \infty\right[\) hat \(g_c\) keine Nullstelle.
\[\frac{2}{\sqrt{e}} \approx 1{,}21\]
Mögliche Werte von \(c\):
\(c = -2\) oder \(c = 2\)
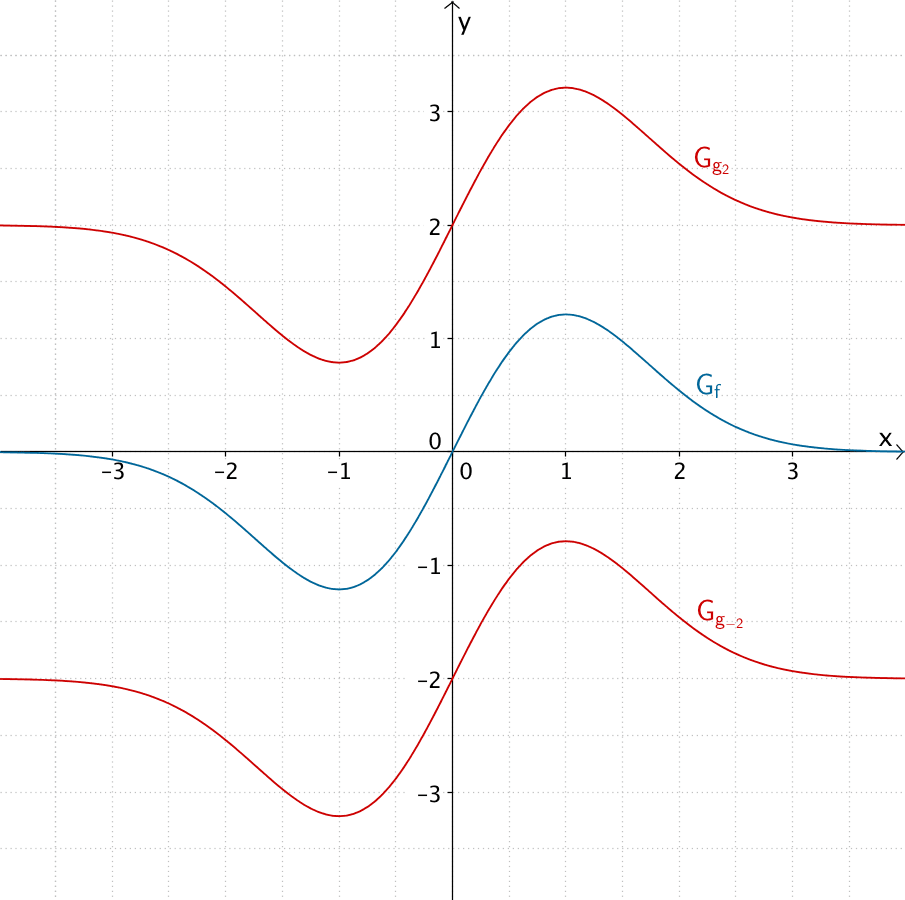
Die Graphen der Scharfunktionen \(g_{-2}\) und \(g_2\) haben keine Nullstelle.
β) \(g_c\) hat genau eine Nullstelle
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Für \(c = 0\) hat \(g_c\) genau die eine Nullstelle von \(f\), denn es gilt:
\[g_0(x) = f(x) + 0 = f(x)\]
Für \(c = -\frac{2}{\sqrt{e}}\) bzw. \(c = \frac{2}{\sqrt{e}}\) berührt der Hochpunkt \(HoP\,\left(1|\frac{2}{\sqrt{e}}\right)\) von \(G_f\) bzw. der Tiefpunkt \(TiP\,\left(1|-\frac{2}{\sqrt{e}}\right)\) von \(G_f\) die \(x\)-Achse. Somit hat \(g_c\) jeweils genau eine Nullstelle.
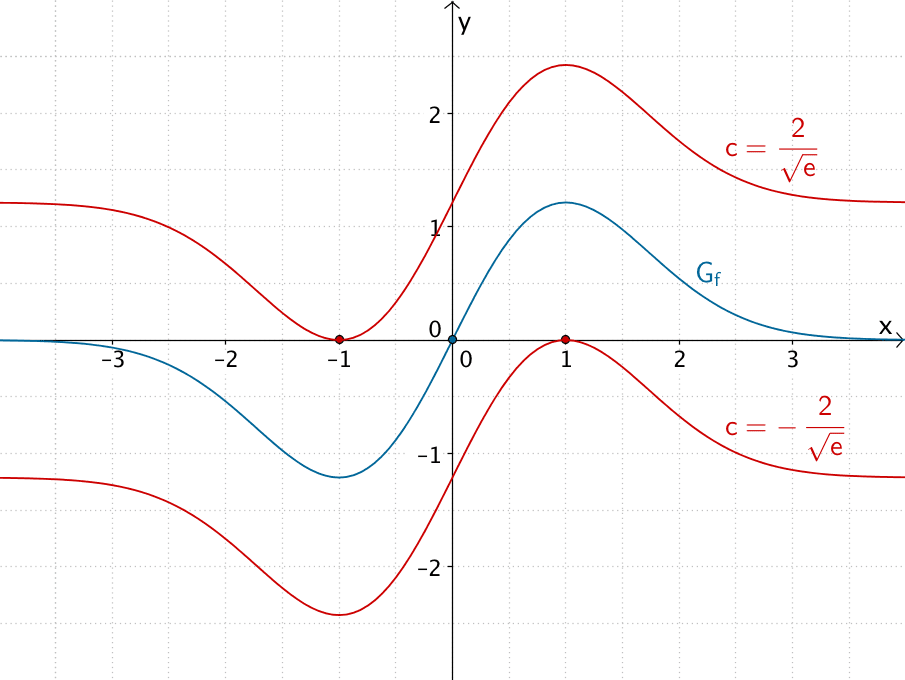
Graphen der Scharfunktionen von \(g_c\) mit genau einer Nullstelle.
γ) \(g_c\) hat genau zwei Nullstellen.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Für \(c \in \left]-\frac{2}{\sqrt{e}};0\right[ \cup \left]0;\frac{2}{\sqrt{e}}\right[\) hat \(g_c\) genau zwei Nullstellen.
\[\frac{2}{\sqrt{e}} \approx 1{,}21\]
Mögliche Werte von \(c\):
\(c = -1\) oder \(c = 1\)
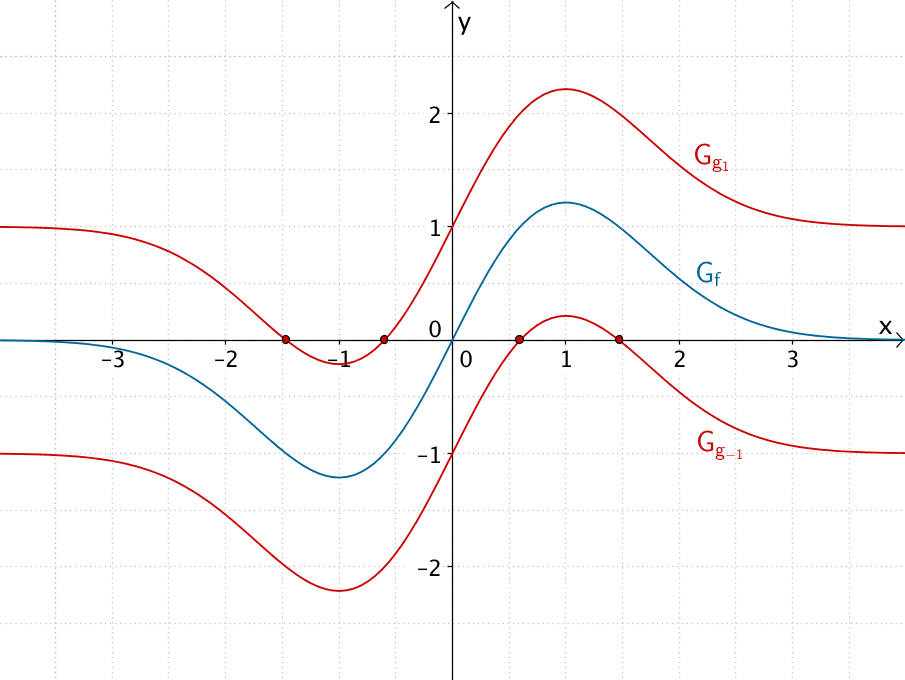
Die Graphen der Scharfunktionen \(g_{-1}\) und \(g_1\) haben haben genau zwei Nullstellen.

