- Details
- Kategorie: Analysis 2
Abbildung 1 zeigt den Graphen \(G_{f}\) einer ganzrationalen Funktion \(f\) drittens Grades mit Definitionsmenge \(\mathbb R\). \(G_{f}\) schneidet die \(x\)-Achse bei \(x = 0\), \(x = 5\) und \(x = 10\) und verläuft durch den Punkt \((1|2)\).
Ermitteln Sie einen Funktionsterm von \(f\).
(zur Kontrolle: \(f(x) = \frac{1}{18} \cdot (x^{3} - 15x^{2} + 50x)\))
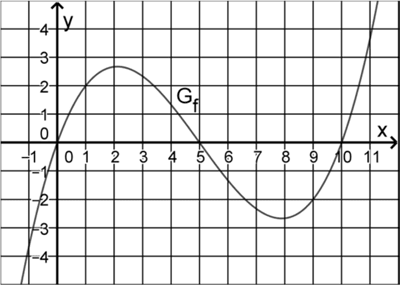Abb. 1
(4 BE)
- Details
- Kategorie: Analysis 2
Zeigen Sie, dass \(G_{f}\) im Punkt \(W(5|0)\) einen Wendepunkt besitzt, und ermitteln Sie eine Gleichung der Tangente an \(G_{f}\) im Punkt \(W\).
(6 BE)
- Details
- Kategorie: Analysis 2
\(G_{f}\) geht aus dem Graphen der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto \frac{1}{18} \cdot (x^{3} - 25x)\) durch Verschiebung in positive \(x\)-Richtung hervor. Ermitteln Sie, um wie viel der Graph von \(g\) dazu verschoben werden muss. Begründen Sie mithilfe der Funktion \(g\), dass der Graph von \(f\) symmetrisch bezüglich seines Wendepunkts ist.
(4 BE)
- Details
- Kategorie: Analysis 2
Im Folgenden wird die in \(\mathbb R\) definierte Funktion \(F_{1}\) mit \(\displaystyle F_{1}(x) = \int_{1}^{x} f(t) dt\) betrachtet.
\(F_{1}\) hat für \(0 \leq x \leq 10\) zwei ganzzahlige Nullstellen. Geben Sie diese an und begründen Sie Ihre Angabe.
(3 BE)
- Details
- Kategorie: Analysis 2
Begründen Sie mithilfe von Abbildung 1, dass \(F_{1}\) mindestens eine weitere positive Nullstelle hat.
(2 BE)
- Details
- Kategorie: Analysis 2
Für \(0 \leq x \leq 5\) gilt, dass der Graph von \(f\) und der Graph einer trigonometrischen Funktion \(h\)
● die gleichen Schnittpunkte mit der \(x\)-Achse besitzen,
● beide nicht unterhalb der \(x\)-Achse verlaufen,
● jeweils mit der \(x\)-Achse eine Fläche des Inhalts \(\frac{625}{72}\) einschließen.
Bestimmen Sie einen Term einer solchen Funktion \(h\).
(6 BE)
- Details
- Kategorie: Analysis 2
Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion \(K \colon x \mapsto x^{3} - 12x^{2} + 50x + 20\) mit \(x \in [0;9]\) beschrieben werden. Dabei gibt \(K(x)\) die Kosten in 1000 Euro an, die bei der Produktion von \(x\) Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von \(K\).
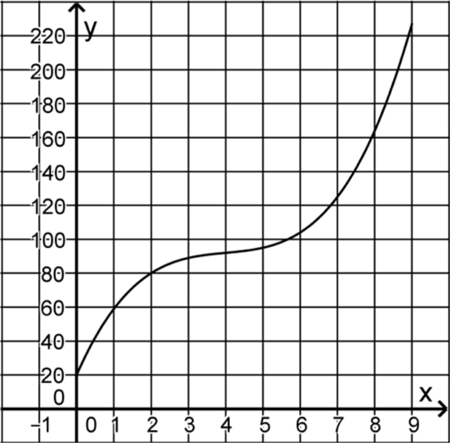Abb. 2
Geben Sie mithilfe von Abbildung 2
α) die Produktionsmenge an, bei der die Kosten 125 000 Euro betragen.
β) das Monotonieverhalten von \(K\) an und deuten Sie Ihre Angabe im Sachzusammenhang.
(3 BE)
- Details
- Kategorie: Analysis 2
Die Funktion \(E\) mit \(E(x) = 23x\) gibt für \(0 \leq x \leq 9\) den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von \(x\) Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion \(G\) gilt \(G(x) = E(x) - K(x)\). Positive Werte von \(G\) werden als Gewinn bezeichnet, negative als Verlust.
Zeigen Sie, dass das Unternehmen keinen Gewinn erzielt, wenn vier Kubikmeter der Flüssigkeit verkauft werden.
(2 BE)
- Details
- Kategorie: Analysis 2
Zeichnen Sie den Graphen von \(E\) in Abbildung 2 ein. Bestimmen Sie mithilfe der so entstehenden Darstellung den Bereich, in dem die verkaufte Menge der Flüssigkeit liegen muss, damit das Unternehmen einen Gewinn erzielt.
(3 BE)
- Details
- Kategorie: Analysis 2
Berechnen Sie, welche Menge der Flüssigkeit verkauft werden muss, damit das Unternehmen den größten Gewinn erzielt.
(5 BE)
