Drei kleine farbenfrohe Seesterne befinden sich am Meeresboden und werden im Modell durch die Punkte \(P\), \(Q\) und \(R\) dargestellt. Der Fotograf bewegt sich für seine Aufnahmen von der Stelle aus, die im Modell durch den Punkt \(K\) beschrieben wird, parallel zum Meeresboden und hat ein kegelförmiges Sichtfeld mit einem Öffnungswinkel von 90° (vgl. Abbildung).
Beurteilen Sie, ob der Fotograf auf diese Weise eine Stelle erreichen kann, an der er alle drei Seesterne gleichzeitig im Sichtfeld der Kamera sehen kann.
(3 BE)
Lösung zu Teilaufgabe g
Damit der Fotograf alle drei Seesterne gleichzeitig im Sichtfeld der Kamera sehen kann, muss der Durchmesser des Lichtkegels größer sein als der Durchmesser \([PQ]\) des Umkreises des Dreiecks \(PQR\).
Aus Teilaufgabe a ist bekannt: \(\overline{PQ} = 3\sqrt{2}\).
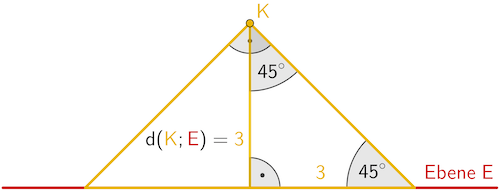
Planskizze (optional): Im Querschnitt bilden die Mantellinien des Lichtkegels mit der Ebene \(E\) ein gleichschenklig rechtwinkliges Dreieck. Die Höhe des Dreiecks entspricht dem Abstand \(d(\textcolor{#e9b509}{K};\textcolor{#cc071e}{E}) = \textcolor{#e9b509}{3}\). Die Höhe teilt das Dreieck wiederum in zwei gleichschenklig rechtwinklige Dreiecke mit den Schenkellängen \(\textcolor{#e9b509}{3}\). Der Kegel hat somit den Durchmesser \(2 \cdot \textcolor{#e9b509}{3} = 6\).
Mit \(6 > 3\sqrt{2}\) ist der Durchmesser des Lichtkegels größer als der Umkreis des Dreiecks \(\boldsymbol{PQR}\). Der Fotograf kann also eine Stelle erreichen, an der er alle drei Seesterne gleichzeitig im Sichtfeld der Kamera sehen kann.
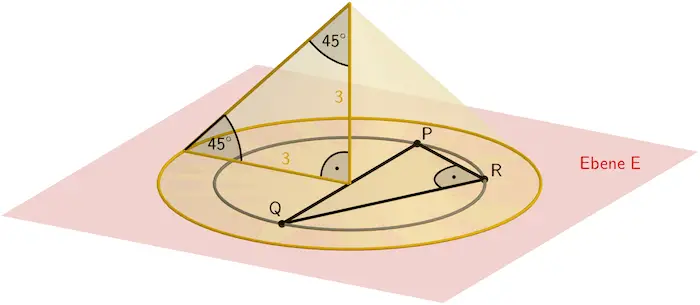 (Ergänzende Darstellung)
(Ergänzende Darstellung)


