In Urne A befinden sich zwei rote und drei weiße Kugeln. Urne B enthält drei rote und zwei weiße Kugeln. Betrachtet wird folgendes Zufallsexperiment:

Aus Urne A wird eine Kugel zufällig entnommen und in Urne B gelegt; danach wird aus Urne B eine Kugel zufällig entnommen und in Urne A gelegt.

Geben Sie alle Möglichkeiten für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments an.

(2 BE)

Lösung zu Teilaufgabe 1a

Wird im ersten Durchgang aus Urne A und im zweiten Durchgang aus Urne B eine Kugel derselben Farbe entnommen, ist der Inhalt in Urne A (und in Urne B) nach der Durchführung des Zufallsexperiments wieder derselbe wie zu Begin des Zufallsexperiments. Andernfalls ändert sich der Inhalt in Urne A (und in Urne B), d.h. es entstehen neue Anteile roter und weißer Kugel von insgesamt wieder fünf Kugeln nach der Durchführung des Zufallsexperiments. 

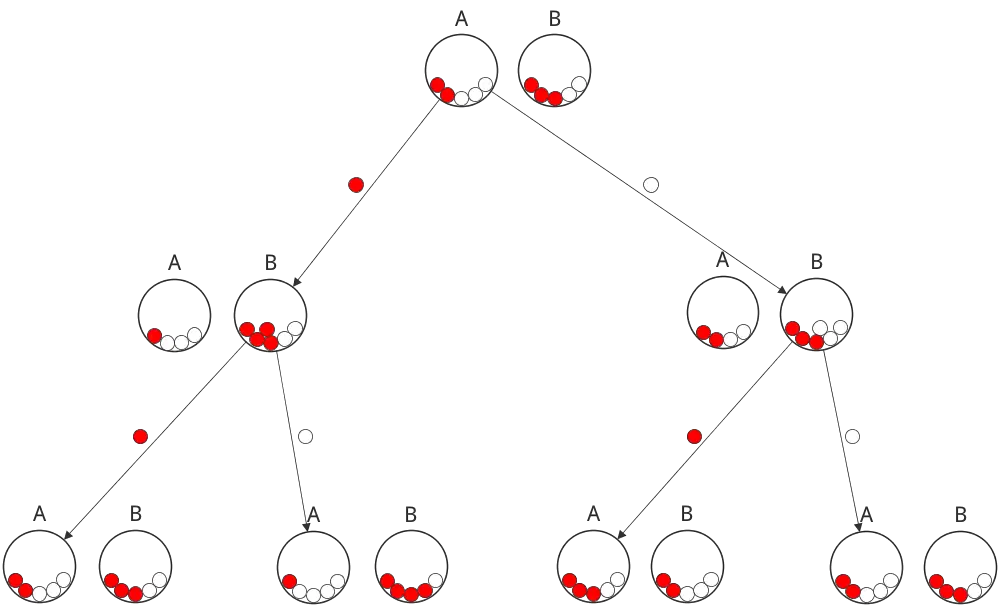
Baumdiagramm des Zufallsexperiments: Inhalt der Urne A und Inhalt der Urne B

Für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments ergeben sich die folgenden drei Möglichkeiten (mögliche Ergebnisse):

\[\Omega = \{(rrwww), (rwwww), (rrrww)\}\]

\(r\): rote Kugel, \(w\): weiße Kugel