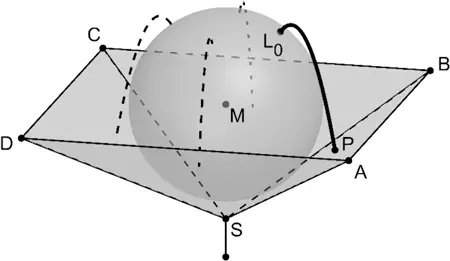
Ein auf einer Stange montierter Brunnen besteht aus einer Marmorkugel, die in einer Bronzeschale liegt. Die Marmorkugel berührt die vier Innenwände der Bronzeschale an jeweils genau einer Stelle. Die Bronzeschale wird im Modell durch die Seitenflächen der Pyramide \(ABCDS\) beschrieben, die Marmorkugel durch eine Kugel mit Mittelpunkt \(M(0|0|4)\) und Radius \(r\). Die \(x_{1}x_{2}\)-Ebene des Koordinatensystems stellt im Modell den horizontal verlaufenden Erdboden dar; eine Längeneinheit entspricht einem Dezimeter in der Realität.
Ermitteln Sie den Durchmesser der Marmorkugel auf Zentimeter genau.
(zur Kontrolle: \(r = \sqrt{6}\))
(4 BE)
Lösung zu Teilaufgabe d
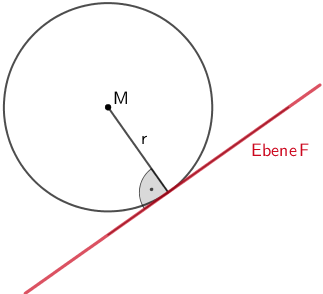
Planskizze (optional): Die Marmorkugel berühr die Seitenfläche \(ABS\) der Pyramide \(ABCDS\) und somit die Ebene \(F\) (vgl. Teilaufgabe b). Im Berührpunkt ist der Radius \(r\) der Kugel senkrecht zur Ebene \(F\). Folglich entspricht der Abstand des Mittelpunkts \(M\) von der Ebene \(F\) dem Radius der Kugel.
1. Möglichkeit: Abstand Punkt - Ebene, Hessesche Normalenform
\(F\colon x_{1} + x_{2} - 2x_{3} + 2 = 0; \; \textcolor{#0087c1}{\overrightarrow{n} = \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}}\) (vgl. Teilaufgabe b)
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Hessesche Normalenform (HNF) der Ebene \(F\) formulieren:
Hierfür wird die Gleichung der Ebene \(F\) in der Normalenform in Koordinatendarstellung (Koordinatenform) durch den Betrag des Normalenvektors \(\overrightarrow{n}\) dividiert.
\[\begin{align*}&F \colon \frac{x_{1} + x_{2} - 2x_{3} + 2}{\left| \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}} \right|} = 0 \quad \text{(HNF)} \\[0.8em] &F\colon \frac{x_{1} + x_{2} - 2x_{3} + 2}{\sqrt{1^{2} + 1^{2} + (-2)^{2}}} = 0 \quad \text{(HNF)} \\[0.8em] &F\colon \frac{x_{1} + x_{2} - 2x_{3} + 2}{\sqrt{6}} = 0 \quad \text{(HNF)}\end{align*}\]
(vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Hessesche Normalenform)
Daraus ergibt sich der Abstand \(d(M;F)\) des Mittelpunkts \(M\) der Kugel von der Ebene \(F\) wie folgt:
\(M(\textcolor{#e9b509}{0}|\textcolor{#e9b509}{0}|\textcolor{#e9b509}{4})\)
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[\begin{align*} d(M;F) &= \left|\frac{m_{1} + m_{2} - 2m_{3} + 2}{\sqrt{6}} \right| \\[0.8em] &= \left| \frac{\textcolor{#e9b509}{0} + \textcolor{#e9b509}{0} - 2 \cdot \textcolor{#e9b509}{4} + 2}{\sqrt{6}}\right| \\[0.8em] &= \left| \frac{-6}{\sqrt{6}}\right| = \sqrt{6} = r \end{align*}\]
(vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene)
Durchmesser der Marmorkugel auf Zentimeter genau berechnen:
Eine Längeneinheit entspricht einem Dezimeter (vgl. Angabe).
\(d = 2 \cdot r = 2 \cdot \sqrt{6}\,\text{dm} = 2 \cdot \sqrt{6} \cdot 10\,\text{cm} \approx 49\,\text{cm}\)
2. Möglichkeit: Abstand Punkt - Ebene, Lotfußpunktverfahren
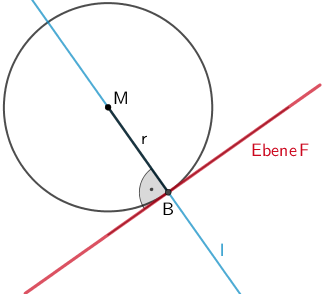
Planskizze (optional): Die Lotgerade \(\textcolor{#0087c1}{l}\) auf die Ebene \(F\) durch den Mittelpunkt \(M\) schneidet die Ebene \(F\) im Berührpunkt \(B\) (B ist Lotfußpunkt des Lotes von M auf F).
Es gilt: \(r = \vert \overrightarrow{MB} \vert\).
Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) formulieren:
Der Normalenvektor \(\textcolor{#0087c1}{\overrightarrow{n} = \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}}\) der Ebene \(F\) ist ein Richtungsvektor der Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) in Parameterform. Mit \(M(0|0|4) \in l\) folgt:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[\begin{align*} \textcolor{#0087c1}{l} \colon \overrightarrow{X} &= \overrightarrow{M} + \lambda \cdot \textcolor{#0087c1}{\overrightarrow{n}}; \lambda \in \mathbb R \\[0.8em] \textcolor{#0087c1}{l} \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + \lambda \cdot \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}}; \; \lambda \in \mathbb R\end{align*}\]
Koordinaten des Berührpunkts \(B\) bestimmen:
Hierfür werden die Koordinaten des Ortsvektors \(X\) der Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) in die Gleichung der Ebene \(\textcolor{#cc071e}{F}\) eingesetzt und diese nach dem Parameter \(\lambda\) aufgelöst.
\[\textcolor{#0087c1}{l} \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + \lambda \cdot \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}} = \textcolor{#0087c1}{\begin{pmatrix} \lambda \\ \lambda \\ 4 - 2\lambda \end{pmatrix}}\]
\[\textcolor{#cc071e}{F}\colon x_{1} + x_{2} - 2x_{3} + 2 = 0\]
\[\begin{align*} \textcolor{#0087c1}{l} \cap \textcolor{#cc071e}{F}\colon \textcolor{#0087c1}{\lambda} + \textcolor{#0087c1}{\lambda} - 2 \cdot (\textcolor{#0087c1}{4 - 2\lambda}) + 2 &= 0 \\[0.8em] 2\lambda - 8 + 4\lambda + 2 &= 0 \\[0.8em] 6\lambda - 6 &= 0 &&| + 6 \\[0.8em] 6\lambda &= 6 &&| : 6 \\[0.8em] \lambda &= 1 \end{align*}\]
Um den Ortsvektor \(\overrightarrow{B}\) des Berührpunkts zu ermitteln, wird der Parameterwert \(\textcolor{#e9b509}{\lambda = 1}\) in die Gleichung der Lotgerade \(\textcolor{#0087c1}{l}\) eingesetzt.
\[B \in \textcolor{#0087c1}{l}\colon \overrightarrow{B} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + \textcolor{#e9b509}{1} \cdot \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\]
Durchmesser der Marmorkugel auf Zentimeter genau berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}d &= 2 \cdot r = 2 \cdot \vert \overrightarrow{MB} \vert = 2 \cdot \vert \overrightarrow{B} - \overrightarrow{M}\vert \\[0.8em] &= 2 \cdot \left|\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} -\begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} \right| = 2 \cdot \left| \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}\right| \\[0.8em] &= 2 \cdot \sqrt{1^{2} + 1^{2} + (-2)^{2}} = 2\sqrt{6}\end{align*}\]
Eine Längeneinheit entspricht einem Dezimeter (vgl. Angabe).
\[d = 2\sqrt{6}\,\text{dm} = 2\sqrt{6} \cdot 10\,\text{cm} \approx 49\,\text{cm}\]


