Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen Definitionsmenge die angegebenen Eigenschaften besitzt.
Der Graph der Funktion \(f\) ist achsensymmetrisch zur \(y\)-Achse und die Gerade mit der Gleichung \(x = 2\) ist eine senkrechte Asymptote.
(2 BE)
Lösung zu Teilaufgabe 3a
Asymptoten gebrochenrationaler Funktionen, Symmetrieverhalten
Anmerkung:
Der Funktionsterm der gesuchten Funktion \(f\) ist lediglich anzugeben. Jede Erklärung kann entfallen.
1. Möglichkeit: Gebrochenrationale Funktion
Beispielsweise erfüllen die Graphen folgender gebrochenrationaler Funktionsterme die angegebenen Eigenschaften:
\(f(x) = \dfrac{1}{(x - 2)(x + 2)}\quad\) bzw. \(\quad f(x) = \dfrac{1}{x^{2} - 4}\)
oder
\(f(x) = \dfrac{x^{2}}{(x - 2)(x + 2)} \quad\) bzw. \(\quad f(x) = \dfrac{x^{2}}{x^{2} - 4}\)
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{p(x)}{q(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(p(x)\) und \(q(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(q(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Erklärung:
Wegen der geforderten Achsensymmetrie bzgl. der \(y\)-Achse ist die Gerade mit der Gleichung \(x = -2\) ebenfalls senkrechte Asymptote des Graphen der gesuchten Funktion \(f\).
Eine gebrochenrationale Funktion besitzt an einer Polstelle eine senkrechte Asymptote. Eine Polstelle liegt bei einer gebrochenrationalen Funktion im wesentlichen immer dann vor, wenn eine Nennernullstelle nicht zugleich Zählernullstelle ist.
Folglich müssen \(x = -2\) und \(x = 2\) Nullstellen des Nenners der gebrochenrationalen Funktion sein. Damit ergibt sich der Nennerterm beispielsweise zu: \((x - 2)((x + 2))\). Mithilfe der 3. binomischen Formel lässt sich der Nennerterm auch in der Form \(x^{2} - 4\) formulieren.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
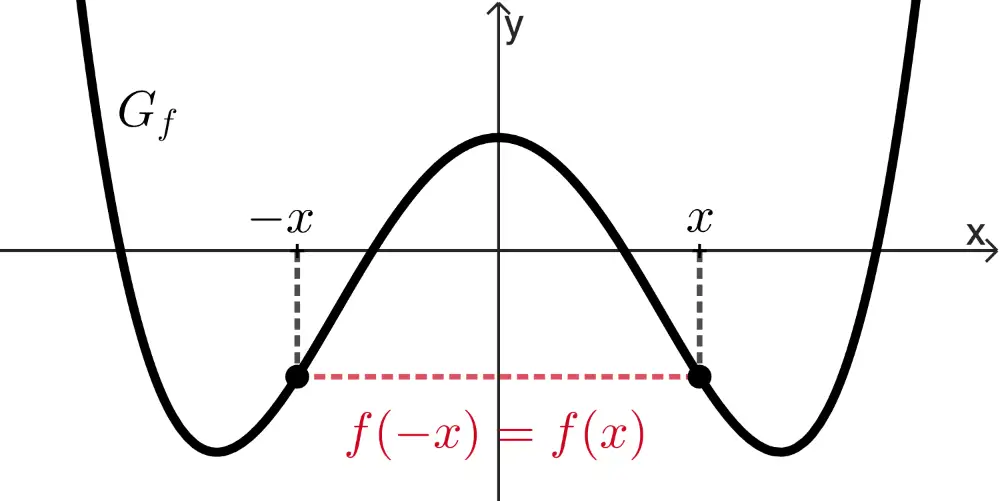
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
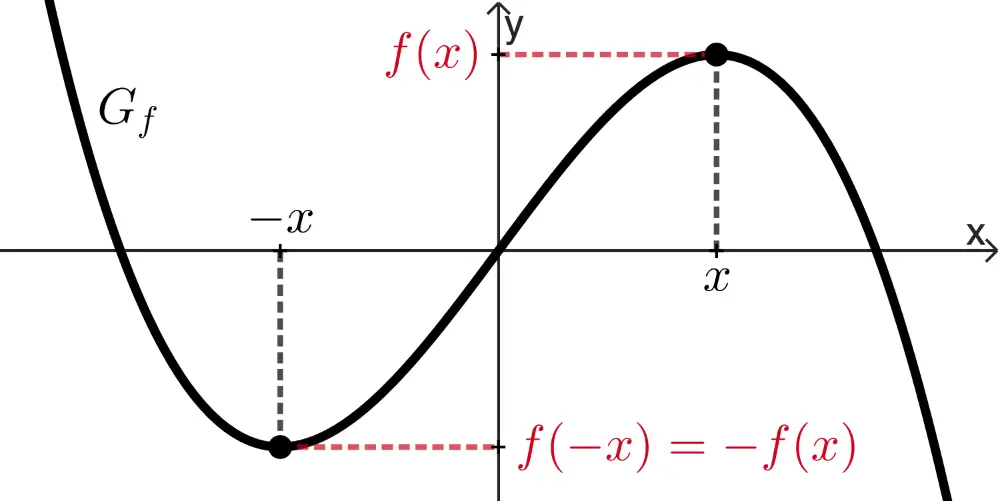
Der Zählerterm ist nun so zu beschreiben, dass die Achsensymmetrie bzgl. der \(y\)-Achse erhalten bleibt. Dies ist dann der Fall, wenn für die gesuchte Funktion \(f\) gilt: \(f(-x) = f(x)\). Da der Nennerterm \((x - 2)(x + 2) = x^{2} - 4\) für \(-x\) das Vorzeichen nicht ändert, darf auch der Zählerterm das Vorzeichen nicht ändern. Der Zählerterm kann somit beispielsweise eine Konstante sein, aber auch \(x^{2}\) kommt in Frage.
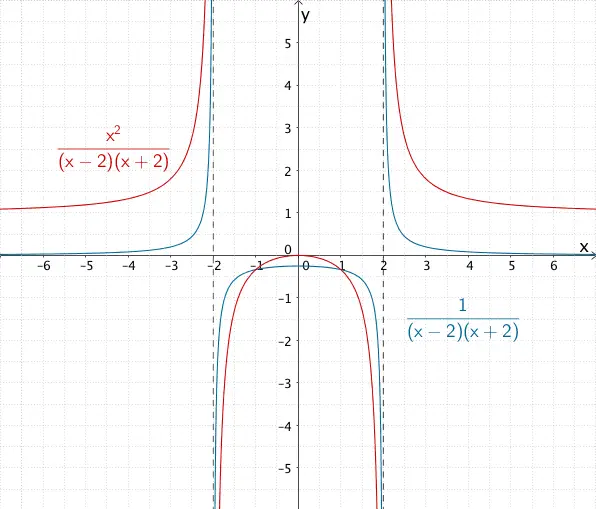
Zur \(y\)-Achse symmetrische Graphen der gebrochnrationalen Funktionen \(x \mapsto \dfrac{1}{(x - 2)(x + 2)}\) und \(x \mapsto \dfrac{x^{2}}{(x - 2)(x + 2)}\) mit den senkrechten Asymptoten \(x = -2\) und \(x = 2\)
2. Möglichkeit: Zusammengesetzte Logarithmusfunktion
Eine senkrechte Asymptote kennt man auch vom Graphen der in \(\mathbb R^{+}\) definierten natürlichen Logarithmusfunktion \(x \mapsto \ln{x}\).
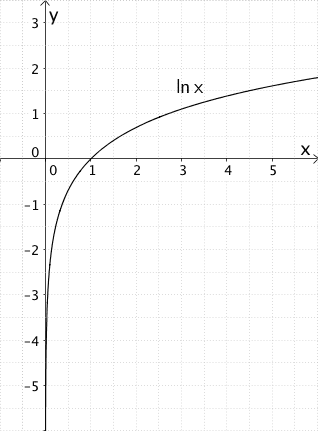
Mit \(\lim \limits_{x \,\to\, 0} \ln{x} = -\infty\) besitzt der Graph der in \(\mathbb R^{+}\) definierten natürlichen Logarithmusfunktion \(x \mapsto \ln{x}\) die senkrechte Asymptote mit der Gleichung \(x = 0\) (\(y\)-Achse).
Der Ansatz für die gesuchte Funktion \(f\) könnte beispielsweise lauten:
\(f(x) = \ln{\vert g(x) \vert}\)
Der Betrag von \(g(x)\) stellt sicher, dass die Funktion \(f\) nur an den Nullstellen von \(g\) nicht definiert ist. Damit der Graph der Funktion \(f\) die senkrechte Asymptote mit der Gleichung \(x = 2\) hat, muss \(x = 2\) eine Nullstelle von \(g\) sein. Wegen der geforderten Achsensymmetrie bezüglich der \(y\)-Achse des Graphen der Funktion \(f\), muss auch \(x = -2\) eine Nullstelle von \(g\) sein.
\(\Longrightarrow \quad\)z.B.: \(g(x) = (x - 2)(x + 2) = x^{2} - 4\)
Somit erfüllt beispielsweise der Graph der folgenden zusammengesetzten Logrithmusfunktion \(f\) die angegebenen Eigenschaften:
\[f(x) = \ln{\left(\vert x^{2} - 4 \vert\right)}\]
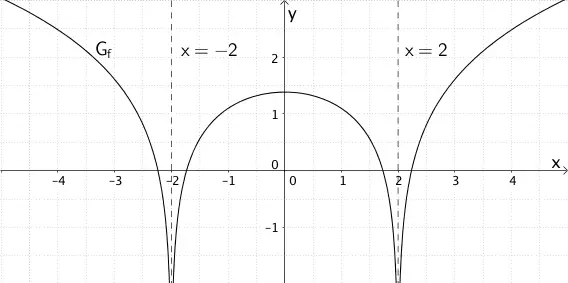
Bezüglich der \(y\)-Achse symmetrischer Graph \(G_{f}\) der zusammengesetzten natürlichen Logarithmusfunktion \(f \colon x \mapsto \ln\left( \vert x^{2} - 4 \vert \right)\) und den senkrechten Asymptoten \(x = 2\) und \(x = -2\)


