\(G_{f}\) geht aus dem Graphen der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto \frac{1}{18} \cdot (x^{3} - 25x)\) durch Verschiebung in positive \(x\)-Richtung hervor. Ermitteln Sie, um wie viel der Graph von \(g\) dazu verschoben werden muss. Begründen Sie mithilfe der Funktion \(g\), dass der Graph von \(f\) symmetrisch bezüglich seines Wendepunkts ist.

(4 BE)

Lösung zu Teilaufgabe 1c

 

Ermittlung der Verschiebung von \(G_{g}\)

Mithilfe der 3. Binomischen Formel lässt sich der Funktionsterm \(g(x)\) in seiner vollständig faktorisierten Form beschreiben. Daraus können die Nullstellen von \(g\) abgelesen und mit der Lage der Nullstellen der Funktion \(f\) verglichen werden. 

 

\[\begin{align*}g(x) &= \frac{1}{18} \cdot (x^{3} - 25x) &&| \; x\;\text{ausklammern} \\[0.8em] &= \frac{1}{18} \cdot x(\underbrace{x^{2} - 25}_{\Large{a^{2}\,-\,b^{2}}}) &&| \;\text{3. Binom. Formel anwenden} \\[0.8em] &= \frac{1}{18} \cdot x\underbrace{(x - 5)(x + 5)}_{\Large{(a\,-\,b)(a\,+\,b)}} \end{align*}\]

 

Also sind \(x = -5\), \(x = 0\) und \(x = 5\) Nullstellen von \(g\).

 

Veranschaulichung: Entstehung des Graphen der Funktion f aus dem Graphen der Funktion g durch Verschiebung um 5 LE in Richtung der positiven x-Achse

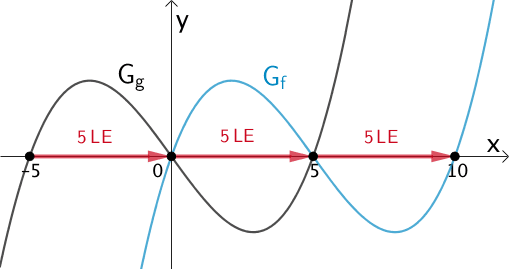
Ein Vergleich der Nullstellen von \(g\) mit den Nullstellen von \(f\) zeigt, dass \(G_{f}\) durch eine Verschiebung um 5 LE in positive \(x\)-Richtung aus dem Graphen \(G_{g}\) hervorgeht.

 

Begründung, dass \(G_{f}\) symmetrisch bezüglich seines Wendepunkts ist

Da \(g(x)\) ausschließlich ungerade Potenzen enthält, ist \(G_{g}\) punktsymmetrisch zum Koordinatenursprung \((0|0)\). Folglich ist der um 5 LE in positive \(x\)-Richtung verschobene Graph \(G_{f}\) punktsymmetrisch zu seinem Wendepunkt \(W(5|0)\).

 

Als Alternative kann die Punktsymmetrie zum Koordinatenursprung von \(G_{g}\) am Funktionsterm \(g(x)\) nachgewiesen werden.

Symmetrie von Funktionsgraphen (bzgl. des Koordinatensystems)

Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems

Der Graph einer Funktion \(f\) ist

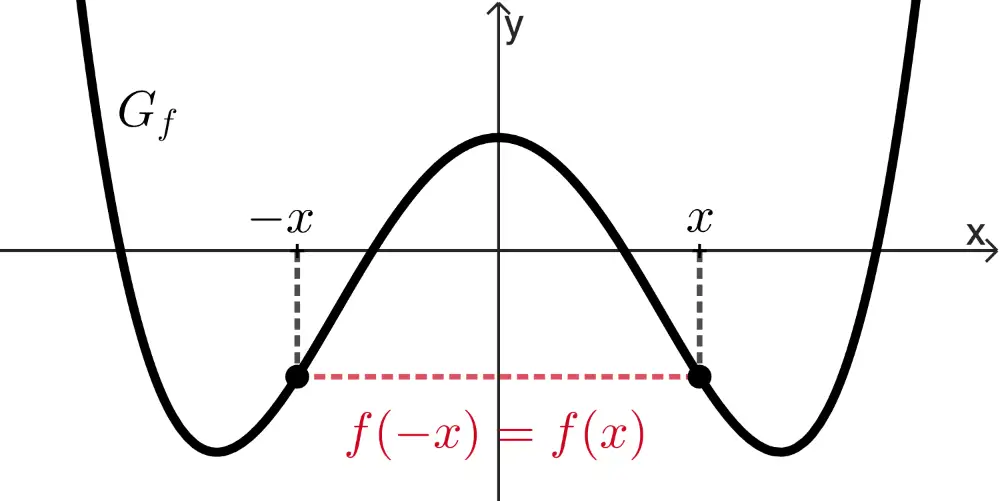
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).

Veranschaulichung der Symmetrie bezüglich der y-Achse

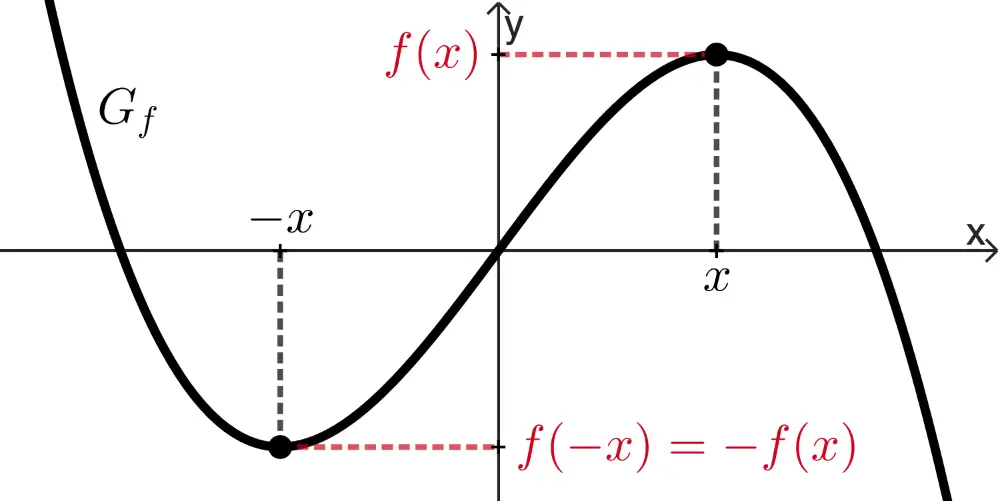
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)

Veranschaulichung der Symmetrie bezüglich des Koordinatenursprungs

\[\begin{align*}g(-x) &= \frac{1}{18} \cdot ((-x)^{3} - 25 \cdot (-x)) \\[0.8em] &= \frac{1}{18} \cdot (-x^{3} + 25x) \\[0.8em] &= -\frac{1}{18} \cdot (x^{3} - 25x) \\[0.8em] &= -g(x)\end{align*}\]

 

Also ist \(G_{g}\) punktsymmetrisch zum Koordinatenursprung und der um 5 LE in positive \(x\)-Richtung verschobene Graph \(G_{f}\) ist punktsymmetrisch zu seinem Wendepunkt \(W(5|0)\).