Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(\mathbb W\) hat.
\(\mathbb W = [2; + \infty[\)
(2 BE)
Lösung zu Teilaufgabe 2a
Terme von Potenzfunktionen \(f\) mit geraden Exponenten \(n\) und einer Verschiebung um \(2\) in \(y\)-Richtung sind in \(\mathbb R\) definiert und haben die Wertemenge \(\mathbb W = [2;+ \infty[\).
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[f(x) = x^n + 2\,; \quad n = 2k\,; \quad k \in \mathbb N\]
Beispiele:
\[f_1(x) = x^2 + 2\]
\[f_2(x) = x^4+2\]
\[f_3(x)=x^{10}+2\]
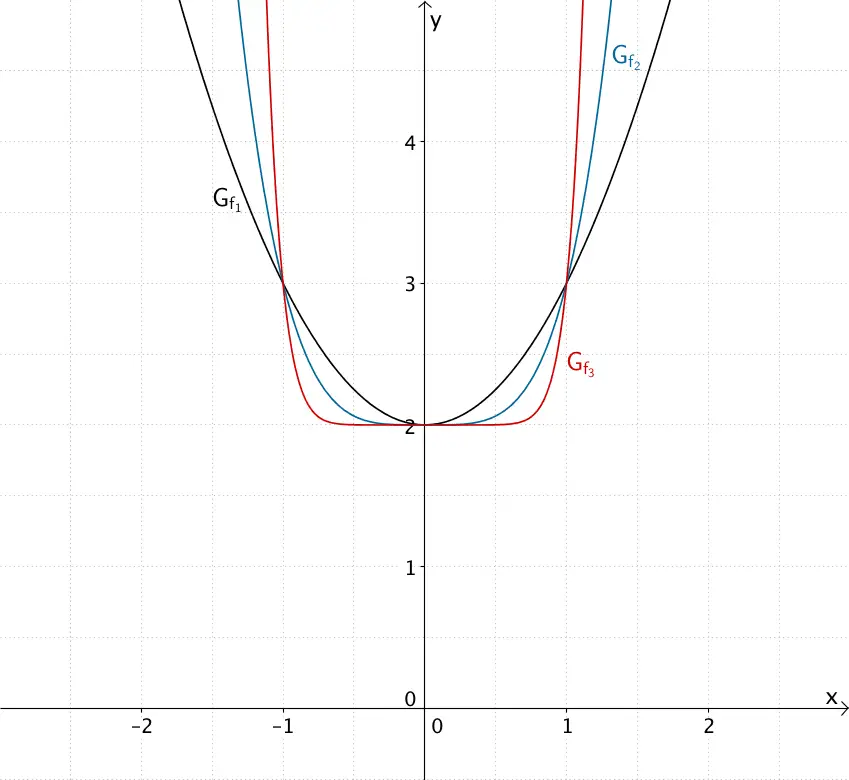
Graphen der in \(\mathbb R\) definierten Potenzfunktionen \(f_1\), \(f_2\) und \(f_3\) mit der Wertemenge \(\mathbb W = [2;+\infty[\)


