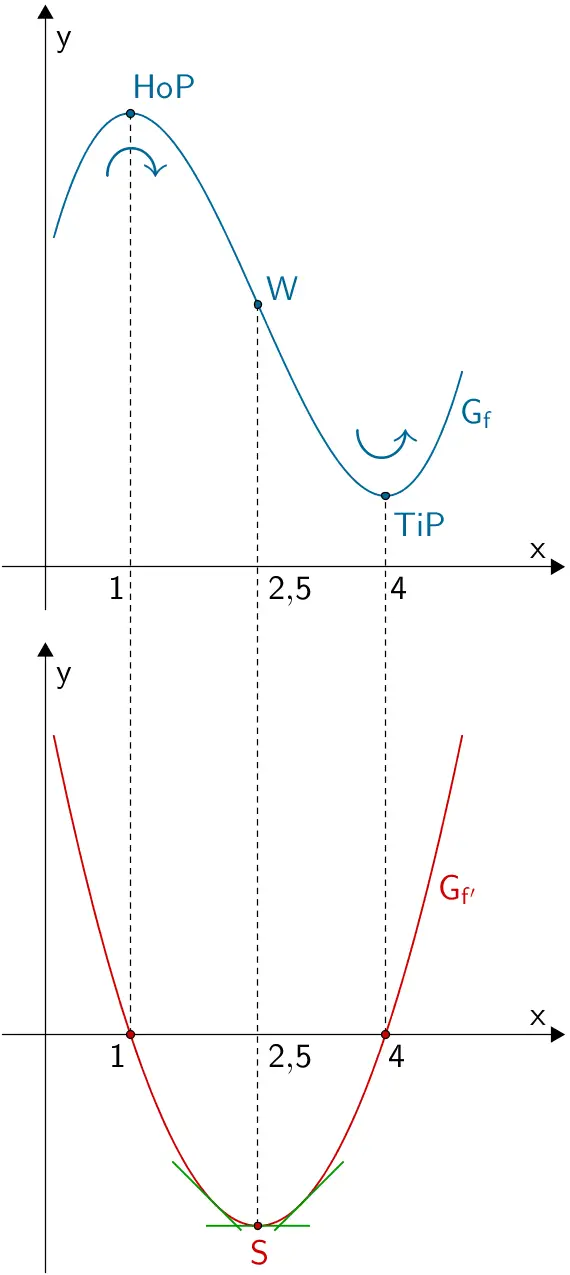
Begründen Sie, dass \(2{,}5\) die \(x\)-Koordinate des Wendepunkts von \(G_{f}\) ist.

(2 BE)

Lösung zu Teilaufgabe 4b

Graph der Ableitung einer Funktion analysieren

Die Extremstellen des Graphen der Ableitung einer Funktion sind die Wendestellen des Graphen der Funktion. Denn an den Wendestellen ist die Steigung des Graphen einer Funktion (Steigung der Wendetangente), abhängig vom Wechsel der Graphenkrümmung, entweder maximal oder minimal.

Die Parabel von \(f'\) hat genau einen Extrempunkt, den Scheitelpunkt \(S\). Durch den Scheitelpunkt verläuft die Symmetrieachse der Parabel. Die Symmetrieachse \(x = x_{S}\) lässt sich anhand der bekannten Nullstellen \(x_{1} = 1\) und \(x_{2} = 4\) der Parabel von \(f'\) bestimmen.

\[x_{S} = \frac{x_{1} + x_{2}}{2} = \frac{1 + 4}{2} = \frac{5}{2} = 2{,}5\]

oder

\[x_{S} = x_{1} + \frac{x_{2} - x_{1}}{2} = 1 + \frac{4 - 1}{2} = 1 + 1{,}5 = 2{,}5\]

\(\Longrightarrow \quad x = 2{,}5\) ist Symmetrieachse der Parabel von \(f'\).

Damit ist 2,5 die \(x\)-Koordinate des Scheitel- und Extrempunkts der Parabel von \(f'\) und folglich auch die \(x\)-Koordinate des Wendepunkts von \(G_{f}\).

An der Extremstelle \(x = 2{,}5\) besitzt die Parabel von \(f'\) eine waagrechte Tangente (Tangentensteigung ist gleich Null) und es gilt folglich \(f''(2{,}5) = 0\). Zudem wechselt die Steigung einer Tangente an die Parabel in der Umgebung der Extremstelle das Vorzeichen, was einem Vorzeichenwechsel von \(f''\) entspricht. Damit sind die Bedingungen für einen Wendepunkt des Graphen der Funktion \(f\) an der Stelle \(x = 2{,}5\) erfüllt.