Von den Eckpunkten des Rechtecks \(ABCD\) liegen der Punkt \(A(s|0)\) mit \(s \in \;]0;5[\) sowie der Punkt \(B\) auf der \(x\)-Achse, die Punkte \(C\) und \(D\) liegen auf \(G_f\). Das Rechteck besitzt somit die Gerade mit der Gleichung \(x = 5\) als Symmetrieachse. Zeigen Sie, dass die Diagonalen dieses Rechtecks jeweils die Länge 10 besitzen.
(5 BE)
Lösung zu Teilaufgabe h
![Rechteck ABCD mit A(s|0) (s ∈ ]0;5[), B(10 - s|0), C(10 - s|f(s)) und D(s|f(s)), Rechtwinkliges Dreieck ABC](/images/stories/B2022_PT_B_A1/B2022_PT_B_A1_h.png)
Planskizze (optional): Aus Symmetriegründen (vgl. Angabe) ergibt sich \(\textcolor{#cc071e}{B(10 - s|0)}\).
Die Länge der Seite \(\textcolor{#cc071e}{[AB]}\) ist gleich der Differenz der \(\textcolor{#cc071e}{x}\)-Koordinaten der Punkte \(\textcolor{#cc071e}{A}\) und \(\textcolor{#cc071e}{B}\).
Da der Punkt \(\textcolor{#cc071e}{C}\) vertikal über Punkt \(\textcolor{#cc071e}{B}\) auf \(G_f\) liegt, gilt: \(\textcolor{#cc071e}{\overline{BC} = f(s)}\).
Die Diagonale \(\textcolor{#cc071e}{[AC]}\) des Rechtecks \(ABCD\) ist die Hypotenuse des rechtwinkligen Dreiecks \(\textcolor{#cc071e}{ABC}\).
Mithilfe des Satzes des Pythagoras folgt:
\(A(\textcolor{#cc071e}{s}|0)\), \(B(\textcolor{#cc071e}{10 - s}|0)\), \(C(10 - s|\textcolor{#cc071e}{f(s)})\)
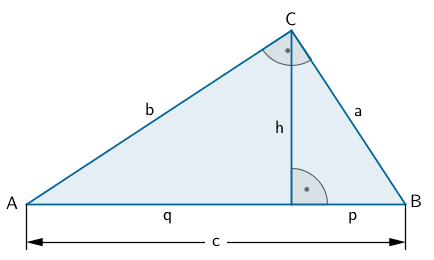
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} {\textcolor{#cc071e}{\overline{AC}}}^2 &= {\textcolor{#cc071e}{\overline{AB}}}^2 + {\textcolor{#cc071e}{\overline{BC}}}^2 \\[0.8em] {\textcolor{#cc071e}{\overline{AC}}}^2 &= (\textcolor{#cc071e}{(10 - s) - s})^2 + [\textcolor{#cc071e}{f(s)}]^2 &&|\; f(x) = 2 \cdot \sqrt{10x - x^2} \\[0.8em] \textcolor{#cc071e}{\overline{AC}} &= \sqrt{(\textcolor{#cc071e}{10 - 2s})^2 + (\textcolor{#cc071e}{2 \cdot \sqrt{10s - s^2}})^2} &&|\; \text{2. Bin. Formel anwenden} \\[0.8em] &= \sqrt{100 - 40s + 4s^2 + 4 \cdot (10s - s^2)} \\[0.8em] &= \sqrt{100 - 40s + 4s^2 + 40s - 4s^2} \\[0.8em] &= \sqrt{100} \\[0.8em] &= 10 \end{align*}\]
Da die Diagonalen eines Rechtecks gleichlang sind, gilt: \(\overline{AC} = \overline{BD} = 10\).


