Die Grundplatte ist gegenüber der Horizontalen um den Winkel \(\alpha\) geneigt. Damit man mit der Sonnenuhr die Uhrzeit korrekt bestimmen kann, muss für den Breitengrad \(\varphi\) des Aufstellungsorts der Sonnenuhr \(\alpha + \varphi = 90^{\circ}\) gelten. Bestimmen Sie, für welchen Breitengrad \(\varphi\) die Sonnenuhr gebaut wurde.
(4 BE)
Lösung zu Teilaufgabe b
Schnittwinkel zweier Ebenen
\[\alpha + \varphi = 90^{\circ}\]
Neigungswinkel \(\alpha\) der Grundplatte gegenüber der Horizontalen:
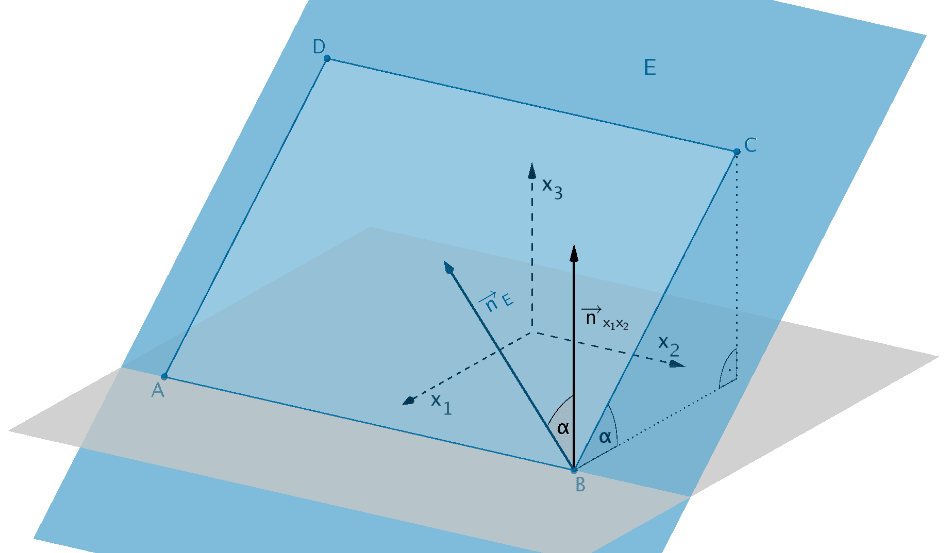
Das Rechteck \(ABCD\), welches die Grundplatte beschreibt, liegt in der Ebene \(E\). Folglich ist der Neigungswinkel \(\alpha\) der Grundplatte gegenüber der Horizontalen gleich dem Schnittwinkel zwischen der Ebene \(E\) und der \(x_{1}x_{2}\)-Ebene.
Der Schnittwinkel \(\alpha\) zwischen der Ebene \(E\) und der \(x_{1}x_{2}\)-Ebene ist gleich dem Winkel zwischen dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und dem Normalenvektor \(\overrightarrow{n}_{x_{1}x_{2}}\) der \(x_{1}x_{2}\)-Ebene (zur besseren Darstellung verlängert gezeichnet).
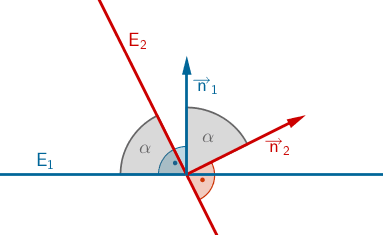
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_{E} \circ \overrightarrow{n}_{x_{1}x_{2}} \vert}{\vert \overrightarrow{n}_{E} \vert \cdot \vert \overrightarrow{n}_{x_{1}x_{2}} \vert}\]
Normalenvektor der \(x_{1}x_{2}\)-Ebene:
\[x_{1}x_{2} \text{-Ebene}\colon x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Neigungswinkel (Schnittwinkel) \(\alpha\) berechnen:
\[\begin{align*} \cos \alpha &= \frac{\vert \overrightarrow{n}_{E} \circ \overrightarrow{n}_{x_{1}x_{2}} \vert}{\vert \overrightarrow{n}_{E} \vert \cdot \vert \overrightarrow{n}_{x_{1}x_{2}} \vert} \\[0.8em] &=\frac{\left| \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{4 \cdot 0 + 0 \cdot 0 + 5 \cdot 1}{\sqrt{4^{2} + 0^{2} + 5^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{5}{\sqrt{41} \cdot \sqrt{1}} \\[0.8em] &= \frac{5}{\sqrt{41}} \\[0.8em] &= \frac{5\sqrt{41}}{41} \end{align*}\]
\[\alpha \approx 38{,}66^{\circ}\]
Breitengrad \(\varphi\) berechnen:
\[\begin{align*}\alpha + \varphi = 90^{\circ} \quad \Longleftrightarrow \quad \varphi &= 90^{\circ} - \alpha \\[0.8em] &= 90^{\circ} - 38{,}66^{\circ} \\[0.8em] &= 51{,}34^{\circ} \end{align*}\]
Die Sonnenuhr wurde für den Breitengrad 51,34 ° gebaut.