Geben Sie den Term einer gebrochenrationalen Funktion \(f\) an,
- deren Graph die senkrechten Asymptoten mit den Gleichungen \(x = -2\) und \(x = 3\), die doppelte Nullstelle \(x = 1\) sowie die waagrechte Asymptote mit der Gleichung \(y = 0\) besitzt.
- die in \(\mathbb R\) definiert ist und deren Graph die waagrechte Asymptote mit der Gleichung \(y = 1\) besitzt sowie die \(y\)-Achse bei \(3\) schneidet.
a) Funktionsterm einer gebrochenrationalen Funktion \(f\)
mit den Eigenschaften:
- Der Graph von \(f\) besitzt die senkrechten Asymptoten mit den Gleichungen \(x = -2\) und \(x = 3\).
- \(f\) hat die doppelte Nullstelle \(x = 1\).
- Der Graph von \(f\) besitzt die waagrechte Asymptote mit der Gleichung \(y = 0\).
Beispielsweise: \(f(x) = \dfrac{(x-1)^2}{x(x+2)(x-3)}, \;D_f = \mathbb R \backslash \{-2;0;3\}\)
Ergänzende Erklärung (nicht verlangt)
Ansatz: \(f(x) = \dfrac{p(x)}{q(x)}\), wobei \(p(x)\) das Zählerpolynom und \(q(x)\) das Nennerpolynom ist.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{p(x)}{q(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(p(x)\) und \(q(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(q(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
1. Der Graph von \(f\) besitzt die senkrechten Asymptoten mit den Gleichungen \(\textcolor{#0087c1}{x = -2}\) und \(\textcolor{#0087c1}{x = 3}\)
An einer Polstelle besitzt der Graph einer gebrochenrationalen Funktion eine senkrechte Asymptote. Polstellen sind Nullstellen des Nennerpolynoms \(q(x)\) (Definitionslücken), die nicht zugleich Nullstellen des Zählerpolynoms \(p(x)\) sind.
\[\Rightarrow \; \frac{p(x)}{\textcolor{#0087c1}{(x+2)(x-3)}}\]
2. \(f\) hat die doppelte Nullstelle \(\textcolor{#cc071e}{x = 1}\)
Die Nullstellen des Zählerpolynoms \(p(x)\) sind die Nullstellen der gebrochenrationalen Funktion \(f\). Bei einer doppelten Nullstelle ist der zugehörige Linearfaktor vom Grad 2.
\[\Rightarrow \; \frac{\textcolor{#cc071e}{(x-1)^2}}{\textcolor{#0087c1}{(x+2)(x-3)}}\]
3. Der Graph von \(f\) besitzt die waagrechte Asymptote mit der Gleichung \(y = 0\).
Wenn der Zählergrad \(z\) kleiner ist als der Nennergrad \(n\), besitzt der Graph einer gebrochenrationalen Funktion die \(x\)-Achse mit der Gleichung \(y = 0\) als waagrechte Asymptote für das Verhalten im Unendlichen.
Deshalb wird der Zähler im einfachsten Fall um den Faktor \(\textcolor{#0087c1}{x}\) erweitert.
\(\Rightarrow \; f(x) = \dfrac{\textcolor{#cc071e}{(x-1)^2}}{\textcolor{#0087c1}{x(x+2)(x-3)}} = \dfrac{x^2 - \cdots}{x^3 + \cdots}\enspace (z < n)\)
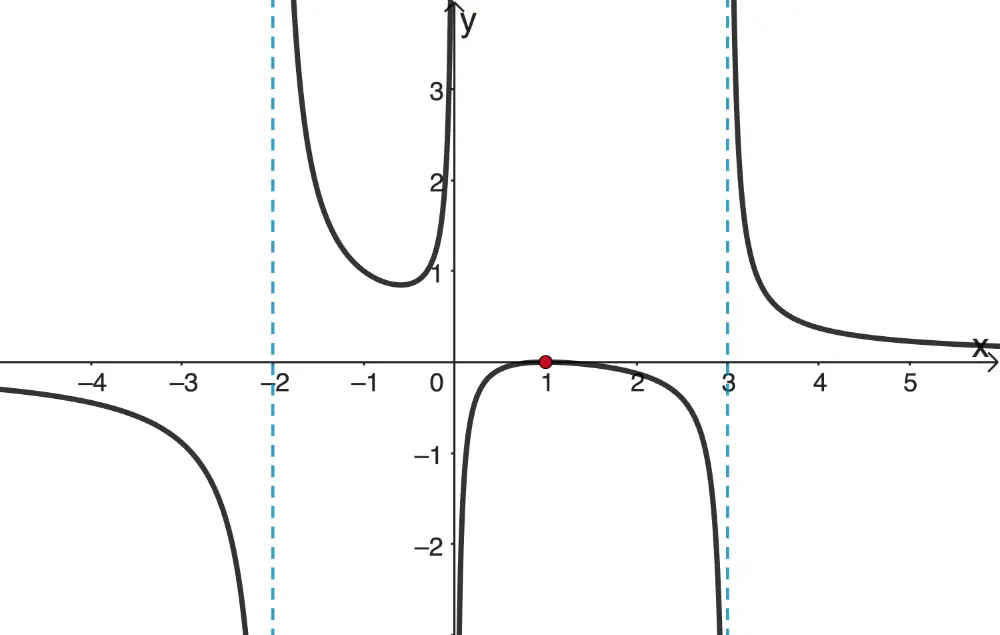
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{(x-1)^2}{x(x+2)(x-3)}\) (ergänzende Zeichnung)
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.2 Gebrochenrationale Funktion - Funktionsbestimmungen)
b) Funktionsterm einer gebrochenrationalen Funktion \(f\)
mit den Eigenschaften:
- \(f\) ist in \(\mathbb R\) definiert.
- Der Graph von \(f\) besitzt die waagrechte Asymptote mit der Gleichung \(y = 1\).
- Der Graph von \(f\) schneidet die \(y\)-Achse bei \(3\).
Beispielsweise: \(f(x) = \dfrac{x^2+3}{x^2+1}, \; D_f = \mathbb R\)
oder \(f(x) = \dfrac{2}{x^2+1} + 1, \; D_f = \mathbb R\)
Ergänzende Erklärung (nicht verlangt)
Ansatz: \(f(x) = \dfrac{p(x)}{q(x)}\), wobei \(p(x)\) das Zählerpolynom und \(q(x)\) das Nennerpolynom ist.
1. \(f\) ist in \(\mathbb R\) definiert.
Das Nennerpolynom \(p(x)\) darf keine Nullstelle besitzen. Diese Bedingung erfüllt z. B. der Term \(x^2 + 1\) mit \(x^2 + 1 > 0\) für alle \(x \in \mathbb R\)
\[\Rightarrow \; \frac{p(x)}{x^2+1}\]
2. Der Graph von \(f\) besitzt die waagrechte Asymptote mit der Gleichung \(y = 1\).
Der Graph einer gebrochenrationalen Funktion besitzt eine waagrechte Asymptote mit der Gleichung \(y = c, \; c \in \mathbb R \backslash \{0\}\), wenn der Zählergrad \(z\) gleich dem Nennergrad \(n\) ist. Der Wert von \(c\) ergibt sich durch den Quotienten der Leitkoeffizienten des Zähler- bzw. Nennerpolynoms (Faktoren der höchsten Potenzen).
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{p(x)}{q(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(p(x)\) und \(q(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(q(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\(\Rightarrow \; \dfrac{\textcolor{#cc071e}{1} \cdot x^2}{\textcolor{#0087c1}{1} \cdot x^2 + 1} \enspace (z = n)\)
Gleichung der waagrechten Asymptote: \(\smash{y = \dfrac{\textcolor{#cc071e}{1}}{\textcolor{#0087c1}{1}} = 1}\vphantom{\dfrac{x^2}{x^2}}\)
3. Der Graph von \(f\) schneidet die \(y\)-Achse bei \(3\).
Es muss \(f(0) = 3\) gelten. Hierfür wird das Zählerpolynom mit \(+3\) angepasst.
\[\Rightarrow \; f(x) = \frac{x^2+3}{x^2+1}, \; D_f = \mathbb R\]
Alternativer Ansatz: \(f(x) = r(x) + c\)
Dabei ist \(r(x)\) ein gebrochenrationaler Summand, der die Definitionsmenge bestimmt, also in \(\mathbb R\) definiert sein muss. Der Wert des Parameters \(c \in \mathbb R \backslash \{0\}\) legt mit \(\textcolor{#e9b509}{\lim \limits_{x\,\to\,\pm\infty}r(x) = 0}\) die Gleichung der waagrechten Asymptote fest.
\[\Rightarrow \; \frac{a}{x^2+1} + 1, \; a \in \mathbb R\]
\[\lim \limits_{x\,\to\,\pm\infty} \textcolor{#e9b509}{\underbrace{\frac{a}{x^2+1}}_{\to\,0}} + 1 = 1\]
Mit \(f(0) = 3\) folgt \(a = 2\).
\[\Rightarrow \; f(x) = \frac{2}{x^2+1} + 1\]
Anmerkung
Die Funktionsterme der beiden Lösungsansätze sind äquivalent.
\[f(x) = \frac{2}{x^2+1} + 1 = \frac{2}{x^2+1} + \frac{x^2+1}{x^2+1} = \frac{x^2+3}{x^2+1}\]

Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \dfrac{x^2+3}{x^2+1}\) (ergänzende Zeichnung)


