Gleichung einer Gerade in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) der Richtungsvektor der Gerade \(g\).
Eine Gerade wird durch folgende Angaben eindeutig festgelegt:
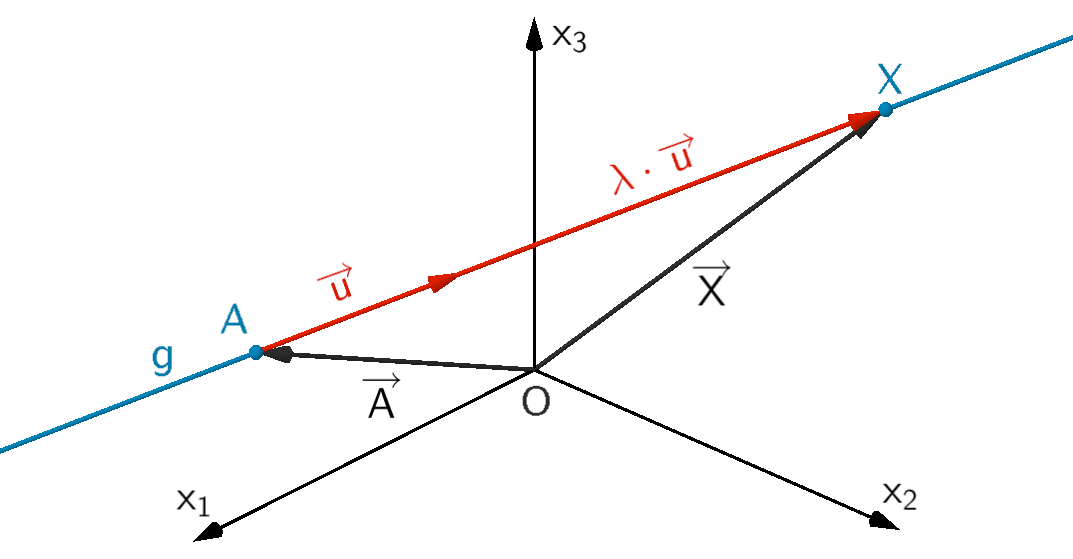
Ein Punkt \(A\) und ein Vektor \(\overrightarrow{u}\)
Punkt-Richtung-Form
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\]
Zwei Punkte \(A\) und \(B\)
Zwei-Punkte-Form
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\]
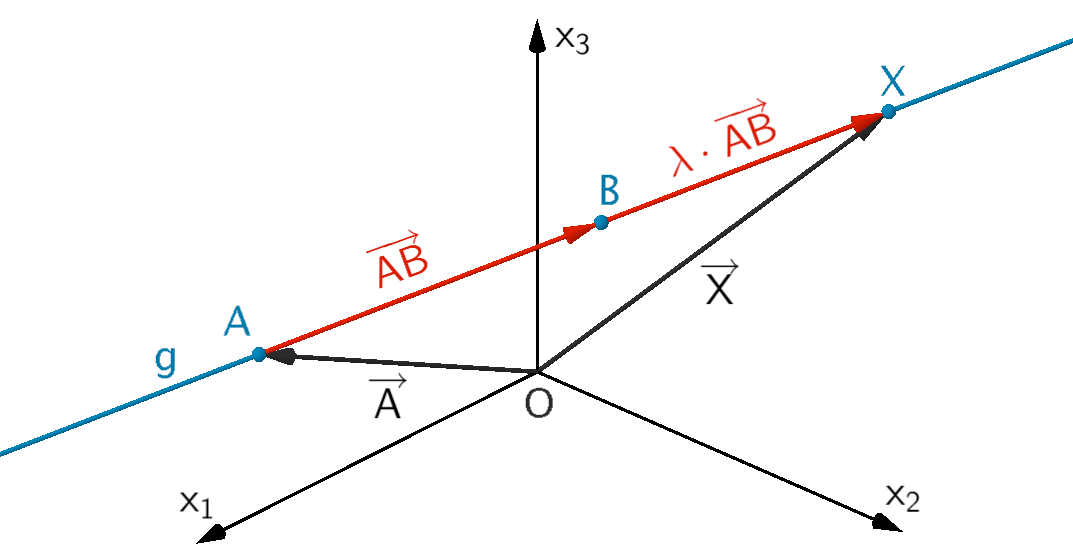
Zu jedem Wert des Parameters \(\lambda\) gehört genau ein Punkt \(X\) auf der Gerade \(g\). Als Aufpunkt \(A\) kann jeder Punkt der Gerade verwendet werden. Als Richtungsvektor der Gerade kommt jedes beliebige Vielfache des Vektors \(\overrightarrow{u}\) bzw. \(\overrightarrow{AB}\) in Frage. Die Gleichung einer Gerade in Parameterform ist also nicht eindeutig bestimmt.
Lage einer Gerade im Koordinatensystem
Will man die Lage einer Gerade bezüglich der Koordinatenachsen oder der Koordinatenebenen beschreiben, betrachtet man den Richtungsvektor der Gerade.
Parallelität einer Gerade zu einer Koordinatenachse
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\]
\[\overrightarrow{u} = k \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}; \enspace k \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{1}\text{-Achse}\]
\[\overrightarrow{u} = k \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \enspace k \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{2}\text{-Achse}\]
\[\overrightarrow{u} = k \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \enspace k \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{3}\text{-Achse}\]
Sind also zwei Vektorkoordinaten des Richtungsvektors einer Gerade gleich Null, so verläuft die Gerade parallel zu einer der Koordinatenachsen.
Parallelität einer Gerade zu einer Koordinatenebene
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\]
\[\overrightarrow{u} = \begin{pmatrix} u_{1} \\ u_{2} \\ 0 \end{pmatrix}; \enspace u_{1}, u_{2} \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{1}x_{2}\text{-Ebene}\]
\[\overrightarrow{u} = \begin{pmatrix} u_{1} \\ 0 \\ u_{3} \end{pmatrix}; \enspace u_{1}, u_{3} \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{1}x_{3}\text{-Ebene}\]
\[\overrightarrow{u} = \begin{pmatrix} 0 \\ u_{2} \\ u_{3} \end{pmatrix}; \enspace u_{2}, u_{3} \in \mathbb R \quad \Longrightarrow \quad g \parallel x_{2}x_{3}\text{-Ebene}\]
Ist also eine Vektorkoordinate des Richtungsvektors einer Gerade gleich Null, so verläuft die Gerade parallel zu einer der Koordinatenebenen.
Spurpunkte einer Gerade
Spurpunkte sind die Schnittpunkte einer Gerade mit den Koordinatenebenen. Anhand der Spurpunkte lässt sich die Lage einer Gerade im Koordinatensystem veranschaulichen.
Bestimmung der Spurpunkte einer Gerade
Eine Koordinate eines Spurpunkts einer Gerade ist gleich Null, da dieser in einer Koordinatenebene liegt. Sonderfall: Der Spurpunkt liegt auf einer Koordinatenachse. Dann sind zwei Koordinaten des Spurpunkts gleich Null.
Spurpunkt in der \(x_{1}x_{2}\)-Ebene: \(S_{x_{1}x_{2}}(s_{1}|s_{2}|0)\)
Spurpunkt in der \(x_{1}x_{3}\)-Ebene: \(S_{x_{1}x_{3}}(s_{1}|0|s_{3})\)
Spurpunkt in der \(x_{2}x_{3}\)-Ebene: \(S_{x_{2}x_{3}}(0|s_{2}|s_{3})\)
Damit lautet die Bedingung für einen Spurpunkt einer Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} + \lambda \cdot \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix}; \; \lambda \in \mathbb R\)
mit der \(x_{1}x_{2}\)-Ebene: \(a_{3} + \lambda \cdot u_{3} = 0\)
mit der \(x_{1}x_{3}\)-Ebene: \(a_{2} + \lambda \cdot u_{2} = 0\)
mit der \(x_{2}x_{3}\)-Ebene: \(a_{1} + \lambda \cdot u_{1} = 0\)
Existiert ein Spurpunkt mit einer Koordinatenebene, liefert die jeweilige Gleichung einen Wert für den Parameter \(\lambda\). Diesen setzt man in die Geradengleichung ein und erhält den Ortsvektor des jeweiligen Spurpunkts.
Beispiel:
Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\).
Bestimmen Sie die Spurpunkte der Gerade \(g\).
Spurpunkt der Gerade \(g\) mit der \(x_{1}x_{2}\)-Ebene
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix}\]
\[S_{x_{1}x_{2}}(s_{1}|s_{2}|0)\]
\[\begin{align*} \Longrightarrow \quad 3 + 2\lambda &= 0 & &| - 3 \\[0.8em] 2\lambda &= -3 & &| : 2 \\[0.8em] \lambda &= -\frac{3}{2} \end{align*}\]
Parameterwert \(\lambda = -\dfrac{3}{2}\) in die Gleichung der Geraden \(g\) einsetzen:
\[\overrightarrow{S}_{x_{1}x_{2}} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} - \frac{3}{2} \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix} = \begin{pmatrix} 8 \\ -5 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}x_{2}}(8|-5|0)\]
Spurpunkt der Gerade \(g\) mit der \(x_{1}x_{3}\)-Ebene
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix}\]
\[S_{x_{1}x_{3}}(s_{1}|0|s_{3})\]
\[\begin{align*} \Longrightarrow \quad 2{,}5 + 5\lambda &= 0 & &| - 2{,}5 \\[0.8em] 5\lambda &= -2{,}5 & &| : 5 \\[0.8em] \lambda &= -\frac{1}{2} \end{align*}\]
Parameterwert \(\lambda = -\dfrac{1}{2}\) in die Gleichung der Gerade \(g\) einsetzen:
\[\overrightarrow{S}_{x_{1}x_{3}} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} - \frac{1}{2} \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ 2 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}x_{2}}(4|0|2)\]
Spurpunkt der Gerade \(g\) mit der \(x_{2}x_{3}\)-Ebene
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix}\]
\[S_{x_{2}x_{3}}(0|s_{2}|s_{3})\]
\[\begin{align*} \Longrightarrow \quad 2 - 4\lambda &= 0 & &| + 4\lambda \\[0.8em] 2 &= 4\lambda & &| : 4 \\[0.8em] \frac{1}{2} &= \lambda \end{align*}\]
Parameterwert \(\lambda = \dfrac{1}{2}\) in die Gleichung der Gerade \(g\) einsetzen:
\[\overrightarrow{S}_{x_{2}x_{3}} = \begin{pmatrix} 2 \\ 2{,}5 \\ 3 \end{pmatrix} + \frac{1}{2} \cdot \begin{pmatrix} -4 \\ 5 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 5 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}x_{2}}(0|5|4)\]
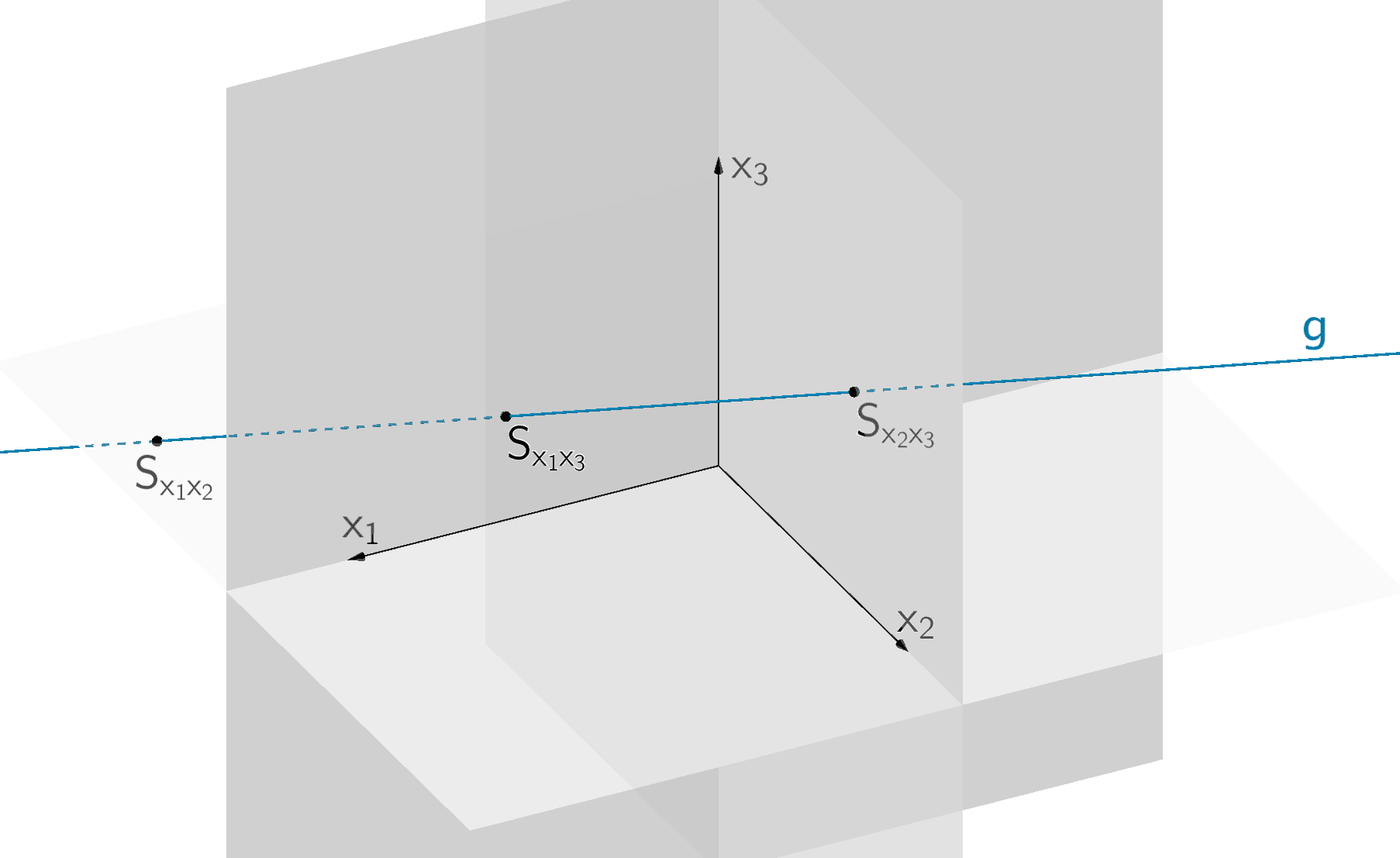
Spurpunkte der Gerade \(g\) mit den Koordinatenebenen
Beispielaufgabe
Gegeben seien die Punkte \(A(-4|3|-2)\), \(B(5|-5|3)\), \(C(14|-13|8)\) und \(D(-4|-8|-1)\).
Prüfen Sie, ob die Punkte \(C\) und \(D\) auf der Geraden durch die Punkte \(A\) und \(B\) liegen.
Man formuliert zunächst eine Gleichung der Gerade \(AB\) und überprüft anschließend, ob die Ortsvektoren der Punkte \(C\) und \(D\) die Geradengleichung erfüllen (Punktprobe).
Gleichung der Gerade \(AB\) in Parameterform
Als Aufpunkt für die Gleichung der Gerade \(AB\) wählt man beispielsweise den Punkt \(A\) und als Richtungsvektor den Verbindungsvektor \(\overrightarrow{AB}\).
\[AB \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}\,; \; \lambda \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{AB}\) berechnen:
\(A(-4|3|-2)\), \(B(5|-5|3)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 5 \\ -5 \\ 3 \end{pmatrix} - \begin{pmatrix} -4 \\ 3 \\ -2 \end{pmatrix} = \begin{pmatrix} 9 \\ -8 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad AB \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 3 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 9 \\ -8 \\ 5 \end{pmatrix}; \; \lambda \in \mathbb R\]
Prüfung, ob die Punkte \(C\) und \(D\) auf der Gerade \(AB\) liegen
\[AB \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 3 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 9 \\ -8 \\ 5 \end{pmatrix}\]
\(C(14|-13|8)\), \(D(-4|-8|-1)\)
\[C \in AB \colon \begin{pmatrix} 14 \\ -13 \\ 8 \end{pmatrix} = \begin{pmatrix} -4 \\ 3 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 9 \\ -8 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad \begin{cases} \enspace \; 14 = -4 + 9\lambda \quad \Longleftrightarrow \quad \enspace \; 18 = \enspace \; 9\lambda \quad \Longrightarrow \quad \lambda = 2 \\[0.8em] -13 = \enspace \; 3 - 8\lambda \quad \Longleftrightarrow \quad -16 = -8\lambda \quad \Longrightarrow \quad \lambda = 2 \\[0.8em] \quad \; 8 = -2 + 5\lambda \quad \Longleftrightarrow \quad \enspace \; 10 = \enspace \; 5\lambda \quad \Longrightarrow \quad \lambda = 2 \end{cases}\]
\(\Longrightarrow \quad C \in AB\) (Der Punkt \(C\) liegt auf der Geraden \(AB\).)
\[D \in AB \colon \begin{pmatrix} -4 \\ -8 \\ -1 \end{pmatrix} = \begin{pmatrix} -4 \\ 3 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 9 \\ -8 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad \begin{cases} -4 = -4 + 9\lambda \quad \Longleftrightarrow \qquad \; 0 = \enspace \; 9\lambda \quad \Longrightarrow \quad \lambda = 0 \\[0.8em] -8 = \enspace \; 3 - 8\lambda \quad \Longleftrightarrow \quad -11 = -8\lambda \quad \Longrightarrow \quad \lambda = \frac{11}{8} \\[0.8em] -1 = -2 + 5\lambda \quad \Longleftrightarrow \qquad \; 1 = \enspace \; 5\lambda \quad \Longrightarrow \quad \lambda = \frac{1}{5} \end{cases}\]
\(\Longrightarrow \quad\)Keine eindeutige Lösung für \(\lambda \quad \Longrightarrow \quad D \notin AB\)


