Bestimmen Sie rechnerisch den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.
(5 BE)
Lösung zu Teilaufgabe 1c
Gesucht ist der Zeitpunkt, zu dem die momentane Änderungsrate der Staulänge, beschrieben durch die Funktion \(f\), maximal ist.
Die notwendige Bedingung für ein Maximum von \(f\) lautet:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
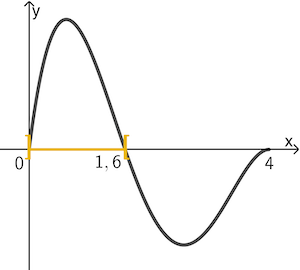Abb. 1
Unter Berücksichtigung der Nullstellen \(x = 0\) und \(x = 1{,}6\) von \(f\) (vgl. Teilaufgabe 1a) sowie Abbildung 1, kommen als sinnvolle Lösungen nur Werte \(\textcolor{#e9b509}{0 < x < 1{,}6}\) infrage.
In diesem Bereich verläuft der Graph von \(f\) oberhalb der \(x\)-Achse und die momentane Änderungsrate der Staulänge ist somit positiv. Die Staulänge nimmt also im Bereich \(\textcolor{#e9b509}{0 < x < 1{,}6}\) zu.
Mit \(f'(x) = (5x^2-16x+8) \cdot \left( 1 - \dfrac{x}{4} \right)\) folgt (vgl. Angabe Aufgabe 1):
\[\begin{align*}f'(x) &= 0 \\[0.8em] (5x^2-16x+8) \cdot \left( 1 - \frac{x}{4} \right) &= 0 &&| \;(0 < x < 1{,}6)\\[0.8em] \Rightarrow \; 5x^2-16x+8 = 0 \; \vee \; x &= 4 &&| \; x = 4 \textcolor{#cc071e}{\notin} 0 < x < 1{,}6 \\[0.8em] \end{align*}\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) anwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}x_{1,2} &= \frac{16 \pm \sqrt{(-16)^2 - 4 \cdot 5 \cdot 8}}{2 \cdot 5} = \frac{16 \pm \sqrt{96}}{10} \end{align*}\]
\[x_1 = \frac{16 + \sqrt{96}}{10} \approx 2{,}58\]
\[x_2 = \frac{16 - \sqrt{96}}{10} \approx 0{,}62\]
Die im Sachzusammenhang sinnvolle Lösung ist \(x = 0{,}62\).
\(0{,}62 \cdot 60\;\text{min} \approx 37\;\text{min}\) (optional)
Um 06:37 Uhr nimmt die Staulänge am stärksten zu.
oder
0,62 h nach 06:00 Uhr nimmt die Staulänge am stärksten zu.
