Berechnen Sie \(f(-5)\) und \(f(-1{,}5)\) und skizzieren Sie \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1.

(4 BE)

Lösung zu Teilaufgabe 1d

Skizzieren eines Funktionsgraphen

Funktionswerte \(f(-5)\) und \(f(-1{,}5)\)

\[f(x) = \frac{1}{x + 1} - \frac{1}{x + 3}\]

\[f(-5) = \frac{1}{-5 + 1} - \frac{1}{-5 + 3} = -\frac{1}{4} - \left( -\frac{1}{2} \right) = \frac{1}{4}\]

\[f(-1{,}5) = \frac{1}{-1{,}5 + 1} - \frac{1}{-1{,}5 + 3} = -\frac{1}{\frac{1}{2}} - \frac{1}{\frac{3}{2}} = -2 - \frac{2}{3} = -2\frac{2}{3}\]

Skizzieren von \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse

Bisherige Ergebnisse aus den Teilaufgabe 1b und 1c:

Die \(x\)-Achse ist horizontale Asymptote von \(G_{f}\).

Die Geraden mit den Gleichungen \(x = -3\) und \(x = -1\) sind senkrechte Asymptoten von \(G_{f}\). \(G_{f}\) besitzt für \(x = -3\) und \(x = -1\) jeweils eine Polstelle mit Vorzeichenwechsel.

Schnittpunkt von \(G_{f}\) mit der \(y\)-Achse: \(S_{y} \left(0|\frac{2}{3}\right)\)

Hochpunkt von \(G_{f}\): \(HoP\,(-2|-2)\)

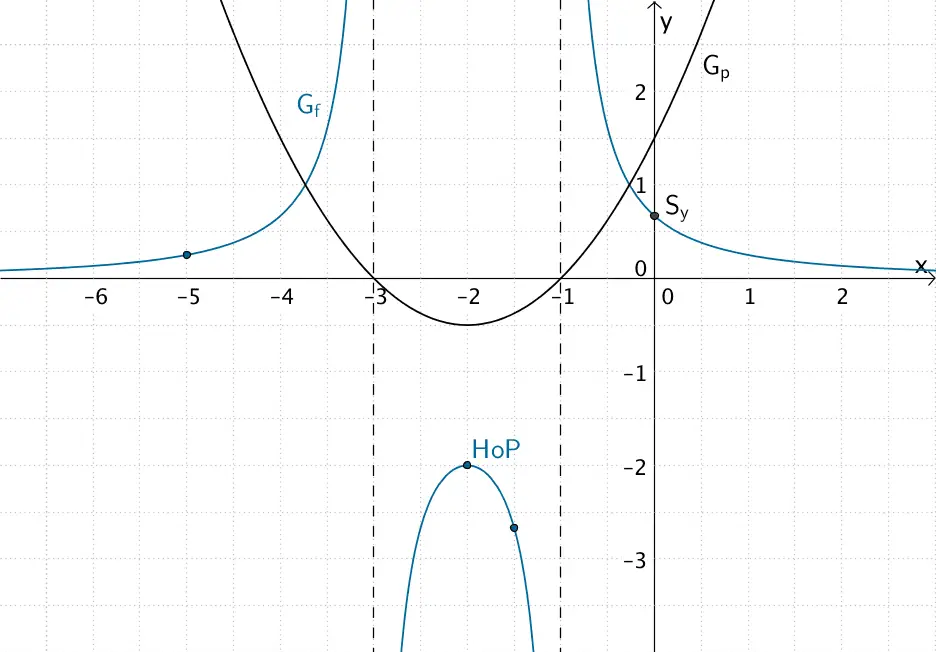
Verlauf des Graphen der Funktion \(f\)