Zeichnen Sie die Parabel \(G_h\) - unter Berücksichtigung des Scheitels - im Bereich \(-2 \leq x \leq 4\) in Ihre Zeichnung aus Aufgabe 1d ein. Spiegelt man diesen Teil von \(G_h\) an der Winkelhalbierenden \(w\), so entsteht eine herzförmige Figur; ergänzen Sie Ihre Zeichnung dementsprechend.
(4 BE)
Lösung zu Teilaufgabe 2b
Zeichnung der Parabel \(G_{h}\) unter Berücksichtigung des Scheitels für \(-2 \leq x \leq 4\)
Ermitteln der Scheitelpunktkoordinaten
Anmerkung: Der Teil der Parabel \(G_{h}\) und deren Scheitelpunkt lässt sich anhand einer mittels Taschenrechner erstellten Wertetabelle zeichnen. Die Aufgabenstellung schreibt lediglich die Berücksichtigung des Scheitels vor, nicht aber die Methode, den Scheitelpunkt zu bestimmen. In jedem Fall sollte die Zeichnung den Scheitelpunkt enthalten und den Verlauf von \(G_h\) in der Umgebung des Scheitels möglichst genau beschreiben. Die nachfolgenden drei Lösungsansätze zeigen Alternativen zur Bestimmung der Scheitelpunktkoordinaten auf.
1. Lösungsansatz: Interpretation der Eigenschaft von \(G_f\) aus Teilaufgabe 1b
Aus Teilaufgabe 1b ist bekannt, dass die Steigung der Tangente an \(G_f\) im Punkt \((6|2)\) gegen Unendlich geht. Da man den Graphen von \(f^{-1}\) durch Spiegelung an der Winkelhalbierenden des I. und III. Quadranten erhält, lässt sich schlussfolgern, dass die Steigung der Tangente an \(G_{f^{-1}}\) im Punkt \((2|6)\) gegen Null geht. Wie in Aufgabe 2 eingangs beschrieben, ist der Graph der Umkehrfunktion \(f^{-1}\) ein Teil der Parabel \(G_h\). Folglich weißt die waagrechte Tangente im Punkt \((2|6)\) auf den Scheitelpunkt der Parabel \(G_{h}\) hin.
\(\Longrightarrow \quad\) Scheitelpunkt der Parabel \(G_{h}\): \(S\,(2|6)\)
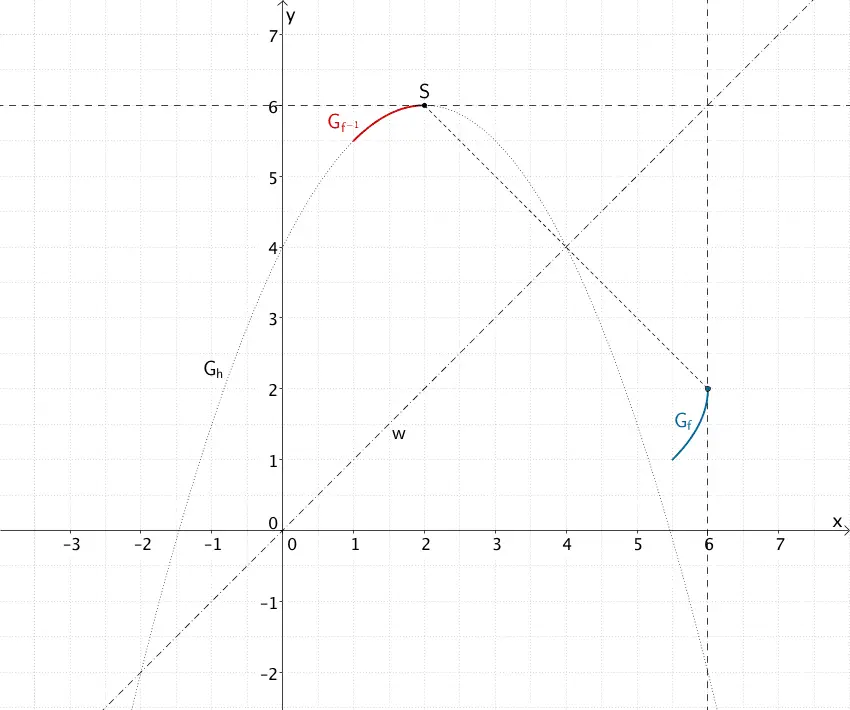
Verhalten von \(G_{f}\) im Punkt \((6|2)\), Verhalten von \(G_{f^{-1}}\) im Punkt \((2|6)\), Scheitelpunkt \(S\) der Parabel \(G_h\)
2. Lösungsansatz: Quadratische Ergänzung
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\,; \quad D = \mathbb R\]
Mit Hilfe der Quadratischen Ergänzung wird der Funktionsterm der Funktion \(h\) in die Scheitelpunktform umformuliert. Aus der Scheitelpunktform lässt sich der Scheitelpunkt der Parabel \(G_{h}\) ablesen.
Quadratische Funktion:
\[f(x) = ax^2 + bx + c\,; \quad a, b, c \, \in \, \mathbb R\,, a \neq 0\]
Scheitelpunktform
\[f(x) = a(x - d)^2 + e\]
Scheitelpunkt
\[S\,(d|e) \qquad d = -\frac{b}{2a}\,; \quad e = c - \frac{b^2}{4a}\]
\[\begin{align*}h(x) &= -\frac{1}{2}x^2 + 2x + 4 & &| \; \text{Faktor} \; -\frac{1}{2} \; \text{ausklammern} \\[0.8em] &= -\frac{1}{2} \cdot \left( x^2 - 4x - 8 \right) & &| \; \text{Quadratische Ergänzung} \\[0.8em] &= -\frac{1}{2} \cdot \Big( \underbrace{x^2 - 4x + 2^2}_{a^2 \, - \, 2ab \, + \, b^2 \, = \, (a \, - \, b)^2} -2^2 - 8 \Big) & &| \; \text{2. binomische Formel anwenden} \\[0.8em] &= -\frac{1}{2} \cdot \left[ (x - 2)^2 - 12 \right] & &| \; \text{Faktor} \; -\frac{1}{2} \; \text{ausmultiplizieren} \\[0.8em] &= -\frac{1}{2} \cdot (x - 2)^2 + 6 \end{align*}\]
\(\Longrightarrow \quad\) Scheitelpunkt der Parabel \(G_{h}\): \(S\,(2|6)\)
3. Lösungsansatz: Extrempunkt von \(h\) bestimmen
Der Scheitelpunkt ist der einzige Extrempunkt einer Parabel. Die Art des Extrempunkts muss in diesem Fall nicht nachgewiesen werden. Es interessieren lediglich die Scheitelpunktkoordinaten für die zu erstellende Zeichnung von \(G_h\)
\[h(x) = - \frac{1}{2}x^2 + 2x +4\,; \quad D = \mathbb R\]
Notwendige Bedingung für die Extremstelle von \(h\):
\[h'(x) \overset{!}{=} 0\]
Erste Ableitung \(h'\) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[h'(x) = -\frac{1}{2} \cdot 2 \cdot x + 2 + 0 = -x + 2\]
\[\begin{align*}h'(x) &= 0 \\[0.8em] - x + 2 &= 0 & &| + x \\[0.8em] 2 &= x \end{align*} \]
\[h(2) = -\frac{1}{2} \cdot 2^2 + 2 \cdot 2 + 4 = 6\]
\(\Longrightarrow \quad\) Scheitelpunkt der Parabel \(G_{h}\): \(S\,(2|6)\)
Zeichnung der Parabel \(G_h\) für \(-2 \leq x \leq 4\) erstellen
Schnittpunkte mit der Winkelhalbierenden: \(S_{1}\,(-2|-2)\,, \enspace S_{2}\,(4|4)\;\) (siehe Teilaufgabe 2a)
Scheitelpunkt \(S\,(2|6)\)
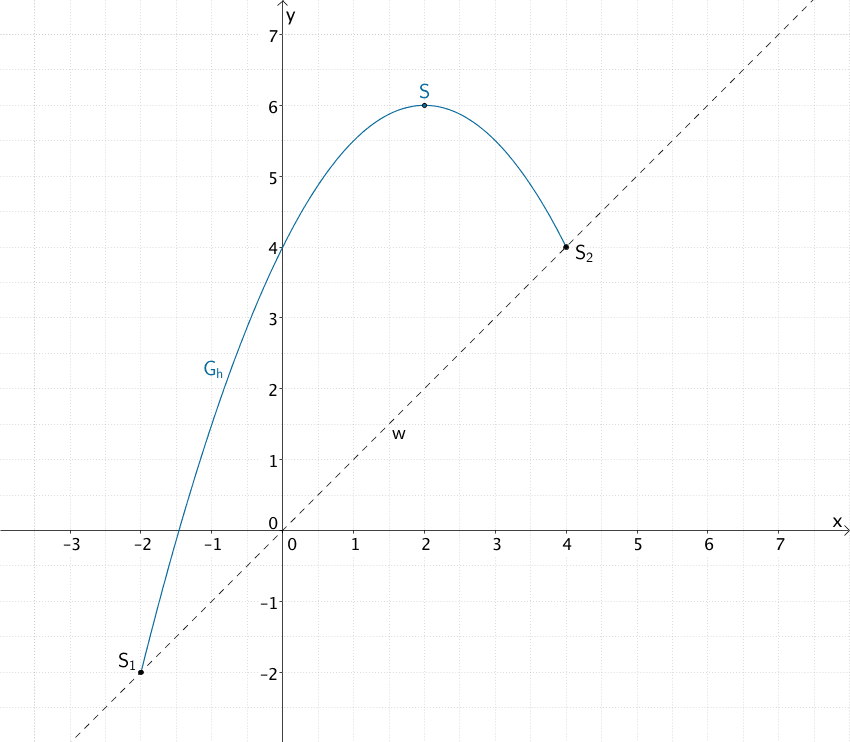
Graph der Funktion \(h\) für \(-2 \leq x \leq 4\)
Spiegeln des Teils der Parabel \(G_{h}\) an der Winkelhalbierenden \(w\)
Die Zeichnung wird genauer, wenn neben dem Scheitelpunkt \(S\) noch weitere Punkte von \(G_{h}\) an der Winkelhalbierenden \(w\) gespiegelt werden.
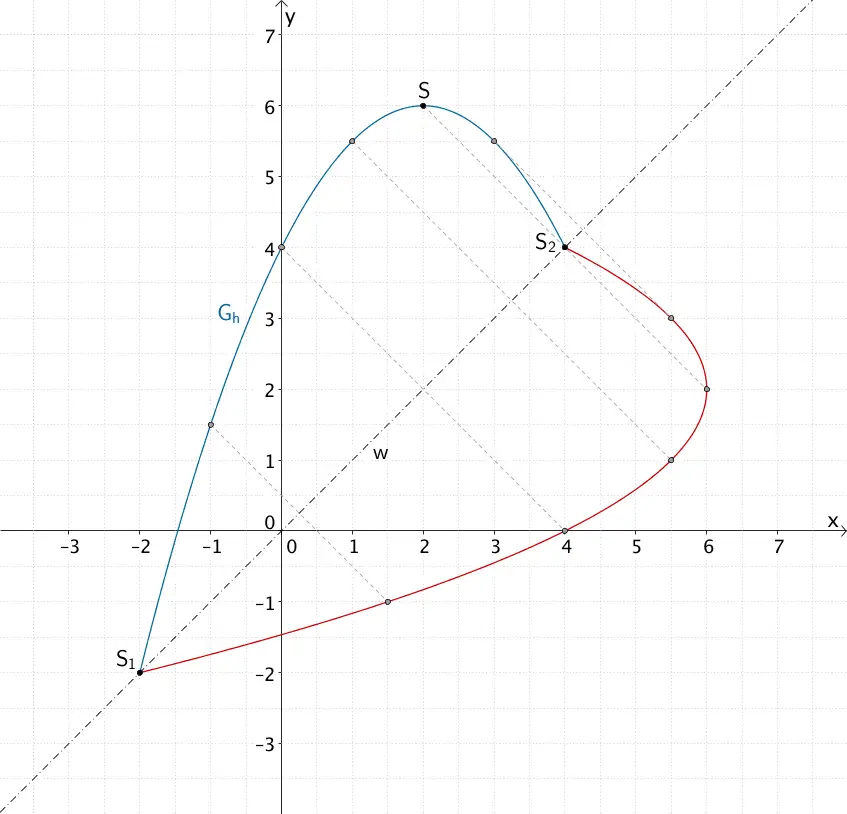
Parabel \(G_h\) für \(-2 \leq x \leq 4\) und deren an der Winkelhalbierenden \(w\) gespiegeltes Bild


