Abiturlösungen Mathematik Bayern 2011 G8 Analysis I
Gegeben ist die Funktion \(\displaystyle f : x \mapsto \frac{2x + 3}{4x + 5}\) mit maximaler Definitionsmenge \(D\). Geben Sie \(D\) an und ermitteln Sie einen möglichst einfachen Funktionsterm für die Ableitung \(f'\) von \(f\).
(4 BE)
- Details
- Hauptkategorie: Analysis I
Zeigen Sie, dass \(F : x \mapsto \frac{1}{4}x^2 \cdot (2\ln x - 1)\) mit Definitionsmenge \(\mathbb R^+\) eine Stammfunktion der in \(\mathbb R^+\) definierten Funktion \(f : x \mapsto x \cdot \ln x\) ist. Bestimmen Sie den Term derjenigen Stammfunktion von \(f\), die in \(x = 1\) eine Nullstelle hat.
(5 BE)
- Details
- Hauptkategorie: Analysis I
Die Anzahl der auf der Erde lebenden Menschen wuchs von 6,1 Milliarden zu Beginn des Jahres 2000 auf 6,9 Milliarden zu Beginn des Jahres 2010.Dieses Wachstum lässt sich näherungsweise durch eine Exponentialfunktion mit einem Term der Form \(N(x) = N_0 \cdot e^{k \cdot (x - 2000)}\) beschreiben, wobei \(N(x)\) die Anzahl der Menschen zu Beginn des Jahres \(x\) ist.
Bestimmen Sie \(N_0\) und \(k\).
(5 BE)
- Details
- Hauptkategorie: Analysis I
Betrachtet wird die Aussage \(\displaystyle \int_{0}^{\pi} \sin(2x)\,dx = 0\).
Machen Sie ohne Rechnung anhand einer sorgfältigen Skizze plausibel, dass die Aussage wahr ist.
(3 BE)
- Details
- Hauptkategorie: Analysis I
Weisen Sie mithilfe einer Stammfunktion die Gültigkeit der Aussage durch Rechnung nach.
(3 BE)
- Details
- Hauptkategorie: Analysis I
Gegeben ist die Funktion \(f \colon x \mapsto \sqrt{x + 3}\) mit Definitionsmenge \(D_f\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\), einen beliebigen Punkt \(Q(x|f(x))\) auf \(G_f\) sowie den Punkt \(P(1{,}5|0)\) auf der \(x\)-Achse.
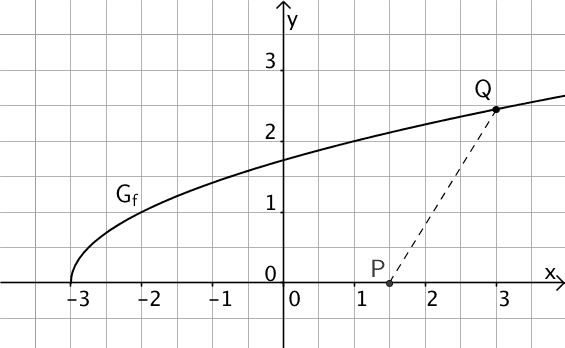Abb. 1
Begründen Sie, dass \(D_f = [-3;+\infty[\) die maximale Definitionsmenge von \(f\) ist. Wie geht \(G_f\) aus dem Graphen der in \(\mathbb R_0^+\) definierten Funktion \(w : x \mapsto \sqrt{x\;}\;\) hervor?
(2 BE)
- Details
- Hauptkategorie: Analysis I
Zeigen Sie, dass für die Entfernung \(d(x)\) des Punktes \(Q(x|f(x))\) vom Punkt \(P(1{,}5|0)\) gilt: \(d(x) = \sqrt{x^2 - 2x + 5{,}25}\).
(4 BE)
- Details
- Hauptkategorie: Analysis I
Bestimmen Sie rechnerisch die Koordinaten desjenigen Graphenpunkts \(Q_E(x_E|y_E)\), der von \(P\) den kleinsten Abstand hat. Tragen Sie \(Q_E\) in Abbildung 1 ein.
(zur Kontrolle: \(x_E = 1\))
(7 BE)
- Details
- Hauptkategorie: Analysis I
Weisen Sie nach, dass die Verbindungsstrecke \([PQ_E]\) und die Tangente an \(G_f\) im Punkt \(Q_E\) senkrecht zueinander sind.
(5 BE)
- Details
- Hauptkategorie: Analysis I
Berechnen Sie den Inhalt des Flächenstücks, das von \(G_f\), der \(x\)-Achse und der Strecke \([PQ_E]\) begrenzt wird.
(6 BE)
- Details
- Hauptkategorie: Analysis I
Abbildung 2 zeigt den Graphen \(G_g\) einer in \(\mathbb R \backslash \{1\}\) definierten gebrochen-rationalen Funktion \(g\) mit folgenden Eigenschaften:
-
Die Funktion \(g\) hat in \(x = 1\) eine Polstelle ohne Vorzeichenwechsel;
-
\(G_g\) verläuft stets oberhalb seiner schrägen Asymptote, die durch die Gleichung \(y = \frac{1}{2}x - 1\) gegeben ist;
-
die einzige Nullstelle von \(g\) ist \(x = -1\).
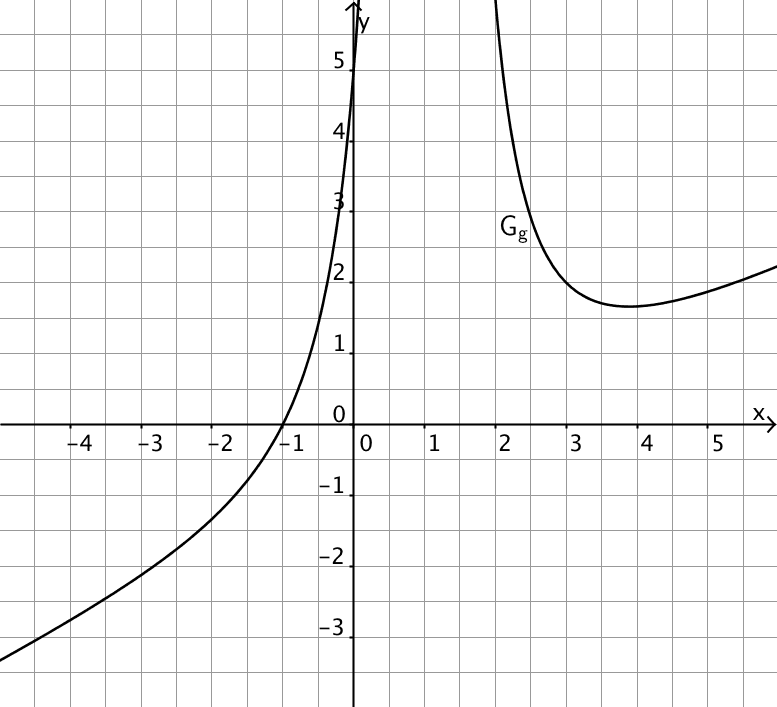Abb. 2
Ermitteln Sie mithilfe von Abbildung 2 näherungsweise den Wert der Ableitung \(g'\) von \(g\) an der Stelle \(x = -1\); veranschaulichen Sie Ihr Vorgehen durch geeignete Eintragungen in der Abbildung.
Aus der Gleichung der schrägen Asymptote ergibt sich unmittelbar das Verhalten der Ableitung \(g'\) für \(x \to +\infty\) und \(x \to -\infty\). Geben Sie dieses Verhalten an und skizzieren Sie den Graphen von \(g'\) in Abbildung 2.
(6 BE)
- Details
- Hauptkategorie: Analysis I
Die Funktion \(g\) hat eine Funktionsgleichung der Form I, II oder III mit \(a \in \mathbb R \backslash \{0\}\):
\[\textsf{I}\enspace y = x - 1 + \frac{a}{(x - 1)^2}\]
\[\textsf{II}\enspace y = \frac{1}{2}x - 1 + \frac{a}{x - 1}\]
\[\textsf{III}\enspace y = \frac{1}{2}x - 1 + \frac{a}{(x - 1)^2}\]
Begründen Sie, dass weder eine Gleichung der Form I noch eine der Form II als Funktionsgleichung von \(g\) infrage kommt.
Die Funktionsgleichung von \(g\) hat also die Form III. Bestimmen Sie den passenden Wert von \(a\).
(5 BE)
- Details
- Hauptkategorie: Analysis I
Betrachtet wird nun die Funktion \(h\) mit \(h(x) = \ln(g(x))\). Geben Sie mithilfe des Verlaufs von \(G_g\) die maximale Definitionsmenge \(D_h\) von \(h\), das Verhalten von \(h\) an den Grenzen von \(D_h\) sowie einen Näherungswert für die Nullstelle von \(h\) an.
(5 BE)
- Details
- Hauptkategorie: Analysis I
2023 Christian Rieger・mathelike
