Schwarze und weiße Kugeln sind wie folgt auf drei Urnen verteilt:

Aus Urne A wird zunächst eine Kugel zufällig entnommen und in Urne B gelegt. Anschließend wird aus Urne B eine Kugel zufällig entnommen und in Urne C gelegt. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich danach in Urne C zwei weiße Kugeln und eine schwarze Kugel befinden.
(2 BE)
Lösung zu Teilaufgabe 2a
Mehrstufiges Zufallsexperiment, Baumdiagramm, Pfadregeln
Veranschaulichung des Zufallsexperiments:
\(S\): schwarze Kugel, \(W\): weiße Kugel
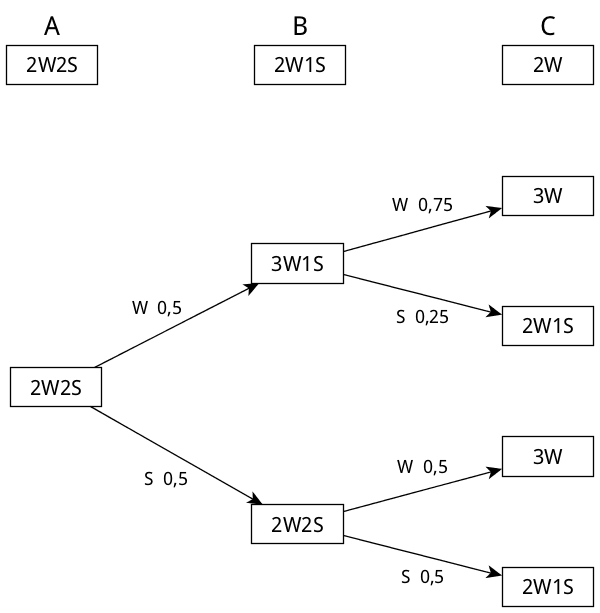
Ausgangszustand der Urnen A, B und C sowie Ablauf und Ergebnisse des Zufallsexperiments
Darstellung als Baumdiagramm:
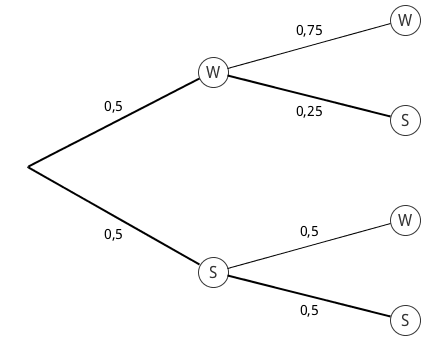
Baumdiagramm des Zufallsexperiments
In Urne C befinden sich zu Beginn zwei weiße Kugeln (vgl. Abbildung Angabe). Die Aufgabenstellung fragt nach der Wahrscheinlichkeit für das Ereignis „In Urne C befinden sich zwei weiße und eine schwarze Kugel."
Im Sinne der Aufgabenstellung sind also diejenigen Pfade relevant, die in der zweiten Stufe die Entnahme einer schwarzen Kugel aus Urne B darstellen.
Wahrscheinlichkeit des Ereignisses „In Urne C befinden sich zwei weiße und eine schwarze Kugel."berechnen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(\text{„2W1S"}) &= P(\{W,S\}) + P(\{S,S\}) \\[0.8em] &= \underbrace{\underbrace{0{,}5 \cdot 0{,}25}_{\large{\text{1. Pfadregel}}} + \underbrace{0{,}5 \cdot 0{,}5}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= 0{,}375 \end{align*}\]


