Ermitteln Sie die Wahrscheinlichkeit dafür, dass an die ersten drei Personen drei unterschiedliche Beträge ausbezahlt werden, die in der Summe 12 € ergeben.
(3 BE)
Lösung zu Teilaufgabe 2d
\[\begin{align*}&\quad \; P(\text{„Drei untersch. Auszahlungen, in Summe 12 €"}) = \\[0.8em] &= P(Z = 1) \cdot P(Z = 2) \cdot P(Z = 3) \cdot 3! \\[0.8em] &= \frac{1}{3} \cdot \frac{1}{4} \cdot \frac{1}{12} \cdot 6 = \frac{6}{144} = \frac{1}{24}\end{align*}\]
Ausführliche Erklärung (nicht verlangt)
„Für jede Ziffer 2, die auf den erzielten Sektoren steht, werden 2 € ausbezahlt. Die Zufallsgröße \(\boldsymbol{Z}\) beschreibt, wie oft die Ziffer 2 auf den erzielten Sektoren insgesamt vorkommt." (vgl. Angabe Aufgabe 2)
| \(k\) | \(0\) | \(\textcolor{#e9b509}{1}\) | \(\textcolor{#e9b509}{2}\) | \(\textcolor{#e9b509}{3}\) |
| Auszahlung in € | \(0\) | \(\textcolor{#cc071e}{2}\) | \(\textcolor{#cc071e}{4}\) | \(\textcolor{#cc071e}{6}\) |
| \(P(Z = k)\) | \(\dfrac{1}{3}\) | \(\textcolor{#89ba17}{\dfrac{1}{3}}\) | \(\textcolor{#89ba17}{\dfrac{1}{4}}\) | \(\textcolor{#89ba17}{\dfrac{1}{12}}\) |
Drei unterschiedliche Auszahlungen, die in der Summe 12 € ergeben, können nur aus den Auszahlungsbeträgen 2 €, 4 € und 6 € bestehen.
Es gibt drei Möglichkeiten einen der drei verschiedenen Beträge an die erste Person auszuzahlen. Es verbleiben zwei mögliche Beträge für die Auszahlung an die zweite Person und schließlich noch ein möglicher Auszahlungsbetrag für die dritte Person.
Allgemeines Zählprinzip
Wird ein Zufallsexperiment in \(k\) Stufen durchgeführt und gibt es in der ersten Stufe \(n_{1}\), in der zweiten Stufe \(n_{2}\) und in der \(k\)-ten Stufe \(n_{k}\) mögliche Ergebnisse, so gilt für die Anzahl \(N\) der insgesamt möglichen Ergebnisse:
\[N = n_{1} \cdot n_{2} \cdot \dots \cdot n_{k}\]
Nach dem allgemeinen Zählprinzip gibt es dann \(\textcolor{#0087c1}{3} \cdot \textcolor{#0087c1}{2} \cdot \textcolor{#0087c1}{1} = \textcolor{#0087c1}{3!}\) Möglichkeiten, in welcher Reihenfolge die unterschiedlichen Beträge an die ersten drei Personen ausbezahlt werden können (Entspricht dem Urnenmodell „Ziehen ohne Zurücklegen und mit Beachtung der Reihenfolge").
Grundformeln der Kombinatorik
Viele mehrstufige Zufallsexperimente können mithilfe sogenannter Urnenmodelle veranschaulicht werden. Aus einer Urne mit \(\boldsymbol{n}\) unterscheidbaren Kugeln wird \(\boldsymbol{k}\)-mal eine Kugel gezogen.
Die Modelle lassen sich in die Fälle mit/ohne Zurücklegen bzw. mit/ohne Beachtung der Reihenfolge der gezogenen Kugeln unterteilen.


\[n^{k}\]
\(n\): Anzahl der Unterscheidungsmerkmale
\(k\): Anzahl der Wiederholungen
Beispiel
Wieviele Möglichkeiten gibt es, vier Wände eines Kinderzimmers in den Farben Seesternorange, Frochschgrün, Libellenblau, Käferrot oder Bienengelb zu streichen?
\(\textcolor{#cc071e}{n = 5}\), da fünf verschiedene Farben zur Verfügung stehen.
\(\textcolor{#0087c1}{k = 4}\), da viermal eine Farbe zu wählen ist.
Somit \(\textcolor{#cc071e}{5}^{\textcolor{#0087c1}{4}} = 625\) Möglichkeiten
- nicht abiturrelevant -

\(n \cdot (n - 1) \cdot ... \cdot (n - k + 1) = \dfrac{n!}{(n-k)!}\)
Spezialfall: \(n!\) für \(k = n\) (Permutationen)
\(n\): Anzahl der Unterscheidungsmerkmale
\(k\): Anzahl der Wiederholungen
Beispiel
Wieviele Möglichkeiten gibt es, vier Wände eines Kinderzimmers in den Farben Seesternorange, Frochschgrün, Libellenblau, Käferrot oder Bienengelb zu streichen, wenn jede Wand eine andere Farbe bekommen soll?
\(\textcolor{#cc071e}{n = 5}\), da fünf verschiedene Farben zur Verfügung stehen.
\(\textcolor{#0087c1}{k = 4}\), da viermal eine Farbe zu wählen ist.
Für die erste Wand stehen fünf Farben zur Auswahl, für die zweite Wand noch vier Farben, für die dritte Wand noch drei Farben und für die vierte Wand schließlich nur noch zwei Farben.
Somit \(\underbrace{\textcolor{#cc071e}{5} \cdot 4 \cdot 3 \cdot 2}_{\textcolor{#0087c1}{k\,=\,4}} = 120\) Möglichkeiten
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
Der Binomialkoeffizient \(\displaystyle \binom{n}{k}\) gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
Beispiel
Von 30 Schüler*innen können acht Schüler*innen an einer Studienfahrt teilnehmen. Die Teilnehmer*innen werden per Los entschieden. Wieviele mögliche Gruppierungen gibt es?
\(n = 30\)
\(k = 8\)
Somit \(\displaystyle \binom{30}{8} = 5852925\) mögliche Gruppen aus jeweils acht Schüler*innen.
Veranschaulichung mithilfe eines Baumdiagramms:
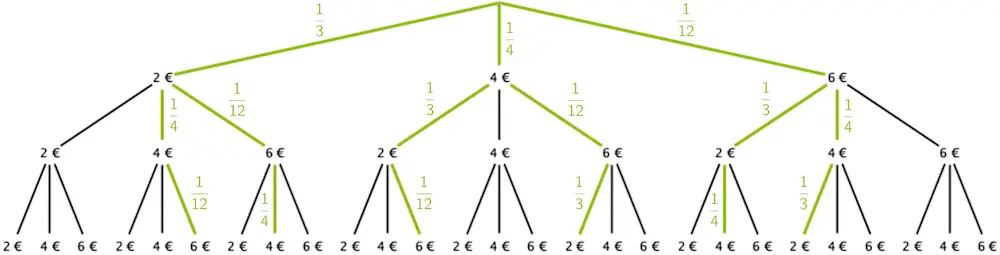
Jedes der \(\textcolor{#0087c1}{3!} = \textcolor{#0087c1}{6}\) Ergebnisse des Ereignisses „An die ersten drei Personen werden drei unterschiedliche Beträge ausbezahlt, die in der Summe 12 € ergeben." tritt gemäß der 1. Pfadregel mit der Wahrscheinlichkeit \(\textcolor{#89ba17}{\dfrac{1}{3}} \cdot \textcolor{#89ba17}{\dfrac{1}{4}} \cdot \textcolor{#89ba17}{\dfrac{1}{12}}\) ein.
Somit ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}&\quad \; P(\text{„Drei untersch. Auszahlungen, in Summe 12 €"}) = \\[0.8em] &= P(\textcolor{#e9b509}{Z = 1}) \cdot P(\textcolor{#e9b509}{Z = 2}) \cdot P(\textcolor{#e9b509}{Z = 3}) \cdot \textcolor{#0087c1}{3!} \\[0.8em] &= \underbrace{\textcolor{#89ba17}{\frac{1}{3}} \cdot \textcolor{#89ba17}{\frac{1}{4}} \cdot \textcolor{#89ba17}{\frac{1}{12}}}_{\text{1. Pfadregel}} \cdot \textcolor{#0087c1}{6} \\[0.8em] &= \frac{6}{144} = \frac{1}{24}\end{align*}\]


