Berechnen Sie den Inhalt der Fläche, die von \(G_{f}\) und der Strecke \([AB]\) eingeschlossen wird.
(5 BE)
Lösung zu Teilaufgabe 1d
\[f(x) = \frac{6x}{x^{2} - 4}; \; D_{f} = \mathbb R \backslash \{-2;2\}\]
![Flächeninhalt A des Flächenstücks, welches der Graph von f und die Strecke [AB] einschließen](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_1d1.png)
Flächeninhalt \(\textcolor{#0087c1}{A}\) der Fläche, welche \(G_{f}\) und die Strecke \([AB]\) einschließen.
1. Möglichkeit: Flächeninhalt eines Trapezes berücksichtigen
![Flächeninhalt des Flächenstücks, welches der Graph der Funktion f im Intervall [3;8] mit der x-Achse einschließt und Trapez, das die Strecke [AB] mit der x-Achse bildet](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_1d2.png)
\[\textcolor{#0087c1}{A} = \textcolor{#cc071e}{A_{\text{Trapez}}} - \int_{3}^{8}f(x)dx\]
Flächeninhalt des Trapezes berechnen:
Flächeninhalt eines Trapezes
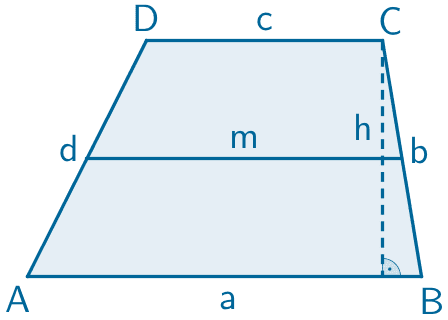
\[A = m \cdot h = \frac{a + c}{2} \cdot h\]
\[\begin{align*} \textcolor{#cc071e}{A_{\text{Trapez}}} &= \frac{\textcolor{#cc071e}{y_{A}} + \textcolor{#cc071e}{y_{B}}}{2} \cdot (\textcolor{#cc071e}{x_{B}} - \textcolor{#cc071e}{x_{A}}) \\[0.8em] &= \frac{\textcolor{#cc071e}{3{,}6} + \textcolor{#cc071e}{0{,}8}}{2} \cdot (\textcolor{#cc071e}{8} - \textcolor{#cc071e}{3}) \\[0.8em] &= 2{,}2 \cdot 5 \\[0.8em] &= \textcolor{#cc071e}{11} \end{align*}\]
Wert des bestimmten Integrals \(\displaystyle \int_{3}^{8}f(x)dx\) berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*} \int_{3}^{8}f(x)dx &= \int_{3}^{8} \frac{6x}{x^{2} - 4}dx \\[0.8em] &= \int_{3}^{8} \frac{3 \cdot \textcolor{#e9b509}{2x}}{\textcolor{#e9b509}{x^{2} - 4}}dx \\[0.8em] &= 3 \cdot \int_{3}^{8}\frac{\textcolor{#e9b509}{2x}}{\textcolor{#e9b509}{x^{2} - 4}} dx &&| \; \int \frac{\textcolor{#e9b509}{f'(x)}}{\textcolor{#e9b509}{f(x)}} = \textcolor{#e9b509}{\ln\vert f(x) \vert + C} \; \text{(vgl. Merkhilfe)} \\[0.8em] &= 3 \cdot \big[\textcolor{#e9b509}{\underbrace{\ln{\vert x^{2} - 4 \vert}}_{\text{Stammfunktion}}}\big]_{\textcolor{#89ba17}{3}}^{\textcolor{#89ba17}{8}} \\[0.8em] &= 3 \cdot \left( \ln{\vert \textcolor{#89ba17}{8}^{2} - 4 \vert} - \ln{\vert \textcolor{#89ba17}{3}^{2} - 4\vert} \right) \\[0.8em] &= 3 \cdot \left( \ln{\textcolor{#e9b509}{60}} - \ln{\textcolor{#e9b509}{5}} \right) &&| \; \log_{a}{\frac{\textcolor{#e9b509}{b}}{\textcolor{#e9b509}{c}}} = \log_{a}{\textcolor{#e9b509}{b}} - \log_{a}{\textcolor{#e9b509}{c}} \; \text{(vgl. Merkhilfe)}\\[0.8em] &= 3 \cdot \ln{\frac{\textcolor{#e9b509}{60}}{\textcolor{#e9b509}{5}}} \\[0.8em] &= 3\ln{12} \end{align*}\]
Flächeninhalt \(\textcolor{#0087c1}{A}\) berechnen:
\[\begin{align*}\textcolor{#0087c1}{A} &= \textcolor{#cc071e}{A_{\text{Trapez}}} - \int_{3}^{8}f(x)dx \\[0.8em] &= \textcolor{#cc071e}{11} - 3\ln{12}\end{align*}\]
2. Möglichkeit: Differenzfunktion integrieren
![Gerade AB, Flächeninhalt A des Flächenstücks, welches der Graph von f und die Strecke [AB] einschließen](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_1d3.png)
Es sei \(\textcolor{#cc071e}{g}\) die Gerade, welche durch die Punkte \(\textcolor{#cc071e}{A(3|3{,}6)}\) und \(\textcolor{#cc071e}{B(8|0{,}8)}\) verläuft.
Der Flächeninhalt \(\textcolor{#0087c1}{A}\) lässt sich durch Integration der Differenzfunktion \(\textcolor{#cc071e}{g(x)} - f(x)\) berechnen.
\[\textcolor{#0087c1}{A} = \int_{3}^{8}[\textcolor{#cc071e}{g(x)} - f(x)]dx\]
Funktionsterm \(\textcolor{#cc071e}{g(x)}\) der Gerade \(\textcolor{#cc071e}{g}\) bestimmen:
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[\textcolor{#cc071e}{g(x)} = \boldsymbol{m}x + \boldsymbol{t}\]
Zunächst wird die Steigung \(\bf{m}\) mithilfe der Koordinaten der Punkte \(\textcolor{#cc071e}{A(3|3{,}6)}\) und \(\textcolor{#cc071e}{B(8|0{,}8)}\) berechnet.
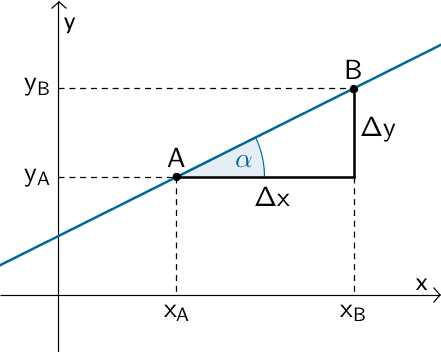
Steigung \(m\) einer Gerade
\[m = \frac{\Delta y}{\Delta x} = \frac{y_B - y_A}{x_B - x_A}\]
\[m = \tan \alpha \quad (\alpha \neq 90^{\circ})\]
\[m = \frac{\textcolor{#cc071e}{y_{B}} - \textcolor{#cc071e}{y_{A}}}{\textcolor{#cc071e}{x_{B}} - \textcolor{#cc071e}{x_{A}}} = \frac{\textcolor{#cc071e}{0{,}8} - \textcolor{#cc071e}{3{,}6}}{\textcolor{#cc071e}{8} - \textcolor{#cc071e}{3}} = \frac{-2{,}8}{5} = -0{,}56\]
\[\Rightarrow \enspace g(x) = -0{,}56x + t\]
Durch Einsetzen der Koordinaten von \(\textcolor{#cc071e}{A(3|3{,}6)}\) oder \(\textcolor{#cc071e}{B(8|0{,}8)}\) kann der y-Achsenabschnitt \(\bf{t}\) ermittelt werden.
\[\begin{align*}\textcolor{#cc071e}{A(3|3{,}6)} \in \textcolor{#cc071e}{g} \colon \; \textcolor{#cc071e}{3{,}6} &= -0{,}56 \cdot \textcolor{#cc071e}{3} + t \\[0.8em] 3{,}6 &= -1{,}68 + t &&| + 1{,}68 \\[0.8em] 5{,}28 &= t\end{align*}\]
oder
\[\begin{align*}\textcolor{#cc071e}{B(8|0{,}8)} \in \textcolor{#cc071e}{g} \colon \; \textcolor{#cc071e}{0{,}8} &= -0{,}56 \cdot \textcolor{#cc071e}{8} + t \\[0.8em] 3{,}6 &= -4{,}48 + t &&| + 4{,}48 \\[0.8em] 5{,}28 &= t\end{align*}\]
\[\Rightarrow \enspace \textcolor{#cc071e}{g(x)} = \textcolor{#cc071e}{-0{,}56x + 5{,}28}\]
Flächeninhalt \(\textcolor{#0087c1}{A}\) berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*}\textcolor{#0087c1}{A} &= \int_{3}^{8}[\textcolor{#cc071e}{g(x)} - f(x)]dx \\[0.8em] &= \int_{3}^{8}\left( \textcolor{#cc071e}{-0{,}56 + 5{,}28} - \frac{6x}{x^{2} - 4} \right)dx \\[0.8em] &= \int_{3}^{8}\left( \textcolor{#cc071e}{-0{,}56 + 5{,}28} - 3 \cdot \frac{\textcolor{#e9b509}{2x}}{\textcolor{#e9b509}{x^{2} - 4}} \right)dx &&| \; \int \textcolor{#cc071e}{x^{r}} dx = \textcolor{#cc071e}{\frac{x^{r + 1}}{r + 1} + C} \;(r \neq -1) \\ &&&| \int \frac{\textcolor{#e9b509}{f'(x)}}{\textcolor{#e9b509}{f(x)}}dx = \textcolor{#e9b509}{\ln{\vert f(x) \vert} + C} \; \text{(vgl. Merkhilfe)} \\[0.8em] &= \Big[ \underbrace{\textcolor{#cc071e}{-0{,}28x^{2} + 5{,}28x} + 3 \cdot \textcolor{#e9b509}{\ln{\vert x^{2} - 4 \vert}}}_{\large{\text{Stammfunktion von}\; \textcolor{#cc071e}{g(x)} \,-\, f(x)}} \Big]_{\textcolor{#89ba17}{3}}^{\textcolor{#89ba17}{8}} \\[0.8em] &= -0{,}28 \cdot \textcolor{#89ba17}{8}^{2} + 5{,}28 \cdot \textcolor{#89ba17}{8} - 3 \cdot \ln{\vert \textcolor{#89ba17}{8}^{2} - 4 \vert} \\[0.8em] & \quad \,-(-0{,}28 \cdot \textcolor{#89ba17}{3}^{2} + 5{,}28 \cdot \textcolor{#89ba17}{3} - 3 \cdot \ln{\vert \textcolor{#89ba17}{3}^{2} - 4 \vert}) \\[0.8em] &= 24{,}32 - 3\ln{60} - 13{,}32 + 3\ln{5} \\[0.8em] &= 11 - 3(\ln{\textcolor{#e9b509}{60}} - \ln{\textcolor{#e9b509}{5}}) &&| \; \log_{a}{\frac{\textcolor{#e9b509}{b}}{\textcolor{#e9b509}{c}}} = \log_{a}{\textcolor{#e9b509}{b}} - \log_{a}{\textcolor{#e9b509}{c}}\;\text{(vgl. Merkhilfe)} \\[0.8em] &= 11 - 3\ln{\frac{\textcolor{#e9b509}{60}}{\textcolor{#e9b509}{5}}} \\[0.8em] &= 11 - 3\ln{12}\end{align*}\]


