Berechnen Sie das Volumen \(V\) der Pyramide \(ABCDS\).
(zur Kontrolle: \(V = 72\))
(2 BE)
Lösung zu Teilaufgabe c
1. Möglichkeit: \(V = \frac{1}{3} \cdot G \cdot h\) (vgl. Merkhilfe)
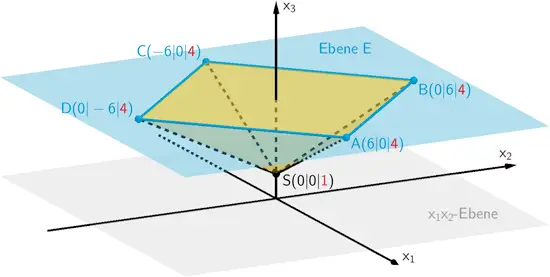
Die Höhe einer Pyramide ist definiert als der Abstand der Pyramidenspitze von der Ebene, in der die Grundfläche der Pyramide liegt.
Die Grundfläche \(ABCD\) liegt in der Ebene \(E\), welche im Abstand 4 parallel zur \(x_{1}x_{2}\)-Ebene ist (vgl. Teilaufgabe a). Die Spitze \(S(0|0|\textcolor{#cc071e}{1})\) hat von der \(x_{1}x_{2}\)-Ebene den Abstand 1.
Somit gilt für die Höhe \(h\) der Pyramide \(ABCDS\):
\[h = \textcolor{#cc071e}{4} - \textcolor{#cc071e}{1} = 3\]
Flächeninhalt der quadratischen Grundfläche \(ABCD\) berechnen:
\(A(6|0|4)\), \(B(0|6|4)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{AB} &= \vert \overrightarrow{AB} \vert = \vert \overrightarrow{B} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 6 \\ 4 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} \right| = \left| \begin{pmatrix} -6 \\ 6 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-6)^{2} + 6^{2} + 0^{2}} = \sqrt{72}\end{align*}\]
\[A_{ABCD} = \overline{AB}^{2} = \sqrt{72}^{2} = 72\]
Volumen der Pyramide \(ABCDS\) berechne:
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\[V = \frac{1}{3} \cdot A_{ABCD} \cdot h = \frac{1}{\cancel{3}} \cdot 72 \cdot \cancel{3} = 72\]
2. Möglichkeit: Spatprodukt anwenden
Dieser rein vektorielle Lösungsansatz ist rechnerisch aufwendiger.
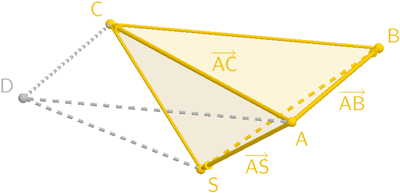
Beispielsweise spannen die drei linear unabhängigen Verbindungsvektoren \(\textcolor{#e9b509}{\overrightarrow{AB}}\), \(\textcolor{#e9b509}{\overrightarrow{AC}}\) und \(\textcolor{#e9b509}{\overrightarrow{AS}}\) einen Spat auf. Das Volumen der dreiseitigen Pyramide \(\textcolor{#e9b509}{ABCS}\) (vgl. Merkhilfe) nimmt ein Sechstel des Volumens des Spats ein. Das Volumen der Pyramide \(ABCDS\) ist doppelt so groß wie das Volumen der Pyramide \(ABCS\).
(vgl. Abiturskript - 2.1.5 Spatprodukt)
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
Verbindungsvektoren \(\textcolor{#e9b509}{\overrightarrow{AB}}\), \(\textcolor{#e9b509}{\overrightarrow{AC}}\) und \(\textcolor{#e9b509}{\overrightarrow{AS}}\) bestimmen (sofern nicht bereits bekannt):
\(A(6|0|4)\), \(B(0|6|4)\), \(C(-6|0|4)\), \(S(0|0|1)\)
\[\textcolor{#e9b509}{\overrightarrow{AB}} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 6 \\ 4 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} = \textcolor{#e9b509}{\begin{pmatrix} -6 \\ 6 \\ 0 \end{pmatrix}}\]
\[\textcolor{#e9b509}{\overrightarrow{AC}} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} -6 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} = \textcolor{#e9b509}{\begin{pmatrix} -12 \\ 0 \\ 0 \end{pmatrix}}\]
\[\textcolor{#e9b509}{\overrightarrow{AS}} = \overrightarrow{S} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} = \textcolor{#e9b509}{\begin{pmatrix} -6 \\ 0 \\ -3 \end{pmatrix}}\]
Volumen der Pyramide \(ABCDS\) berechnen:
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
\[\begin{align*} V_{ABCDS} &= 2 \cdot V_{ABCS} \\[0.8em] &= 2 \cdot \frac{1}{6} \cdot \vert (\textcolor{#e9b509}{\overrightarrow{AB}} \times \textcolor{#e9b509}{\overrightarrow{AC}}) \circ \textcolor{#e9b509}{\overrightarrow{AS}} \vert\\[0.8em] &= \frac{1}{3} \cdot \left| \left[\textcolor{#e9b509}{\begin{pmatrix} -6 \\ 6 \\ 0 \end{pmatrix}} \times \textcolor{#e9b509}{\begin{pmatrix} -12 \\ 0 \\ 0 \end{pmatrix}} \right] \circ \textcolor{#e9b509}{\begin{pmatrix} -6 \\ 0 \\ -3 \end{pmatrix}} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} 6&\cdot&0&-&0&\cdot&0 \\ 0&\cdot&(-12)&-&(-6)&\cdot&0 \\ (-6)&\cdot&0&-&6&\cdot&(-12) \end{pmatrix} \circ \begin{pmatrix} -6 \\ 0 \\ -3 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 72 \end{pmatrix} \circ \begin{pmatrix} -6 \\ 0 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \vert 0 \cdot (-6) + 0 \cdot 0 + 72 \cdot 3 \vert \\[0.8em] &= \frac{1}{\cancel{3}} \cdot 72 \cdot \cancel{3} \\[0.8em] &= 72\end{align*}\]
