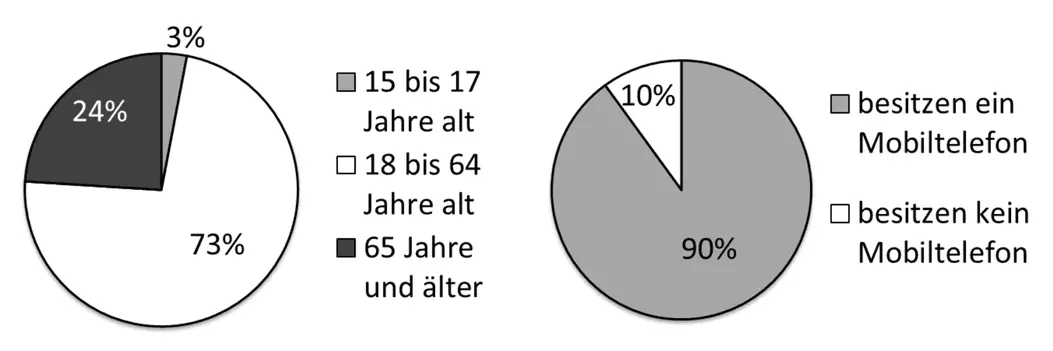
Die beiden Diagramme zeigen für die Bevölkerungsgruppe der über 14-jährigen in Deutschland Daten zur Altersstruktur und zum Besitz von Mobiltelefonen.
Aus den über 14-jährigen in Deutschland wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:
\(M\): „Die Person besitzt ein Mobiltelefon."
\(S\): „Die Person ist 65 Jahre oder älter."
\(E\): „Mindestens eines der Ereignisse \(M\) und \(S\) tritt ein."
Geben Sie an, welche zwei der folgenden Mengen I bis VI jeweils das Ereignis \(E\) beschreiben.
\[\textsf{I}\enspace \, \quad M \cap S\]
\[\textsf{II} \;\, \quad M \cup S\]
\[\textsf{III} \quad \overline{M \cup S}\]
\[\textsf{IV} \quad (M \cap \overline{S}) \cup (\overline{M} \cap S) \cup (\overline{M} \cap \overline{S})\]
\[\textsf{V} \; \quad (M \cap S) \cup (M \cap \overline{S}) \cup (\overline{M} \cap S)\]
\[\textsf{VI} \quad \overline{M \cap S}\]
(2 BE)
Lösung zu Teilaufgabe 1a
Ereignis als Menge beschreiben
\(M\): „Die Person besitzt ein Mobiltelefon."
\(S\): „Die Person ist 65 Jahre oder älter."
\(E\): „Mindestens eines der Ereignisse \(M\) und \(S\) tritt ein."
Das Ereignis \(E\) bedeutet:
- Entweder tritt das Ereignis \(M\) ein (und das Ereignis \(S\) nicht): \(M \cap \overline{S}\),
- oder es tritt das Ereignis \(S\) ein (und das Ereignis \(M\) nicht): \(\overline{M} \cap S\),
- oder beide Ereignisse \(M\) und \(S\) treten zugleich ein: \(M \cap S\).
Das Ereignis \(E\) beschreibt damit die Vereinigungsmenge \(M \cup S\) der Ereignisse \(M\) und \(S\).
\[\begin{align*}E &= M \cup S \\[0.8em] &= (M \cap S) \cup (M \cap \overline{S}) \cup (\overline{M} \cap S) \end{align*}\]
\(\Longrightarrow \quad\) Die Menge II und die Menge V beschreiben jeweils das Ereignis \(E\).


