Erwartungswert, Varianz und Standardabweichung einer Zufallsgröße
Der Erwartungswert, die Varianz und die Standardabweichung einer Zufallsgröße \(X\) sind Kennwerte, welche die Wahrscheinlichkeitsverteilung der Zufallsgröße charakterisieren.
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
Die Varianz \(\boldsymbol{Var(X)}\) und die Standardabweichung \(\boldsymbol{\sigma}\) einer Zufallsgröße \(X\) sind Maßzahlen für die Streuung der Werte \(x_{i}\) der Zufallsgröße um den Erwartungswert \(\mu\).
Erwartungswert, Varianz und Standardabweichung (vgl. Merkhilfe)
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(X\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Varianz \(\boldsymbol{Var(X)}\) der Zufallsgröße \(X\)
\[\begin{align*}Var(X) &= \sum \limits_{i = 1}^{n} (x_{i} - \mu)^{2} \cdot p_{i} \\[0.8em] &= (x_{1} - \mu)^{2} \cdot p_{1} + (x_{2} - \mu)^{2} \cdot p_{2} \,+\, ... \,+\, (x_{n} - \mu)^{2} \cdot p_{n} \end{align*}\]
Standardabweichung \(\boldsymbol{\sigma}\) der Zufallsgröße \(X\)
\[\sigma = \sqrt{Var(X)}\]
Anmerkungen zum Erwartungswert:
Der Erwartungswert \(\mu\) einer Zufallsgröße ist im Allgemeinen kein Wert, den die Zufallsgröße annimmt.
Ein Spiel heißt fair, wenn der Erwartungswert des Gewinns für jeden Spieler gleich null ist.
Anmerkung zur Varianz:
Bei kleiner Varianz liegen die meisten Werte einer Zufallsgröße in der Nähe des Erwartungswerts \(\mu\). Das heißt, die Werte in der Umgebung des Erwartungswerts \(\mu\) treten mit hoher Wahrscheinlichkeit auf. Die Werte, die mehr vom Erwartungswert \(\mu\) abweichen, treten mit geringer Wahrscheinlichkeit auf.
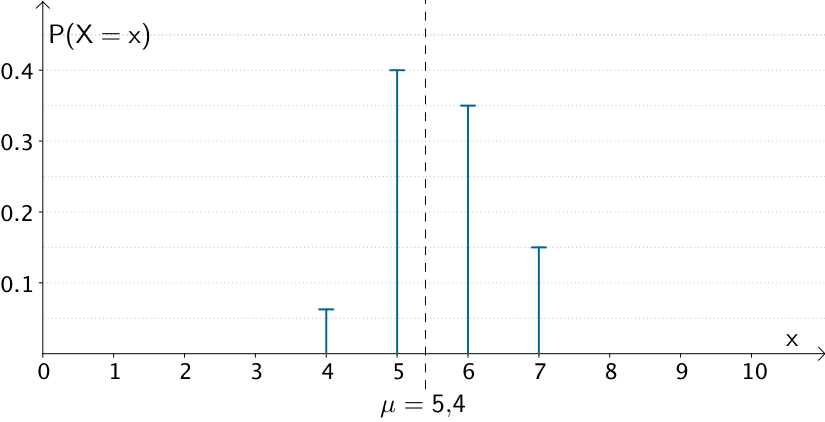
Kleine Varianz: Geringe Streuung der Werte einer Zufallsgröße \(X\) um den Erwartungswert \(\mu = 5{,}4\)
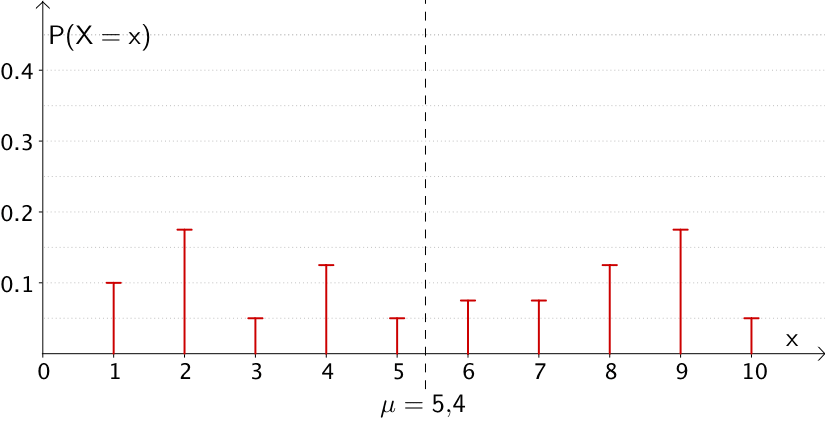
Große Varianz: Starke Streuung der Werte einer Zufallsgröße \(X\) um den Erwartungswert \(\mu = 5{,}4\)
Anmerkung zur Standardabweichung:
Die Standardabweichung \(\sigma\) beschreibt die durchschnittliche (mittlere) Abweichung der Werte einer Zufallsgröße \(X\) von ihrem Erwartungswert \(\mu\).
Im Gegensatz zur Varianz hat die Standardabweichung einer Zufallsgröße \(X\) die gleiche Einheit wie die Werte der Zufallsgröße.
Beispielaufgabe
Für ein Gewinnspiel wird zuerst das Glücksrad 1 und anschließend das Glücksrad 2 gedreht. Wird zweimal weiß gedreht, bekommt der Spieler nichts ausbezahlt. Wird einmal rot gedreht, bekommt der Spieler 1 € ausbezahlt. Dreht der Spieler zweimal rot, werden ihm 7 € ausbezahlt.
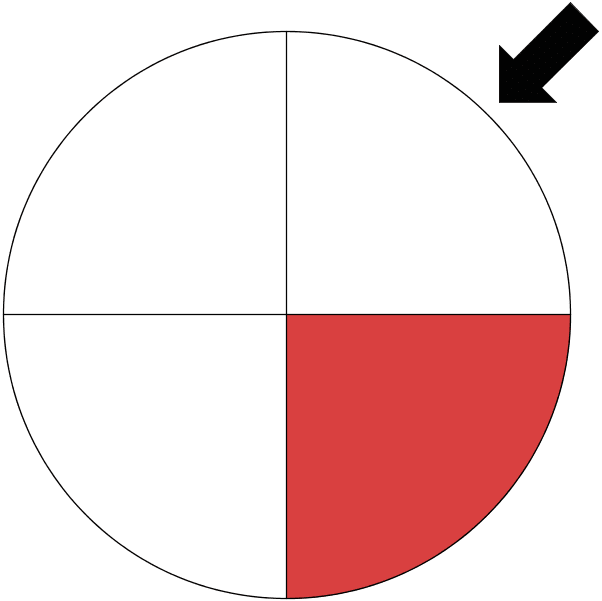Glücksrad 1
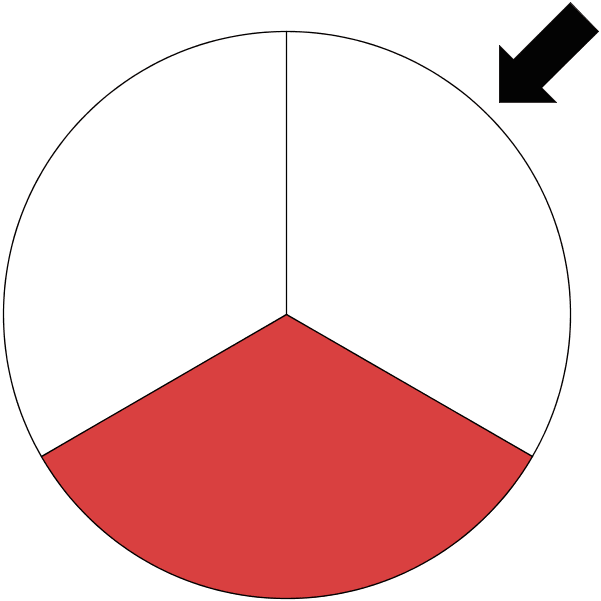Glücksrad 2
a) Der Betreiber des Gewinnspiel möchte im Mittel 2 € pro Spiel einnehmen. Welchen Einsatz muss er verlangen?
b) Der Einsatz pro Spiel beträgt 3 €. Bestimmen Sie Erwartungswert, Varianz und Standardabweichung der Zufallsgröße \(G\): „Gewinn des Spielers in Euro". Erläutern Sie die Bedeutung des Wertes der Standardabweichung der Zufallsgröße \(G\) im Sachzusammenhang.
c) Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(G\) einen Wert innerhalb der einfachen Standardabweichung um den Erwartungswert annimmt. Welche Bedeutung hat diese Wahrscheinlichkeit im Sachzusammenhang?
a) Höhe des Einsatzes, damit der Betreiber des Gewinnspiels im Mittel 2 € pro Spiel einnimmt
Der Betreiber des Gewinnspiels nimmt im Mittel 2 € pro Spiel ein, wenn der Einsatz pro Spiel 2 Euro mehr beträgt als der durchschnittliche Auszahlungsbetrag.
Es sei \(X\) die Zufallsgröße, welche den Auszahlungsbetrag in Euro angibt.
Erwartungswert \(E(X)\) der Zufallsgröße \(X\)
Um den Erwartungswert \(E(X)\) der Zufallsgröße \(X\) berechnen zu können, wird zunächst die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) ermittelt.
Das Gewinnspiel kann als zweistufiges Zufallsexperiment aufgefasst werden. Das Drehen des Glücksrads 1 bildet die erste Stufe und das Drehen des Glücksrads 2 die zweite Stufe. Das Zufallsexperiment lässt sich mithilfe eines Baumdiagramms veranschaulichen (vgl. Abiturskript - 3.1.4 Baumdiagramm und Vierfeldertafel).
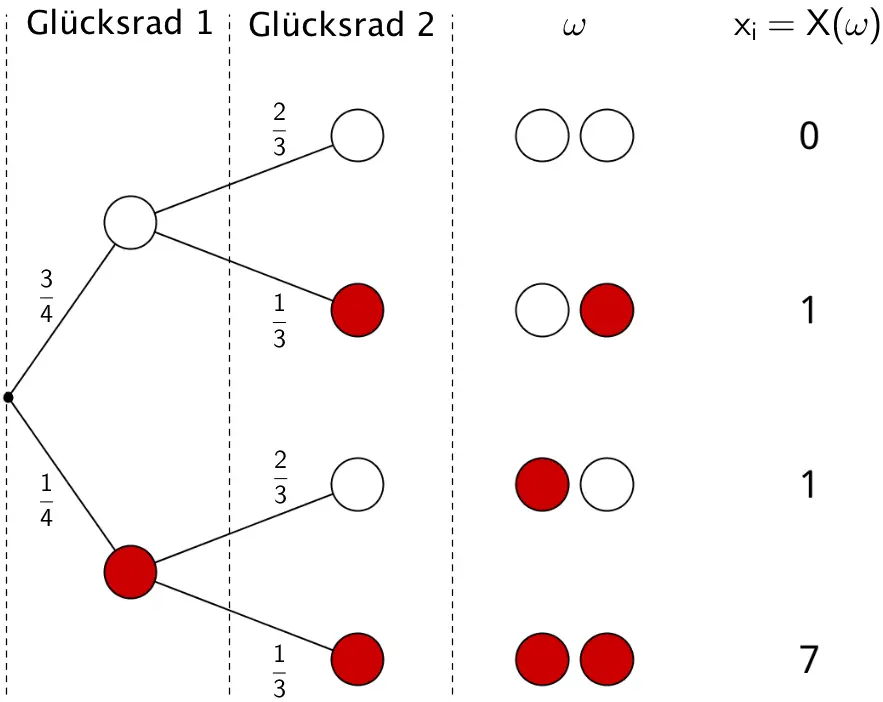
Baumdiagramm des zweistufigen Zufallsexperiments (Gewinnspiel): „Zuerst wird Glücksrad 1 und anschließend Glücksrad 2 gedreht."
Mithilfe der 1. bzw. 2. Pfadregel ergeben sich folgende Wahrscheinlichkeiten \(P(X = x_{i})\) (vgl. Abiturskript - 3.1.4 Baumdiagramm und Vierfeldertafel, Pfadregeln):
\[P(X = 0) = \frac{3}{4} \cdot \frac{2}{3} = \frac{6}{12}\]
\[P(X = 1) = \frac{3}{4} \cdot \frac{1}{3} + \frac{1}{4} \cdot \frac{2}{3} = \frac{3}{12} + \frac{2}{12} = \frac{5}{12}\]
\[P(X = 7) = \frac{1}{4} \cdot \frac{1}{3} = \frac{1}{12}\]
Probe:
Die Summe der Wahrscheinlichkeiten \(P(X = x_{i})\) muss gleich Eins sein.
\[\sum \limits_{i = 1}^{n = 3} P(X = x_{i}) = \frac{6}{12} + \frac{5}{12} + \frac{1}{12} = \frac{12}{12} = 1\]
| \(x_{i}\) | \(0\) | \(1\) | \(7\) |
| \(P(X = x_{i})\) | \(\dfrac{6}{12}\) | \(\dfrac{5}{12}\) | \(\dfrac{1}{12}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Auszahlungsbetrag in Euro"
Erwartungswert \(E(X)\) der Zufallsgröße \(X\) berechnen:
\[\begin{align*}E(X) &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} + x_{3} \cdot p_{3} \\[0.8em] &= 0 \cdot \frac{1}{2} + 1 \cdot \frac{5}{12} + 7 \cdot \frac{1}{12} \\[0.8em] &= \frac{5}{12} + \frac{7}{12} \\[0.8em] &= 1 \end{align*}\]
Im Mittel beträgt der Auszahlungsbetrag pro Spiel 1 €.
Damit der Betreiber des Gewinnspiels pro Spiel 2 € einnimmt, muss er pro Spiel einen Einsatz in Höhe von 3 € verlangen.
b) Erwartungswert, Varianz und Standardabweichung der Zufallsgröße \(G\)
Zufallsgröße \(G\): „Gewinn des Spielers in Euro"
Einsatz pro Spiel: 3 €
\[\text{Gewinn} = \text{Auszahlungsbetrag} - \text{Einsatz}\]
Bei den möglichen Auszahlungsbeträgen in Höhe von 0 €, 1 € oder 7 € und einem Einsatz pro Spiel in Höhe von 3 € können die möglichen Gewinnbeträge (Verlustbeträge) eines Spielers in Höhe von -3 €, -2 € oder 4 € sein. Die Zufallsgröße \(G\) kann also die Werte \(g_{1} = -3\), \(g_{2} = -2\) und \(g_{3} = 4\) annehmen.
| \(g_{i}\) | \(-3\) | \(-2\) | \(4\) |
| \(P(G = g{i})\) | \(\dfrac{6}{12}\) | \(\dfrac{5}{12}\) | \(\dfrac{1}{12}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\): „Gewinn des Spielers in Euro"
Erwartungswert \(E(G)\) der Zufallsgröße \(G\)
\[\begin{align*}\mu = E(G) &= g_{1} \cdot p_{1} + g_{2} \cdot p_{2} + g_{3} \cdot p_{3} \\[0.8em] &= (-3) \cdot \frac{1}{2} + (-2) \cdot \frac{5}{12} + 4 \cdot \frac{1}{12} \\[0.8em] &= -\frac{3}{2} - \frac{10}{12} + \frac{4}{12} \\[0.8em] &= -\frac{24}{12} \\[0.8em] &= - 2 \end{align*}\]
Bei einem Einsatz von 3 € pro Spiel beträgt der Gewinn (Verlust) des Spielers im Mittel -2 € pro Spiel (vgl. Teilaufgabe a).
Varianz \(Var(G)\) der Zufallsgröße \(G\)
\[\begin{align*} Var(G) &= (g_{1} - \mu)^{2} \cdot p_{1} + (g_{2} - \mu)^{2} \cdot p_{2} + (g_{3} - \mu)^{2} \cdot p_{3} \\[0.8em] &= (-3 - (-2))^{2} \cdot \frac{1}{2} + (-2 - (-2))^{2} \cdot \frac{5}{12} + (4 - (-2))^{2} \cdot \frac{1}{12} \\[0.8em] &= \frac{1}{2} + 0 + \frac{36}{12} \\[0.8em] &= 3{,}5 \end{align*}\]
Standardabweichung \(\sigma\) der Zufallsgröße \(G\)
\[\sigma = \sqrt{Var(G)} = \sqrt{3{,}5} \approx 1{,}87\]
Bedeutung im Sachzusammenhang:
Im Mittel weicht der Gewinn des Spielers um ca. 1,87 € vom durchschnittlichen Gewinn -2 € (Verlust) ab.
\[\mu - \sigma = -2 - 1{,}87 = -3{,}87\]
\[\mu + \sigma = -2 + 1{,}87 = -0{,}13\]
Bei einem Einsatz von 3 € pro Spiel verliert ein Spieler im Mittel zwischen 0,13 € und 3,87 € pro Spiel.
c) Wahrscheinlichkeit dafür, dass die Zufallsgröße \(G\) einen Wert innerhalb der einfachen Standardabweichung annimmt
Gesucht ist die Wahrscheinlichkeit dafür, dass der Wert der Zufallsgröße \(G\) im Intervall \(]\mu - \sigma;\mu + \sigma[\) liegt bzw. dafür, dass die Abweichung \(\vert G - \mu \vert\) eines Wertes der Zufallsgröße \(G\) von ihrem Erwartungswert \(\mu\) kleiner als die einfache Standardabweichung \(\sigma\) ist.
\[\vert G - \mu \vert < \sigma\]
\[\begin{align*} P(\vert G - \mu \vert < \sigma) &= P(\mu - \sigma < X < \mu + \sigma) \\[0.8em] &= P(-3{,}87 < X < -0{,}13) \\[0.8em] &= P(-3 \leq X \leq -2) \\[0.8em] &= P(X = -3) + P(X = -2) \\[0.8em] &= \frac{6}{12} + \frac{5}{12} \\[0.8em] &= \frac{11}{12} \\[0.8em] &\approx 0{,}917 \\[0.8em] &= 91{,}7\,\% \end{align*}\]
Bedeutung im Sachzusammenhang:
Bei einem Einsatz von 3 € pro Spiel verliert ein Spieler mit einer Wahrscheinlichkeit von ca. 91,7 % im Mittel zwischen 0,13 € und 3,87 € pro Spiel.
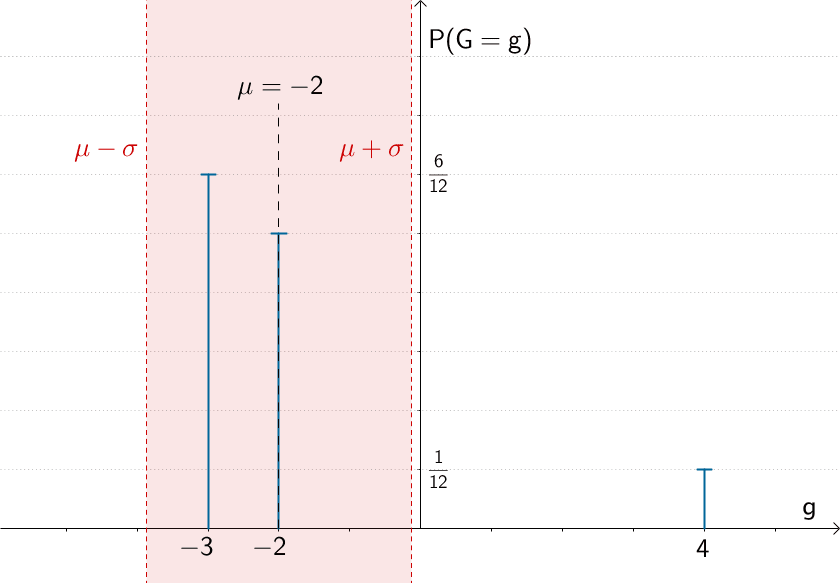
Stabdiagramm der Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\): „Gewinn des Spielers in Euro", Erwartungswert \(\mu\) und Intervall \([\mu - \sigma; \mu + \sigma]\) der einfachen Standardabweichung (Sigma-Umgebung des Erwartungswerts)
