Abbildung 2 zeigt den Graphen \(G_g\) einer in \(\mathbb R \backslash \{1\}\) definierten gebrochen-rationalen Funktion \(g\) mit folgenden Eigenschaften:
-
Die Funktion \(g\) hat in \(x = 1\) eine Polstelle ohne Vorzeichenwechsel;
-
\(G_g\) verläuft stets oberhalb seiner schrägen Asymptote, die durch die Gleichung \(y = \frac{1}{2}x - 1\) gegeben ist;
-
die einzige Nullstelle von \(g\) ist \(x = -1\).
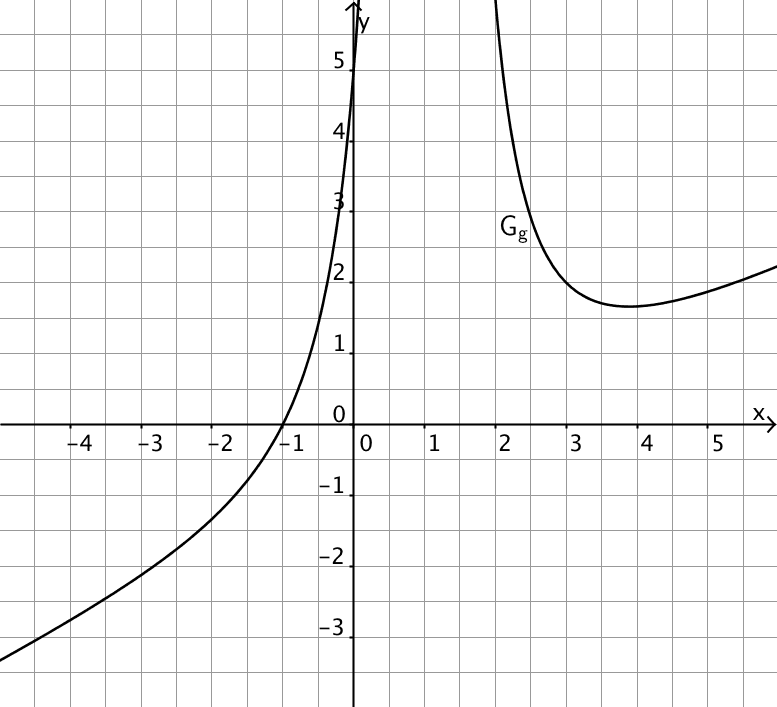 Abb. 2
Abb. 2
Ermitteln Sie mithilfe von Abbildung 2 näherungsweise den Wert der Ableitung \(g'\) von \(g\) an der Stelle \(x = -1\); veranschaulichen Sie Ihr Vorgehen durch geeignete Eintragungen in der Abbildung.
Aus der Gleichung der schrägen Asymptote ergibt sich unmittelbar das Verhalten der Ableitung \(g'\) für \(x \to +\infty\) und \(x \to -\infty\). Geben Sie dieses Verhalten an und skizzieren Sie den Graphen von \(g'\) in Abbildung 2.
(6 BE)
Lösung zu Teilaufgabe 2a
Ermitteln des Wertes der Ableitung \(g'\) von \(g\) an der Stelle \(x = -1\)
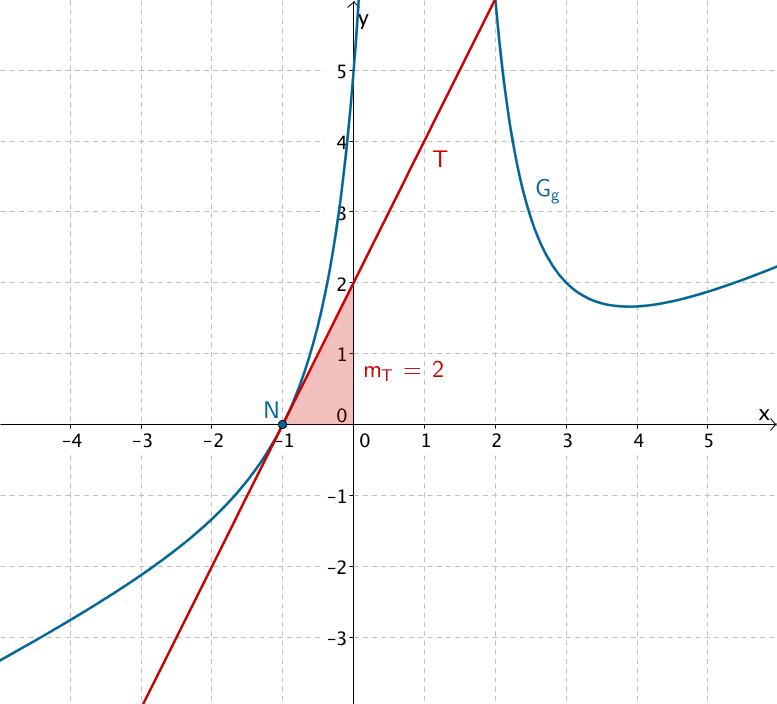
Die Steigung der Tangente \(T\) an \(G_g\) im Punkt \(N(-1|0)\) ist gleich dem Funktionswert der Ableitung \(g'(-1)\).
Man skizziert die Tangente an \(G_g\) im Punkt \(N(-1|0)\) und erhält näherungsweise:
\[m_{T} = \frac{\Delta y}{\Delta x} = \frac{2}{1} = 2 \quad \Longrightarrow \quad g'(-1) = 2\]
Verhalten der Ableitung \(g'\) für \(x \to +\infty\) und \(x \to -\infty\)
Für \(x \to +\infty\) und \(x \to -\infty\) nähert sich der Graph von \(g\) der schrägen Asymptoten \(y = \frac{1}{2}x - 1\). Es gilt:
\[\lim \limits_{x \, \to \, \pm\infty} g(x) = \lim \limits_{x \, \to \, \pm\infty} \left ( \frac{1}{2}x - 1 \right )\]
Dann gilt für das Verhalten der Ableitung \(g'(x)\) im Unendlichen:
\[\lim \limits_{x \, \to \, \pm\infty} g'(x) = \lim \limits_{x \, \to \, \pm\infty} \left ( \frac{1}{2}x - 1 \right )' = \frac{1}{2}\]
\(\Longrightarrow \quad y = \frac{1}{2}\) ist waagrechte Asymptote von \(g'(x)\).
Skizze des Graphen von \(g'\)
Aus Abbildung 2 entnimmt man das Monotonieverhalten von \(g\) und bestimmt damit das Vorzeichen von \(g'\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Im Intervall \(]-\infty;1[\) steigt \(g(x)\) streng monoton. \(\quad \Longrightarrow \quad g'(x) > 0\) für alle \(x \in ]-\infty;1[\)
An der Stelle \(x_T \approx 3{,}9\) zeigt der Graph von \(g\) einen Tiefpunkt. \(\quad \Longrightarrow \quad g'(x_T) = 0\) (Notwendige Bedingung für eine Extremstelle).
Im Intervall \(]1;x_T]\) fällt \(g(x)\) streng monoton. \(\quad \Longrightarrow \quad g'(x) < 0\) für alle \(x \in ]1;x_T]\)
Im Intervall \([x_T;+\infty[\) steigt \(g(x)\) streng monoton. \(\quad \Longrightarrow \quad g'(x) > 0\) für alle \(x \in [x_T;+\infty[\)
\(g'\) besitzt wie \(g\) eine Definitionslücke für \(x = 1\). Für \(x \to 1^-\) steigt \(G_g\) beliebig steil. Für \(x \to 1^+\) fällt \(G_g\) beliebig steil.
\[\Longrightarrow \quad \lim \limits_{x \, \to \, 1^-} g'(x) = + \infty; \qquad \lim \limits_{x \, \to \, 1^+} g'(x) = - \infty\]
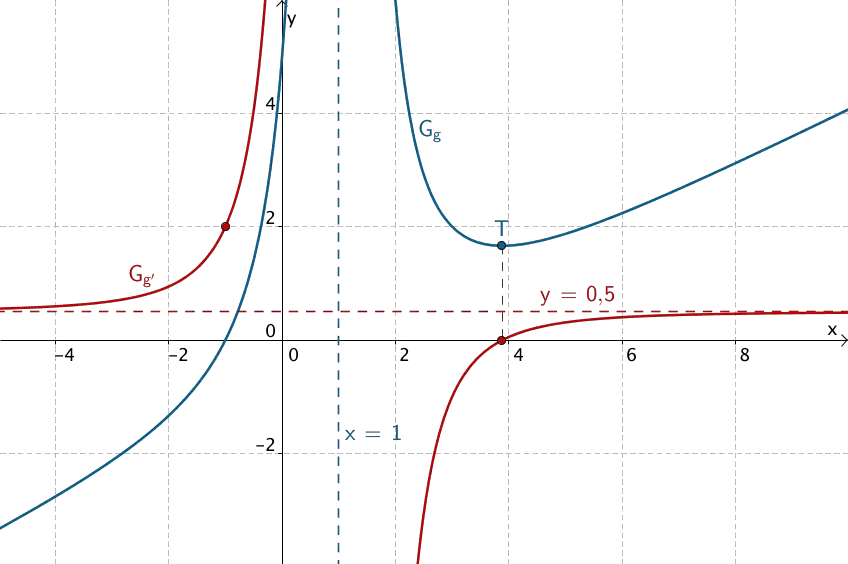
Verlauf des Graphen von \(g'\)

