Auf einem Abschnitt einer wenig befahrenen Landstraße ist eine Höchstgeschwindigkeit von 80 km/h zugelassen. An einer Stelle dieses Abschnitts wird die Geschwindigkeit vorbeifahrender Pkw gemessen. Im Folgenden werden vereinfachend nur solche Fahrten betrachtet, bei denen die Fahrer die Geschwindigkeit unabhängig voneinander wählen konnten.
Für die ersten 200 erfassten Fahrten ergab sich nach Einteilung in Geschwindigkeitsklassen die folgende Verteilung:
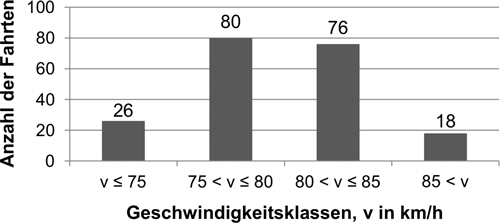
Bei 62 % der 200 Fahrten war der Fahrer allein unterwegs, 65 dieser Alleinfahrer fuhren zu schnell. Aus den 200 Fahrten wird eine zufällig ausgewählt. Es werden folgende Ereignisse betrachtet:
\(A\): „Der Fahrer war allein unterwegs."
\(S\): „Der Pkw war zu schnell."
Weisen Sie nach, dass die Ereignisse \(A\) und \(S\) stochastisch abhängig sind, und geben Sie hierfür einen möglichen Grund im Sachzusammenhang an.
(5 BE)
Lösung zu Teilaufgabe 1a
Gegeben sind folgende Wahrscheinlichkeiten:
\(P(A) = 0{,}62\)
Eine Geschwindigkeit von über 80 km/h gilt als zu schnell.
\(P(S) = P(80 < v \leq 85) + P(85 < v) = \dfrac{76}{200} + \dfrac{18}{200} = \dfrac{94}{200} = 0{,}47\)
\(P(A \cap S) = \dfrac{65}{200} = 0{,}325\)
Stochastische Abhängigkeit der Ereignisse \(A\) und \(S\) nachweisen:
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
\[P(A) \cdot P(S) = 0{,}62 \cdot 0{,}47 = 0{,}2914 \neq 0{,}325 = P(A \cap S)\]
Also sind die Ereignisse \(A\) und \(S\) stochastisch abhängig.
Möglicher Grund im Sachzusammenhang:
Die Anwesenheit eines Bei- bzw. Mitfahrers beeinflusst die Fahrweise des Fahrers, beispielsweise indem er diesen unachtsam für die zugelassene Höchstgeschwindigkeit werden lässt.
Anmerkung:
Da \(P(A) \cdot P(S) < P(A \cap S)\) gilt, muss in diesem Fall angenommen werden, dass ein Bei- bzw. Mitfahrer den Fahrer dazu verleitet, schneller als erlaubt zu fahren.


