Anlässlich einer Studie wurden 300 weibliche und 700 männliche Bewohner einer Großstadt im Alter von 18 bis 30 Jahren dazu befragt, ob sie Interesse an Car-Sharing haben. 20 % der Befragten waren weiblich und gaben an, nicht interessiert zu sein. 8 % der Befragten waren männlich und gaben an, Interesse an Car-Sharing zu haben. Das Kreisdiagramm veranschaulicht die absoluten Häufigkeiten, die sich bei der Befragung ergaben.
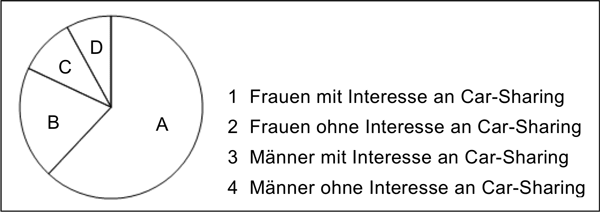
Ordnen Sie die Beschriftungen 1 bis 4 den Sektoren A bis D korrekt zu und begründen Sie Ihre Zuordnung.
(4 BE)
Lösung zu Teilaufgabe 1a
Betrachtet werden folgende Ereignisse:
\(\textcolor{#cc071e}{1 \enspace F \cap C}\): „Frau mit Interesse an Car-Sharing"
\(\textcolor{#0087c1}{2 \enspace F \cap \overline{C}}\): „Frau ohne Interesse an Car-Sharing"
\(\textcolor{#89ba17}{3 \enspace M \cap C}\): „Mann mit Interesse an Car-Sharing“
\(\textcolor{#e9b509}{4 \enspace M \cap \overline{C}}\): „Mann ohne Interesse an Car-Sharing“
Die Zuordnung erfolgt beispielsweise durch Berechnung der absoluten Häufigkeiten der Ereignisse und anschließendem Vergleich mit der Größe der Sektoren.
\[\vert F \vert = 300\]
\[\vert M \vert = 700\]
\[\vert \Omega \vert = \vert F \vert + \vert M \vert = 300 + 700 = 1000\]
\[\textcolor{#0087c1}{2 \enspace \vert F \cap \overline{C} \vert} = 0{,}2 \cdot \vert \Omega \vert = 0{,}2 \cdot 1000 = \textcolor{#0087c1}{200}\]
\[\textcolor{#cc071e}{1 \enspace \vert F \cap C \vert} = \vert F \vert - \vert F \cap \overline{C} \vert = 300 - 200 = \textcolor{#cc071e}{100}\]
\[\textcolor{#89ba17}{3 \enspace \vert M \cap C \vert} = 0{,}08 \cdot \vert \Omega \vert = 0{,}08 \cdot 1000 = \textcolor{#89ba17}{80}\]
\[\textcolor{#e9b509}{4 \enspace \vert M \cap \overline{C} \vert} = \vert M \vert - \vert M \cap C \vert = 700 - 80 = \textcolor{#e9b509}{620}\]
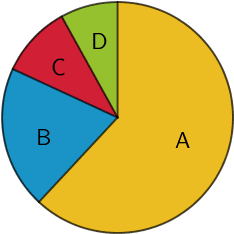
\[\Longrightarrow \quad \textcolor{#cc071e}{1}C,\; \textcolor{#0087c1}{2}B, \; \textcolor{#89ba17}{3}D,\; \textcolor{#e9b509}{4}A\]


