Die Punkte \(M\) und \(N\) liegen auf der Geraden
\(\displaystyle \overrightarrow{X} = \begin{pmatrix} 4{,}8 \\ 8 \\ 7{,}4 \end{pmatrix} + \mu \cdot \begin{pmatrix} 6 \\ 0 \\ -1 \end{pmatrix}\), \(\mu \in \mathbb R\),
die im Modell die Neigung der Dachfläche der Gaube festlegt. Die zur \(x_3\)-Achse parallele Strecke \([NL]\) stellt im Modell den sogenannten Gaubenstiel dar; dessen Länge soll 1,4 m betragen. Um die Koordinaten von \(N\) und \(L\) zu bestimmen, wird die Ebene \(F\) betrachtet, die durch Verschiebung von \(E\) um 1,4 in positive \(x_3\)-Richtung entsteht.
Begründen Sie, dass \(3x_1 + 4x_3 - 49{,}6 = 0\) eine Gleichung von \(F\) ist.
(3 BE)
Lösung zu Teilaufgabe e
\[E\,\colon\,3x_{1} + 4x_{3} - 44 = 0\]
\[F\,\colon\,3x_{1} + 4x_{3} - 49{,}6 = 0\]
Da die Ebene \(F\) aus der Ebene \(E\) durch Verschiebung in \(x_{3}\)-Richtung hervorgeht, sind die beiden Ebenen zueinander parallel.
\[E \parallel F \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \overrightarrow{n}_{F}\]
1. Lösungsansatz: Ebenengleichung in Normalenform in Vektordarstellung
Die Punkte \(B\), \(C\), \(G\), \(H\) und \(T\) liegen in der Ebene \(E\). Dann liegt beispielsweise der um 1,4 in \(x_{3}\)-Richtung verschobene Punkt \(C'\) in der Ebene \(F\).
\[C\,(8|10|5) \quad \xmapsto{\begin{pmatrix} 0 \\ 0 \\ 1{,}4 \end{pmatrix}} \quad C'\,(8|10|6{,}4)\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
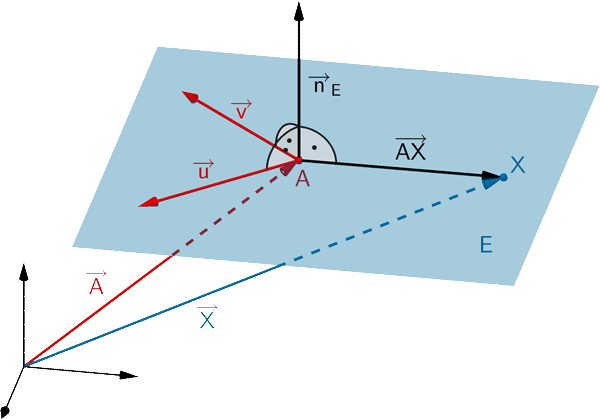
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[\begin{align*} F\,\colon & & \overrightarrow{n}_{F} \circ \bigg( \overrightarrow{X} - \overrightarrow{C'} \bigg) &= 0 \\[0.8em] & & \begin{pmatrix} 3 \\ 0 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 8 \\ 10 \\ 6{,}4 \end{pmatrix} \right] &= 0 \\[0.8em] & & 3 \cdot (x_{1} - 8) + 0 \cdot (x_{2} - 10) + 4 \cdot (x_{3} - 6{,}4) &= 0 \\[0.8em] & & 3x_{1} - 24 + 4x_{3} - 25{,}6 &= 0 \\[0.8em] & & 3x_{1} + 4x_{3} - 49{,}6 &= 0 \end{align*}\]
2. Lösungsansatz: Ebenengleichung in Normalenform in Koordinatendarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\(C'(8|10|6{,}4) \in F\) (siehe 1. Lösungsansatz)
\[F\,\colon\, 3x_{1} + 4x_{3} + n_{0} = 0\]
\[\begin{align*} C' \in F\,\colon\, 3 \cdot 8 + 4 \cdot 6{,}4 + n_{0} &= 0 \\[0.8em] 24 + 25{,}6 + n_{0} &= 0 \\[0.8em] 49{,}6 + n_{0} &= 0 & &| - 49{,}6 \\[0.8em] n_{0} &= -49{,}6 \end{align*}\]
\[F\,\colon\, 3x_{1} + 4x_{3} - 49{,}6 = 0\]


