Gegeben ist die Funktion \(f \colon x \mapsto \displaystyle \frac{2e^x}{e^x + 9}\) mit Definitionsbereich \(\mathbb R\). Abbildung 2 zeigt den Graphen \(G_f\) von \(f\,\).

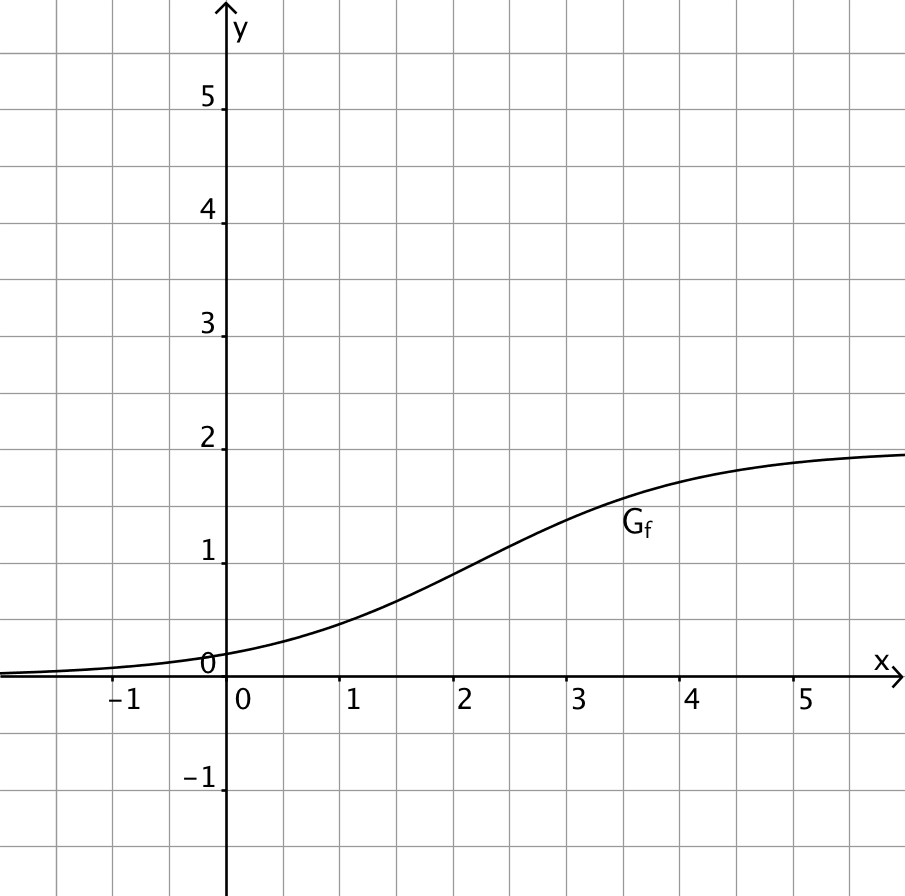Abbildung 2: Graph von fAbb. 2

Zeigen Sie rechnerisch, dass \(G_f\) genau einen Achsenschnittpunkt \(S\) besitzt, und geben Sie die Koordinaten von \(S\) an.

(2 BE)

Lösung zu Teilaufgabe 1a

 

\[f(x) = \frac{2e^x}{e^x + 9}\,; \quad D_f = \mathbb R \]

 

Schnittpunkte mit der \(x\)-Achse untersuchen:

 

\(f(x) = 0 \quad \Longrightarrow \quad\) Zählerterm \(\,2e^x > 0\)

 

\(\Longrightarrow \quad G_f\) besitzt keinen Schnittpunkt mit der \(x\)-Achse (keine Nullstelle).

 

Schnittpunkte mit der \(y\)-Achse untersuchen:

 

\[f(0) = \frac{2e^0}{e^0 + 9} = \frac{2}{10} = 0{,}2\]

 

\(\Longrightarrow \quad S\,(0|0{,}2)\,\) ist einziger Achsenschnittpunkt von \(G_f\,\).

 

Einziger Achsenschnittpunkt S des Graphen von f mit der y-Achse

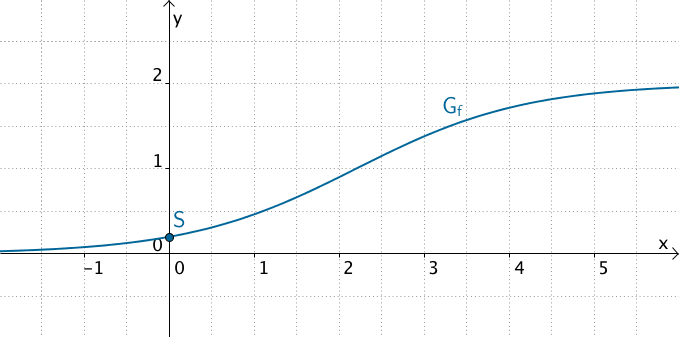
Einziger Achsenschnittpunkt \(\,S\,\) von \(\,G_f\,\) mit der \(y\)-Achse