Die Gerade mit der Gleichung \(y = 1{,}1\) teilt im Modell den vom Kunstwerk eingenommenen Teil der Wand in zwei unterschiedlich gestaltete Bereiche. Beschreiben Sie, wie man mithilfe der Funktion \(q\) das Verhältnis der Flächeninhalte dieser beiden Bereiche näherungsweise bestimmen kann. Geben Sie dazu geeignete Ansätze an und kommentieren Sie diese.
(4 BE)
Lösung zu Teilaufgabe 1f
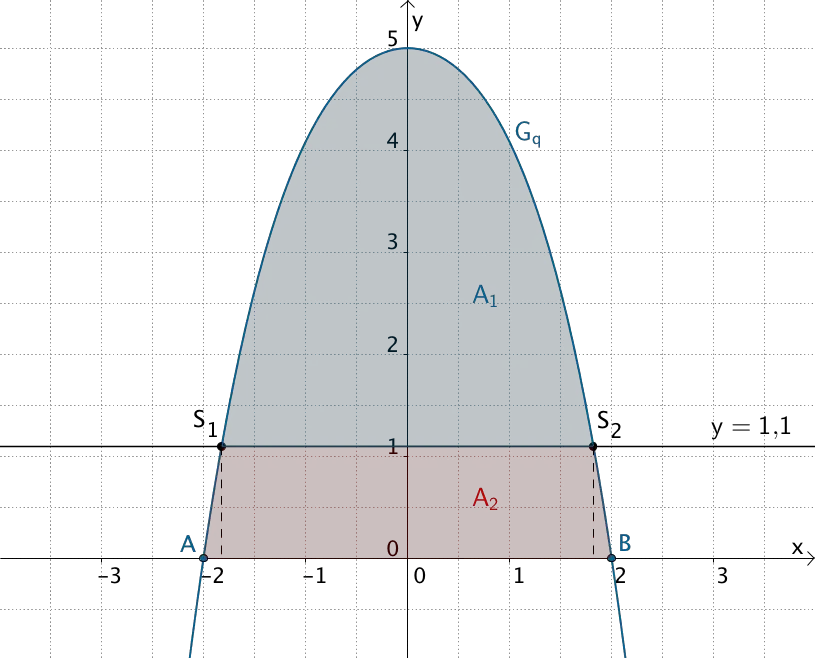
Die Gerade \(y = 1{,}1\,\) teilt den Flächeninhalt \(\,A\,\) (siehe Teilaufgabe 1e) in die Flächeninhalte \(\,A_1\,\) und \(\,A_2\,\).
Um das Verhältnis der Flächeninhalte der Teilflächen \(A_1\) und \(A_2\) bestimmen zu können, genügt es, den Flächeninhalt einer der beiden Teilflächen zu ermitteln. Die Differenz des Flächeninhalts \(A\) (siehe Teilaufgabe e) und des Flächeninhalts einer Teilfläche ergibt den Flächeninhalt der anderen Teilfläche.
Lösungsansatz 1: Flächeninhalt von \(A_1\) zuerst berechnen
a) Schnittstellen der Geraden \(y = 1{,}1\) und \(G_q\) bestimmen
Die Schnittstellen \(x_{S_1}\) und \(x_{S_2}\) beschreiben die Integrationsgrenzen für die Berechnung des Flächeninhalts \(A_1\) durch Integration.
\[q \cap g\,\colon \enspace -0{,}11x^4 - 0{,}81x^2 + 5 = 1{,}1 \quad | \;\text{Substitution:} \; u = x^2 \]
\[\Longrightarrow \quad x_{S_1}\,, \; x_{S_2}\]
b) Flächeninhalt \(A_1\) berechnen
Der Flächeninhalt \(A_1\) des Flächenstücks, das \(G_q\) mit der Geraden \(y = 1{,}1\) einschließt, lässt sich durch Integration berechnen.
\[A_1 = \int_{x_{S_1}}^{x_{S_2}} (q(x) - 1{,}1)\,dx\]
c) Verhältnis der Flächeninhalte \(A_1\) und \(A_2\) bestimmen
Der Flächeninhalt \(A\) (siehe Teilaufgabe 1e) abzüglich des Flächeninhalts \(A_1\) ergibt den Flächeninhalt \(A_2\,\).
\(\displaystyle \frac{A_1}{A_2} = \frac{A_1}{A - A_1} \quad\) oder \(\quad \displaystyle \frac{A_2}{A_1} = \frac{A - A_1}{A_1}\)
Lösungsansatz 2: Flächeninhalt von \(A_2\) zuerst berechnen
a) Schnittstellen der Geraden \(y = 1{,}1\) und \(G_q\) bestimmen
Identische Vorgehensweise wie bei Lösungsansatz 1
b) Flächeninhalt \(A_2\) berechnen
Der Flächeninhalt \(A_2\) des Flächenstücks, das \(G_q\) mit der Geraden \(y = 1{,}1\) und der \(x\)-Achse einschließt lässt sich als Summe von drei Teilflächeninhalten berechnen:
- Flächeninhalt des Flächenstücks, das \(G_q\) mit der \(x\)-Achse und der Geraden \(x = x_{S_1}\) einschließt,
- Flächeninhalt des Rechtecks, das die Gerade \(y = 1{,}1\) mit den Geraden \(x = x_{S_1}\) und \(x = x_{S_2}\) sowie der \(x\)-Achse einschließt und
- Flächeninhalt des Flächenstücks, das \(G_q\) mit der \(x\)-Achse und der Geraden \(x = x_{S_2}\) einschließt.
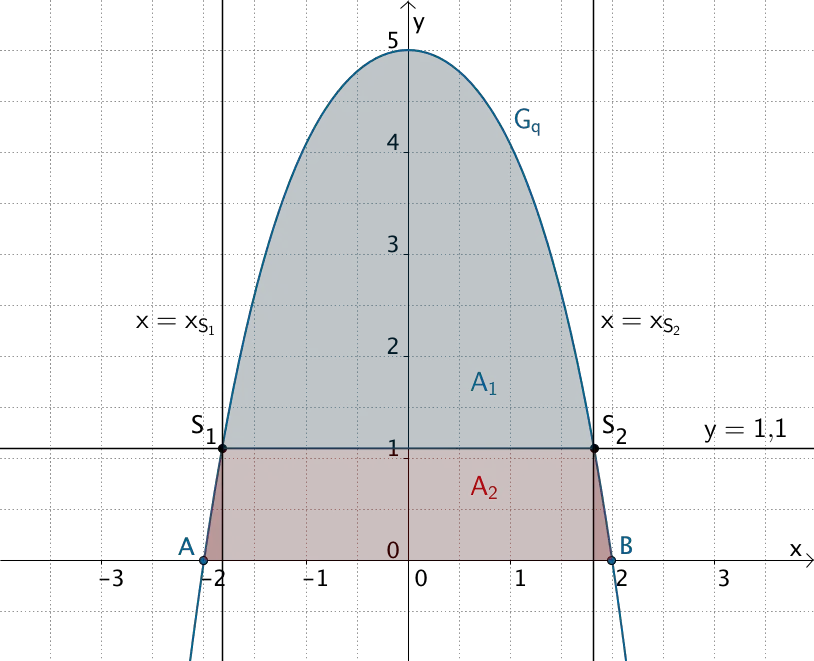
Aufteilung des Flächeninhalts \(A_2\) in drei Teilflächeninhalte. Aufgrund der Achsensymmetrie von \(G_q\) (siehe Teilaufgabe 1b) sind der linke und der rechte Teilflächeninhalt von \(A_2\) gleich groß.
\[\begin{align*} A_2 &= \int_{-2}^{x_{S_1}}q(x)\,dx + (x_{S_2} - x_{S_1}) \cdot 1{,}1 + \int_{x_{S_2}}^{2} q(x)\,dx \\[0.8em] &= 2 \cdot \int_{-2}^{x_{S_1}}q(x)\,dx + (x_{S_2} - x_{S_1}) \cdot 1{,}1 \end{align*}\]
c) Verhältnis der Flächeninhalte \(A_1\) und \(A_2\) bestimmen
Analoge Vorgehensweise wie bei Lösungsansatz 1:
\(\displaystyle \frac{A_1}{A_2} = \frac{A - A_2}{A_2} \quad\) oder \(\quad \displaystyle \frac{A_2}{A_1} = \frac{A_2}{A - A_2}\)


