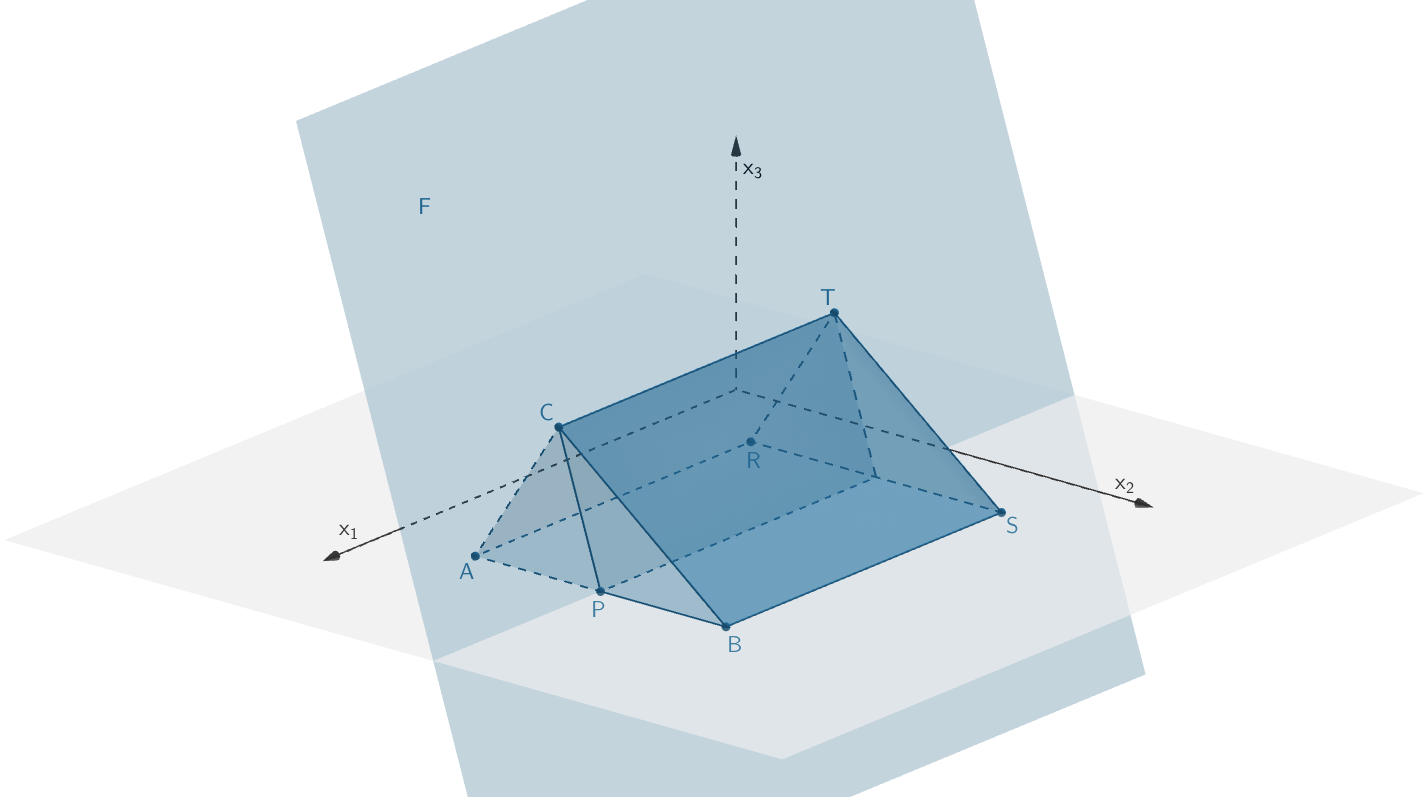
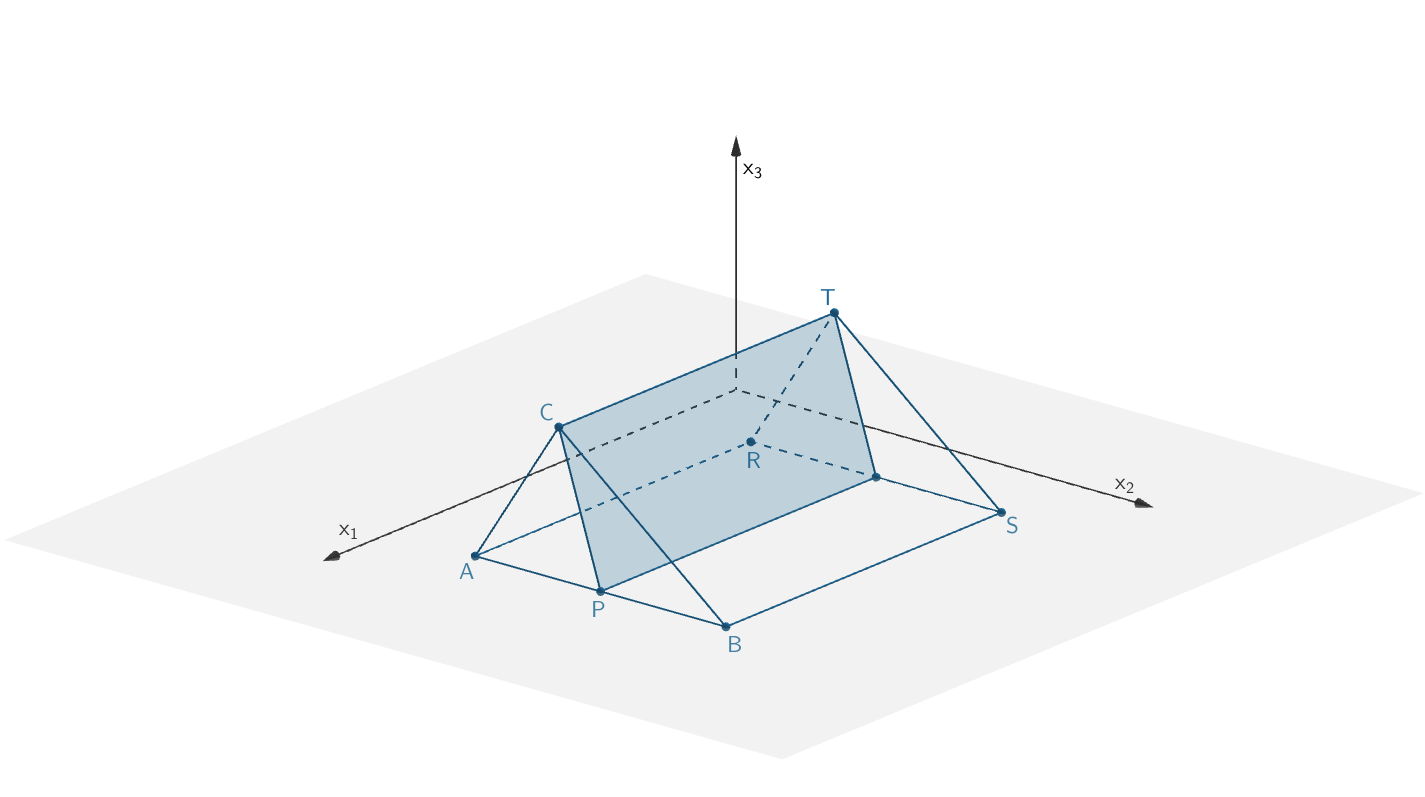
Die Ebene \(F\) enthält die Gerade \(CT\) und zerlegt das Prisma in zwei volumengleiche Teilkörper. Wählen Sie einen Punkt \(P\) so, dass er gemeinsam mit den Punkten \(C\) und \(T\) die Ebene \(F\) festlegt; begründen Sie Ihre Wahl. Tragen Sie die Schnittfigur von \(F\) mit dem Prisma in Ihre Zeichnung ein.
(3 BE)
Lösung zu Teilaufgabe d
Wahl des Punktes \(P\) mit Begründung
Die Ebene \(F\) schneidet die Seitenkanten \([AB]\) und \([RS]\,\). Die entstehenden Teilkörper sind zwei Prismen gleicher Höhe \(h = \overline{CT}\,\). Folglich sind die Volumina der beiden Prismen gleich groß, wenn deren Grundflächen gleich groß sind.
Die Ebene \(F\) teilt die Grundfläche \(ABC\) (bzw. die Deckfläche \(RST\,\)) des Prismas \(ABCRST\) dann in zwei flächengleiche Dreiecke, wenn sie die Seitenhalbierende \([CM_{AB}]\) des Dreiecks \(ABC\,\) (bzw. \([TM_{RS}]\) des Dreiecks \(RST\,\)) enthält.
Besondere Linien und Punkte eines Dreiecks:
Seitenhalbierende
Die Seitenhalbierenden eines Dreiecks verbinden jeweils den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt. Sie schneiden sich im Schwerpunkt des Dreiecks.
Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2 : 1.
Die Seitenhalbierenden teilen ein Dreieck jeweils in zwei flächengleiche Dreiecke.
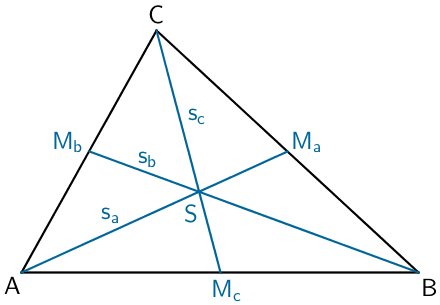
Betrachtung der Grundfläche \(ABC\,\):
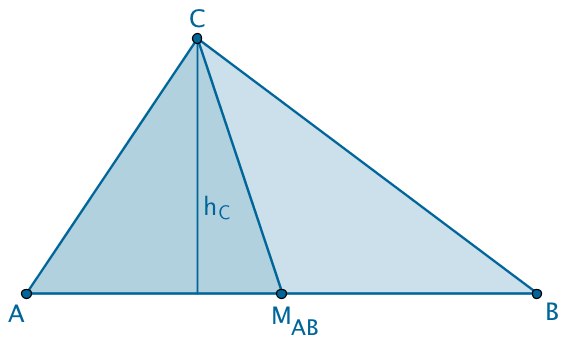
Die Seitenhalbierende \(\,[CM_{AB}]\,\) teilt die Grundfläche \(\,ABC\,\) in die beiden flächengleichen Dreiecke \(\,AM_{AB}C\,\) und \(\,M_{AB}BC\,\).
\[\left. \begin{align*} A_{AM_{AB}C} &= \frac{1}{2} \cdot \overline{AM_{AB}} \cdot h_C \\[0.8em] A_{M_{AB}BC} &= \frac{1}{2} \cdot \overline{M_{AB}B} \cdot h_C \\[0.8em] \overline{AM_{AB}} &= \overline{M_{AB}B} \end{align*} \right\} \Longrightarrow \quad A_{AM_{AB}C} = A_{M_{AB}BC} \]
\(\Longrightarrow \quad\) Der Punkt \(P\) ist Mittelpunkt der Strecke \([AB]\) (bzw. der Strecke \([RS]\,\)).
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*}\overrightarrow{P} &= \overrightarrow{M}_{AB} \\[0.8em] &= \frac{1}{2} \cdot (\overrightarrow{A} + \overrightarrow{B}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 10 \\ 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 10 \\ 8 \\ 0 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 20 \\ 10 \\ 0 \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 0 \end{pmatrix} \quad \Longrightarrow \quad P\,(10|5|0) \end{align*}\]
Schnittfigur der Ebene \(F\) mit dem Prisma \(ABCRST\)
Einzeichnen der Schnittfigur von \(F\) mit dem Prisma

Schnittfigur der Ebene \(F\) mit dem Prisma \(ABCRST\)