Welche künftige Entwicklung der Bevölkerungszahl ist auf der Grundlage des Modells zu erwarten? Begründen Sie Ihre Antwort.
(2 BE)
Lösung zu Teilaufgabe 3b
\[g_{1{,}4} = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]
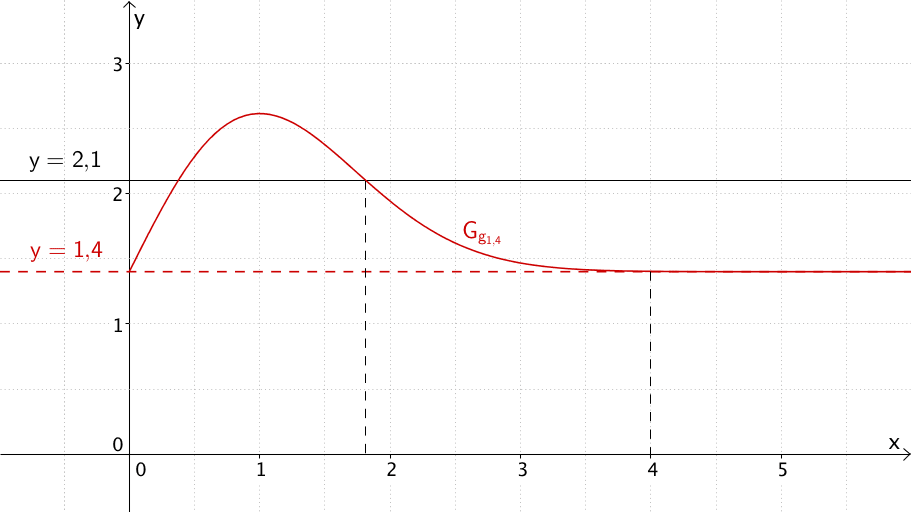
Graph der Funktion \(g_{1{,}4}\) für \(x \geq 0\)
Aus Teilaufgabe 1a bzw. 2a ist bekannt:
\[\lim \limits_{x \, \to \, + \infty} g_c(x) = c\]
\[\Longrightarrow \quad \lim \limits_{x \, \to \, + \infty} g_{1{,}4} = 1{,}4\]
Der Graph von \(g_{1{,}4}\) fällt für \(x > 1\) streng monoton und nähert sich für \(x \to + \infty\) der waagrechten Asymptote \(y = 1{,}4\) an.
Aus Teilaufgabe 3a ist bekannt:
\(g_{1{,}4} < 2{,}1\) für \(x \gtrapprox 1{,}8\)
Nach dem Jahr 1973 sinkt die Geburtenziffer unter den „kritischen Wert" 2,1.
Zu erwartende künftige Entwicklung der Bevölkerungszahl:
Nach dem Jahr 1973 \((x \approx 1{,}8)\) unterschreitet die Geburtenziffer den Wert 2,1 und nimmt anschließend kontinuierlich ab bis sie etwa ab dem Jahr 1995 \((x = 4)\) den annähernd konstanten Wert 1,4 erreicht. Gemäß Angabe ist eine Geburtenziffer von mindestens 2,1 erforderlich, damit die Bevölkerungsanzahl im betrachteten europäischen Land langfristig konstant bleibt. Somit sinkt die Bevölkerungszahl in diesem Land bereits ab dem Jahr 1974. Für die Zukunft ist ebenfalls eine Abnahme der Bevölkerungsanzahl in diesem Land zu erwarten.


