Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massivem Beton, der die Form eines Spats hat. Alle Seitenflächen eines Spats sind Parallelogramme.
In einem Modell lässt sich der Grundkörper durch einen Spat \(ABCDPQRS\) mit \(A\,(28|0|0)\), \(B\,(28|10|0)\), \(D\,(20|0|6)\) und \(P\,(0|0|0)\) beschreiben (vgl. Abbildung). Die rechteckige Grundfläche \(ABQP\) liegt in der \(x_1x_2\)-Ebene. Im Koordinatensystem entspricht eine Längeneinheit 0,1 m, d.h. der Grundkörper ist 0,6 m hoch.
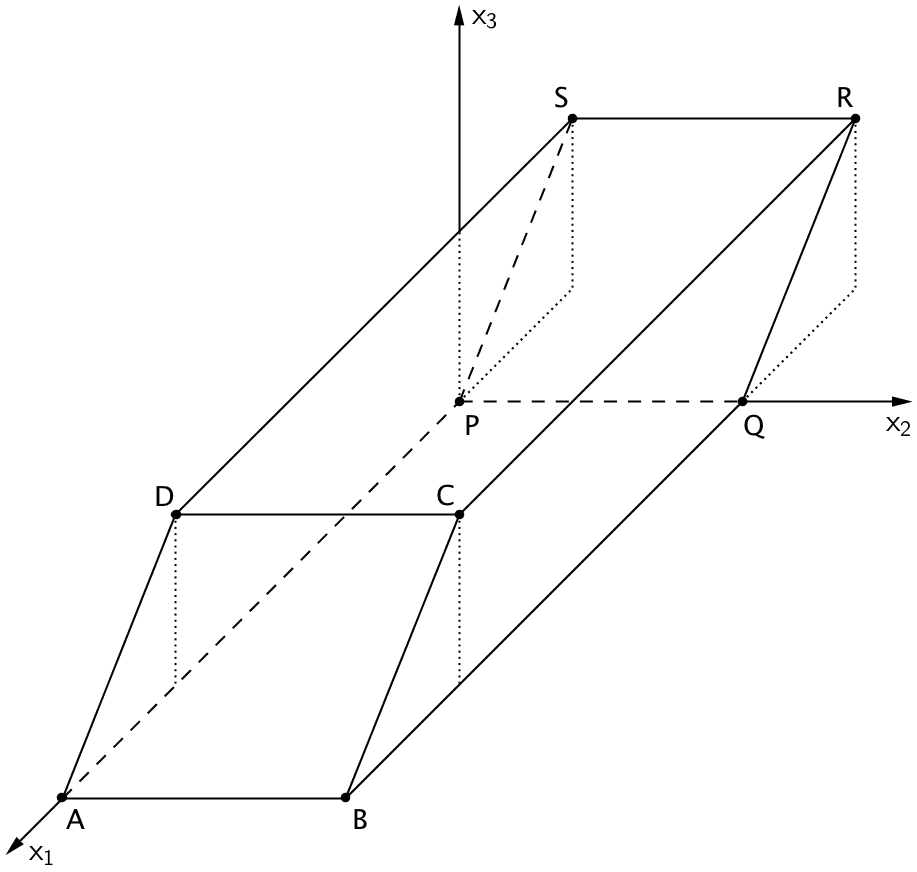
Geben Sie die Koordinaten des Punkts \(C\) an und zeigen Sie, dass die Seitenfläche \(ABCD\) ein Quadrat ist.
(5 BE)
Lösung zu Teilaufgabe a
\[A\,(28|0|0)\,,\enspace B\,(28|10|0)\,,\enspace D\,(20|0|6)\,,\enspace P\,(0|0|0)\]
Koordinaten des Punktes \(C\)
1. Lösungsansatz: Vektoraddition
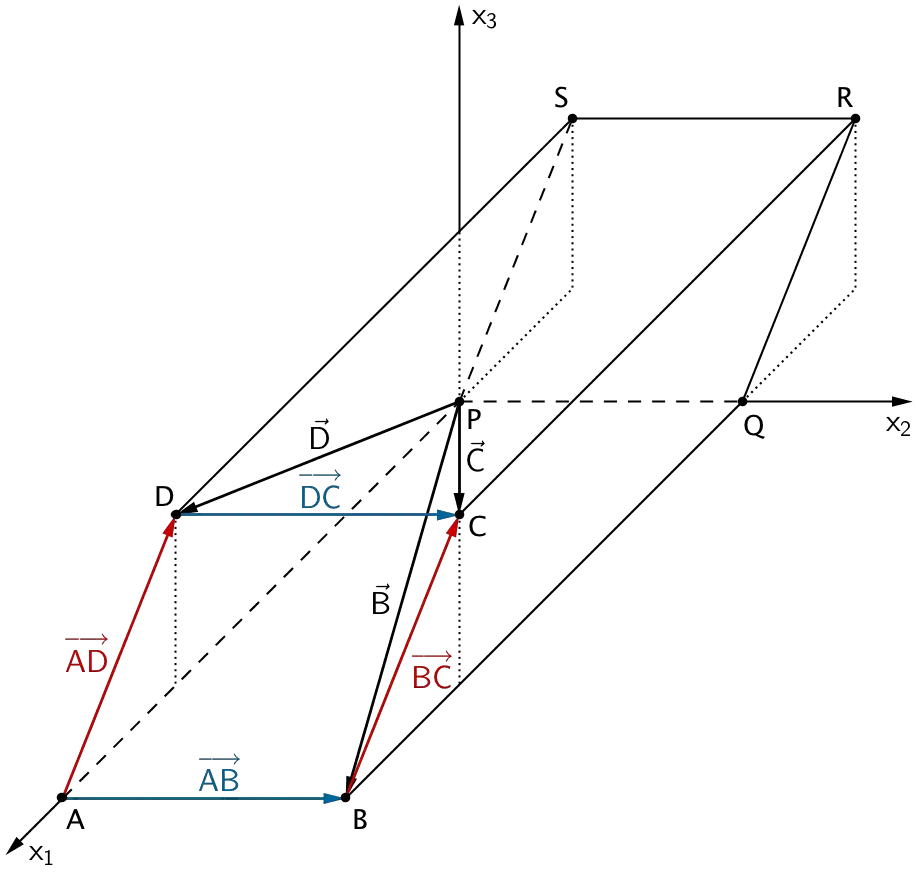
Die Koordinaten des Punktes \(C\) lassen sich durch Vektoraddition berechnen.
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{D} + \overrightarrow{DC} & &| \; \overrightarrow{DC} = \overrightarrow{AB} \\[0.8em] &= \overrightarrow{D} + \overrightarrow{AB} \end{align*}\]
oder
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{B} + \overrightarrow{BC} & &| \; \overrightarrow{BC} = \overrightarrow{AD} \\[0.8em] &= \overrightarrow{B} + \overrightarrow{AD} \end{align*}\]
Vektor \(\overrightarrow{AB}\) bzw. \(\overrightarrow{AD}\) bestimmen:
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 28 \\ 10 \\ 0 \end{pmatrix} - \begin{pmatrix} 28 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} 20 \\ 0 \\ 6 \end{pmatrix} - \begin{pmatrix} 28 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix}\]
Koordinaten des Punktes \(C\) berechnen:
\[ \overrightarrow{C} = \overrightarrow{D} + \overrightarrow{AB} = \begin{pmatrix} 20 \\ 0 \\ 6 \end{pmatrix} + \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix} = \begin{pmatrix} 20 \\ 10 \\ 6 \end{pmatrix}\]
oder
\[\overrightarrow{C} = \overrightarrow{B} + \overrightarrow{AD} = \begin{pmatrix} 28 \\ 10 \\ 0 \end{pmatrix} + \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix} = \begin{pmatrix} 20 \\ 10 \\ 6 \end{pmatrix}\]
\[\Longrightarrow \quad C\,(20|10|6)\]
2. Lösungsansatz: Argumentation mithilfe der Skizze und der Angabe

\[A\,(28|0|0)\,,\enspace B\,(28|10|0)\,,\enspace D\,(20|0|6)\,,\enspace P\,(0|0|0)\]
Der Skizze sowie dem Text der Angabe entnimmt man folgende mathematische Sachverhalte:
\[[AB] \parallel x_2\text{-Achse}\]
\[[AD] \in x_1x_3\text{-Ebene}\]
Parallelogramm \(ABCD \quad \Longrightarrow \quad [DC] \parallel x_2\text{-Achse}\)
\[\begin{align*} \Longrightarrow \quad x_{1_C} &= x_{1_D} = 20 \\[0.8em] x_{2_C} &= x_{2_B} = 10 \\[0.8em] x_{3_C} &= x_{3_D} =6 \end{align*}\]
\[\Longrightarrow \quad D\,(20|10|6)\]
Nachweis, dass die Seitenfläche \(ABCD\) ein Quadrat ist
Die Seitenfläche \(ABCD\) ist ein Quadrat, wenn zwei anliegende Seiten gleich lang sind und senkrecht zueinander stehen.
Länge zweier anliegender Seiten berechnen:
z.B. Länge der Seite \([AB]\) und Länge der Seite \([AD]\)
\(\displaystyle \overrightarrow{AB} = \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix}; \enspace \overrightarrow{AD} = \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix}\) (siehe oben)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{AB} = \vert \overrightarrow{AB} \vert = \left| \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix} \right| = \sqrt{0^2 + 10^2 + 0^2} = 10\]
\[\overline{AD} = \vert \overrightarrow{AD} \vert = \left| \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix} \right| = \sqrt{(-8)^2 + 0^2 + 6^2} = 10\]
\[\Longrightarrow \quad \overline{AB} = \overline{AD}\]
Orthogonalität zweier anliegernder Seiten überprüfen:
![Orthogonalität der Seiten [AB] und [AD] Orthogonalität der Seiten [AB] und [AD]](/images/stories/B2013_G_I/B2013_G_I_1a_02.png)
z.B. Orthogonalität der Seiten \([AB]\) und \([AD]\)
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\(\displaystyle \overrightarrow{AB} = \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix}; \enspace \overrightarrow{AD} = \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix}\) (siehe oben)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\overrightarrow{AB} \circ \overrightarrow{AD} &= \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix} \circ \begin{pmatrix} -8 \\0 \\ 6 \end{pmatrix} \\[0.8em] &= 0 \cdot (-8) + 10 \cdot 0 + 0 \cdot 6 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{AB} \perp \overrightarrow{AD} \quad \Longrightarrow \quad [AB] \perp [AD]\]
\(\Longrightarrow \quad\) Die Seitenfläche \(ABCD\) ist ein Quadrat.


