Zeigen Sie, dass dieser Abstand mit der minimalen Entfernung des Hubschraubers vom Mittelpunkt des Grundstücks übereinstimmt, der im Modell durch den Punkt \(M(-40|30|30)\) dargestellt wird.
(5 BE)
Lösung zu Teilaufgabe e
1. Lösungsansatz mit Hilfsebene
2. Lösungsansatz: Anwenden des Skalarprodukts
3. Lösungsansatz: Anwenden der Differentialrechnung
\[M(-40|30|30), \qquad g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}, \enspace \lambda \in \mathbb R\]
Abstand eines Punktes von einer Geraden
1. Lösungsansatz mit Hilfsebene
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
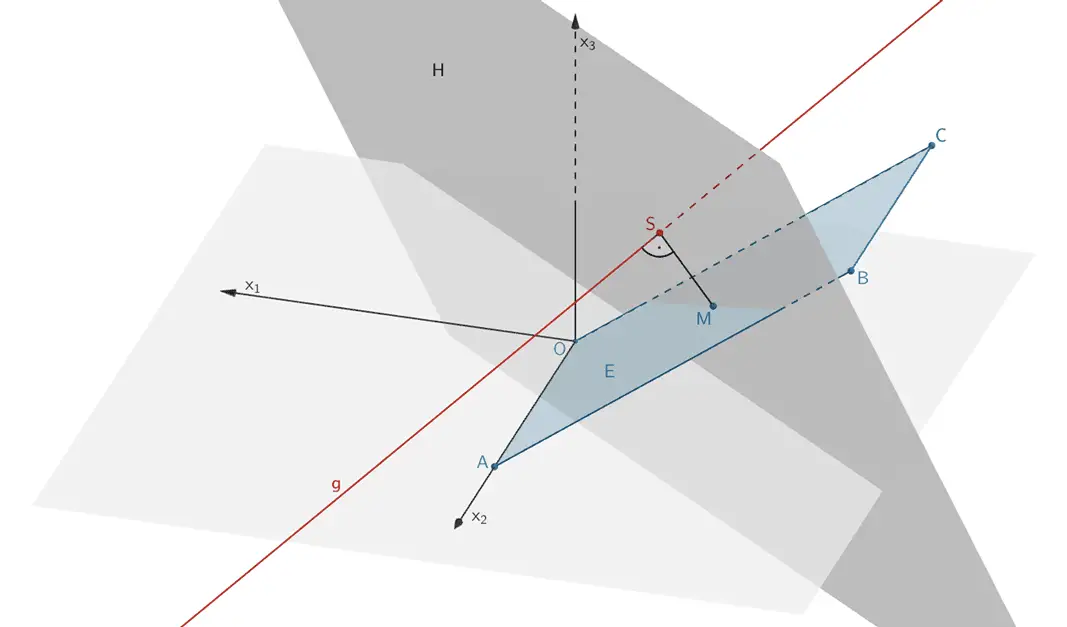
Hilfsebene \(H\) mit den Eigenschaften \(M \in H\) und \(H \perp g\) bestimmen:
\[\overrightarrow {n}_H = \overrightarrow {u}_g = \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}\]
\[H \colon \enspace \overrightarrow {n}_H \circ \left( \overrightarrow X - \overrightarrow M \right) = 0\]
\[H \colon \; \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right] = 0 \]
Lage der Hilfsebene H
Hilfsebene \(\,H\,\) mit den Eigenschaften \(\,M \in H\,\) und \(\,H \perp g\,\)
Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
Zur Berechnung des Schnittpunktes \(S\) setzt man den Ortsvektor \(\overrightarrow X\) aus der Geradengleichung von \(g\) in die Normalengleichung der Hilfsebene \(H\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}\]
\[H \colon \; \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[ \begin {align*} g \cap H \colon \enspace \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \circ \left[ \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right] &= 0 \\[0.8em] \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \circ \left[ \begin {pmatrix} 20 \\ 10 \\ 10 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \right] &= 0 \\[0.8em] 4 \cdot (20 + 4 \lambda) + 5 \cdot (10 + 5 \lambda) - 3 \cdot (10 - 3 \lambda) &= 0 \\[0.8em] 100 + 50 \lambda &= 0 \\[0.8em] 50 \lambda &= -100 \\[0.8em] \lambda &= -2 \end {align*} \]
Parameterwert \(\lambda = -2\) in \(g\) einsetzen:
\[S \in g \colon \enspace \overrightarrow S = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} - 2 \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} = \begin {pmatrix} -28 \\ 30 \\ 46 \end {pmatrix}\]
Länge der Strecke \([MS]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{MS} &= \vert \overrightarrow S - \overrightarrow M \vert \\[0.8em] &= \left| \begin {pmatrix} -28 \\ 30 \\ 46 \end {pmatrix} - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 12 \\ 0 \\ 16 \end {pmatrix} \right| \\[0.8em] &= \sqrt{12^2 + 0^2 + 16^2} \\[0.8em] &= 20 \end{align*}\]
\(\Longrightarrow \quad d(M; g) = 20 = d(g, E)\) (siehe Teilaufgabe d)
2. Lösungsansatz: Anwenden des Skalarprodukts
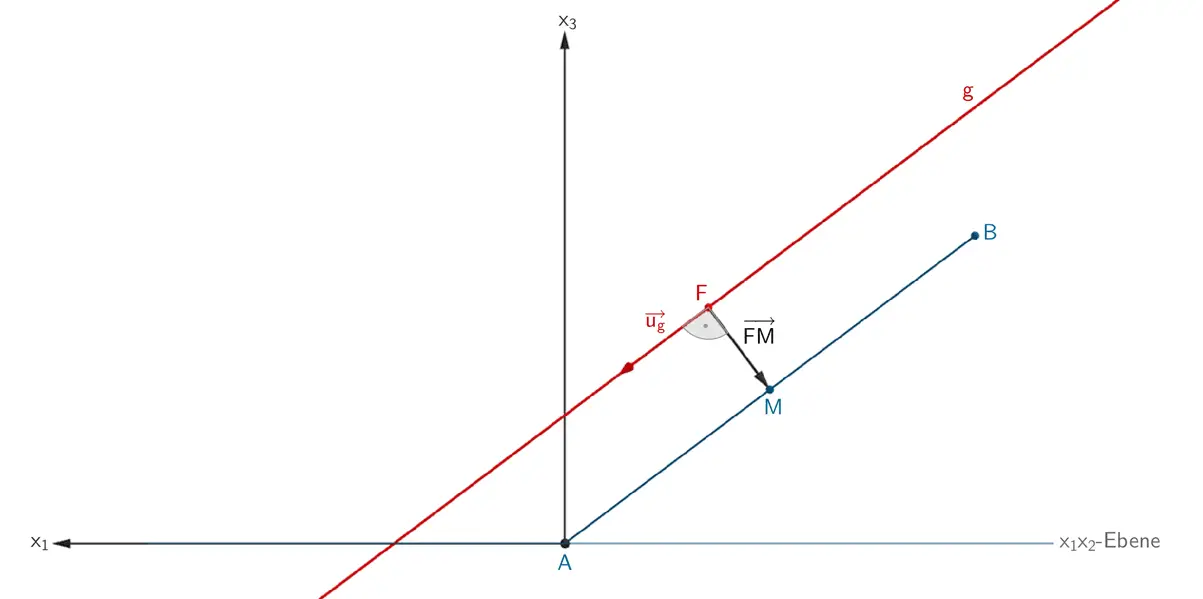
Es sei \(\,F\,\) der Lotfußpunkt des Lotes des Punktes \(\,M\,\) auf die Gerade \(\,g\,\). Der Richtungsvektor \(\,\overrightarrow{u}_g\,\) der Geraden \(\,g\,\) und er Vektor \(\,\overrightarrow{FM}\,\) stehen senkrecht zueinander (\(\,\overrightarrow{u}_g\) schematisch gezeichnet).
\[M(-40|30|30), \qquad g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}, \enspace \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(M\) auf die Gerade \(g\).
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Somit gilt: \(\enspace \overrightarrow{FM} \perp \overrightarrow{u}_g \quad \Longleftrightarrow \quad \overrightarrow{FM} \circ \overrightarrow{u}_g = 0\)
Vektor \(\overrightarrow{FM}\) allgemein beschreiben:
\[F \in g \colon \enspace \overrightarrow F = \begin{pmatrix} -20 + 4 \lambda \\ 40 + 5 \lambda \\ 40 - 3 \lambda \end{pmatrix}\]
\[\begin{align*} \overrightarrow{FM} &= \overrightarrow M - \overrightarrow F \\[0.8em] &= \begin{pmatrix} -40 \\ 30 \\ 30 \end{pmatrix} - \begin{pmatrix} -20 + 4 \lambda \\ 40 + 5 \lambda \\ 40 - 3 \lambda \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -20 - 4 \lambda \\ -10 - 5 \lambda \\ -10 + 3 \lambda \end{pmatrix} \end{align*}\]
Koordinaten des Lotfußpuntes \(F\) bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\overrightarrow{FM} \circ \overrightarrow{u}_g &= 0 \\[0.8em] \begin{pmatrix} -20 - 4 \lambda \\ -10 - 5 \lambda \\ -10 + 3 \lambda \end{pmatrix} \circ \begin{pmatrix} 4 \\ 5 \\ -3 \end{pmatrix} &= 0 \\[0.8em] (-20 - 4 \lambda) \cdot 4 + (-10 - 5 \lambda) \cdot 5 + (-10 + 3 \lambda) \cdot (-3) &= 0 \\[0.8em] -80 - 16 \lambda - 50 - 25 \lambda + 30 - 9 \lambda &= 0 \\[0.8em] -100 - 50 \lambda &= 0 \\[0.8em] -50 \lambda &= 100 \\[0.8em] \lambda &= -2 \end{align*}\]
Parameterwert \(\lambda = -2\) in \(g\) einsetzen:
\[F \in g \colon \enspace \overrightarrow F = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} - 2 \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} = \begin {pmatrix} -28 \\ 30 \\ 46 \end {pmatrix}\]
Länge der Strecke \([MF]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{MF} &= \vert \overrightarrow F - \overrightarrow M \vert \\[0.8em] &= \left| \begin {pmatrix} -28 \\ 30 \\ 46 \end {pmatrix} - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 12 \\ 0 \\ 16 \end {pmatrix} \right| \\[0.8em] &= \sqrt{12^2 + 0^2 + 16^2} \\[0.8em] &= 20 \end{align*}\]
\[\Longrightarrow \quad d(M; g) = 20\]
3. Lösungsansatz: Anwenden der Differentialrechnung
\[M(-40|30|30), \qquad g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}, \enspace \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Differentialrechnung anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Länge der Strecke \([PX]\) zwischen dem Punkt \(P\) und einem beliebigen Punkt \(X \in g\) beschreiben:
\[\overline{PX} = \vert \overrightarrow X - \overrightarrow P \vert \quad \Longrightarrow \quad \overline{PX}(\lambda) = \vert \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \vert\]
2. Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\[\left. \begin{align*} &\overline{PX}^{\;\prime}(\lambda_{min}) \enspace = \enspace 0 \\ \\ &\overline{PX}^{\;\prime \prime}(\lambda_{min}) \; > \enspace 0 \end{align*} \right\} \quad \Longrightarrow \quad \lambda_{min} \]
3. Minimale Länge berechnen:
\[\overline{PX}(\lambda_{min}) = d\,(P;g)\]
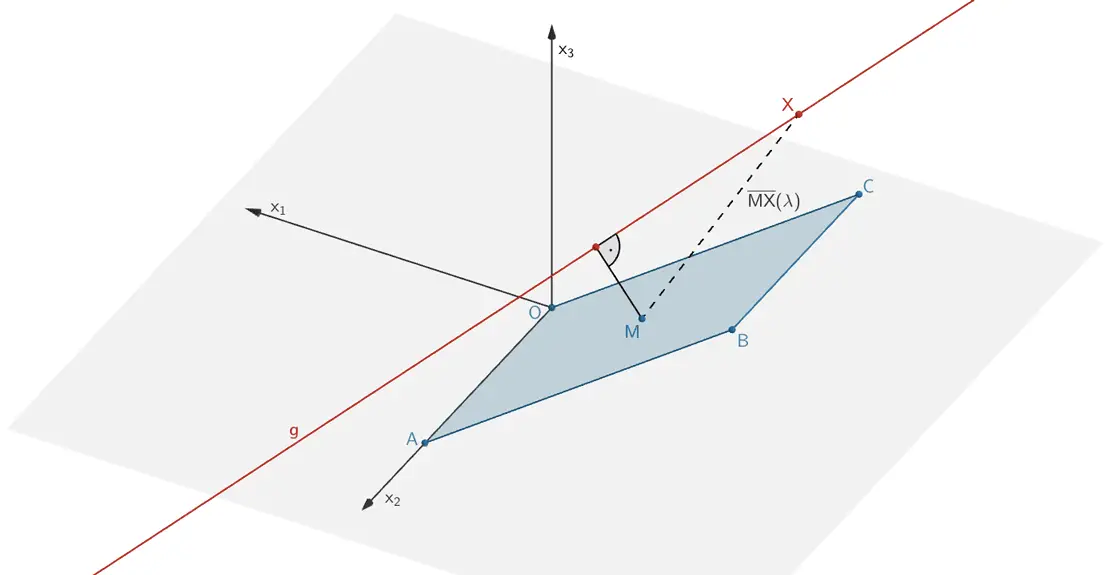
Die Länge der Strecke \(\,[MX]\,\) zwischen dem Punkt \(\,M\,\) und einem beliebigen Punkt \(\,X \in g\,\) lässt sich in Abhängigkeit des Parametrewertes \(\,\lambda\,\) der Geradengleichung von \(\,g\,\) beschreiben.
Länge der Strecke \([MX]\) in Abhängigkeit von \(\lambda\,\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{MX} = \vert \overrightarrow X - \overrightarrow M \vert\]
\[\begin{align*} \overline{MX}(\lambda) &= \left| \begin {pmatrix} -20 + 4\lambda \\ 40 + 5\lambda \\ 40 - 3\lambda \end {pmatrix} - \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 20 + 4\lambda \\ 10 + 5\lambda \\ 10 - 3\lambda \end {pmatrix} \right| \\[0.8em] &= \sqrt{(20 + 4\lambda)^2 + (10 + 5\lambda)^2 + (10 - 3\lambda)^2} \\[0.8em] &= \sqrt{400 + 160\lambda + 16\lambda^2 + 100 + 100\lambda + 25\lambda^2 + 100 - 60\lambda + 9\lambda^2} \\[0.8em] &= \sqrt{50\lambda^2 + 200\lambda + 600} \\[0.8em] &= \sqrt{50(\lambda^2 + 4\lambda + 12)} \end {align*}\]
Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\(\overline{MX}(\lambda)\) ist minimal, wenn der Wert des Radikanden minimal ist.
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[\left [ 50(\lambda^2 + 4\lambda + 12) \right ]' \enspace \overset{!}{=} \enspace 0\]
Erste Ableitung des Radikanden bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\left [ 50(\lambda^2 + 4\lambda + 12) \right ]' = 50(2\lambda + 4)\]
\[\begin{align*} \Longrightarrow \quad 2\lambda + 4 &= 0 \\[0.8em] \lambda &= -2 \end{align*}\]
Art der Extremstelle:
\[\left [ 50(\lambda^2 + 4\lambda + 12) \right ]'' = \left[ 50(2 \lambda + 4) \right]' = 100\]
\[\Longrightarrow \quad \left [ 50(\lambda^2 + 4\lambda + 12) \right ]'' > 0\]
\(\Longrightarrow \quad \overline{MX}(\lambda)\) ist für \(\lambda_{min} = -2\) minimal.
Minimale Länge berechnen:
\[d\,(M;g) = \overline{MX}(\lambda_{min}) = \sqrt{50\left( (-2)^2 + 4 \cdot (-2) +12 \right)} = 20\]