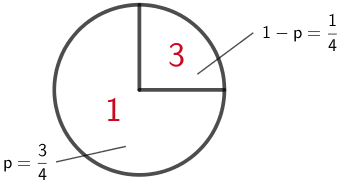
Die Zufallsgröße \(X\) beschreibt die Summe der beiden erzielten Zahlen. Bestimmen Sie, für welchen Wert von \(p\) die Zufallsgröße \(X\) den Erwartungswert 3 hat.
(4 BE)
Lösung zu Teilaufgabe b
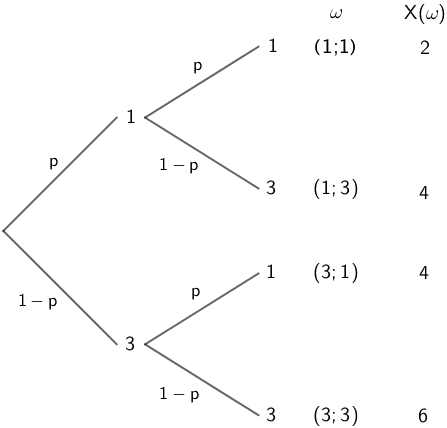
Veranschaulichung mithilfe eines Baumdiagramms. Das Glücksrad wird zweimal gedreht. Die Zufallsgröße \(X\) beschreibt die Summe der beiden erzielten Zahlen.
In Abhängigkeit von \(p\) ergibt sich folgende Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\):
| \(X = x_{i}\) | \(2\) | \(4\) | \(6\) |
| \(P(X = x_{i})\) | \(p^{2}\) | \(2p \cdot (1 - p)\) | \((1 - p)^{2}\) |
(\(P(X = 4) = 2p \cdot (1 - p)\); vgl. Teilaufgabe a)
Der Erwartungswert \(E(X)\) der Zufallsgröße \(X\) soll den Wert 3 annehmen.
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*} E(X) &= 3 \\[0.8em] 2 \cdot p^{2} + 4 \cdot 2p \cdot (1 - p) + 6 \cdot \underbrace{(1 - p)^{2}}_{(a\,-\,b)^{2}} &= 3 &&| \; \text{2. Binom. Formel} \\[0.8em] 2p^{2} + 8p - 8p^{2} + 6 \cdot (\underbrace{1 - 2p + p^{2}}_{a^{2}\,-\,2ab\,+\,b^{2}}) &= 3 \\[0.8em] 2p^{2} + 8p - 8p^{2} + 6 - 12p + 6p^{2} &= 3 \\[0.8em] -4p + 6 &= 3 &&| - 6 \\[0.8em] -4p &= -3 &&| : (-4) \\[0.8em] p &= \frac{3}{4} \end{align*}\]
Anmerkung:
Mit \(p = \frac{3}{4}\) hat der Sektor des Glücksrads mit der Zahl 1 einen Mittelpunktswinkel von 270° (Dreiviertelkreis) und der Sektor mit der Zahl 3 einen Mittelpunktswinkel von 90° (Viertelkreis).