- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{e^x}{e^x - 2}\) mit maximalem Definitionsbereich \(D\).
Bestimmen Sie \(D\) und geben Sie die Koordinaten des Schnittpunkts des Graphen von \(f\) mit der \(y\)-Achse an.
(3 BE)
- Details
- Kategorie: Analysis 2
Geben Sie einen Term der ersten Ableitungsfunktion von \(f\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R_0^+\) definierte Funktion \(g \colon x \mapsto \sqrt{x} + 1\).
Bestimmen Sie eine Gleichung der Tangente an den Graphen von \(g\) im Punkt \((1|g(1))\).
(3 BE)
- Details
- Kategorie: Analysis 2
Die Funktion \(g\) ist umkehrbar. Die Umkehrfunktion \(g^{-1}\) von \(g\) ist in \([1;+\infty[\) definiert. Bestimmen Sie einen Term von \(g^{-1}\).
(2 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto -x^2 + 2ax\) mit \(a \in \; ]1;+\infty[\). Die Nullstellen von \(f\) sind \(0\) und \(2a\).
Zeigen Sie, dass das Flächenstück, das der Graph von \(f\) mit der \(x\)-Achse einschließt, den Inhalt \(\frac{4}{3}a^3\) hat.
(2 BE)
- Details
- Kategorie: Analysis 2
Der Hochpunkt des Graphen von \(f\) liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung 1). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von \(f\) mit der \(x\)-Achse einschließt, überein. Bestimmen Sie den Wert von \(a\).
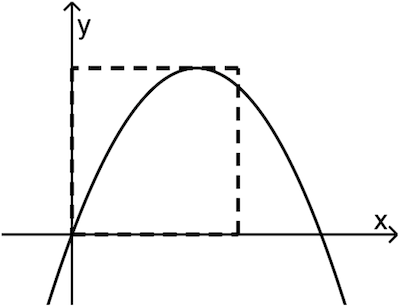Abb. 1
(3 BE)
- Details
- Kategorie: Analysis 2
Abbildung 2 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(g\), dessen einzige Extrempunkte \((-1|1)\) und \((0|0)\) sind, sowie den Punkt \(P\).
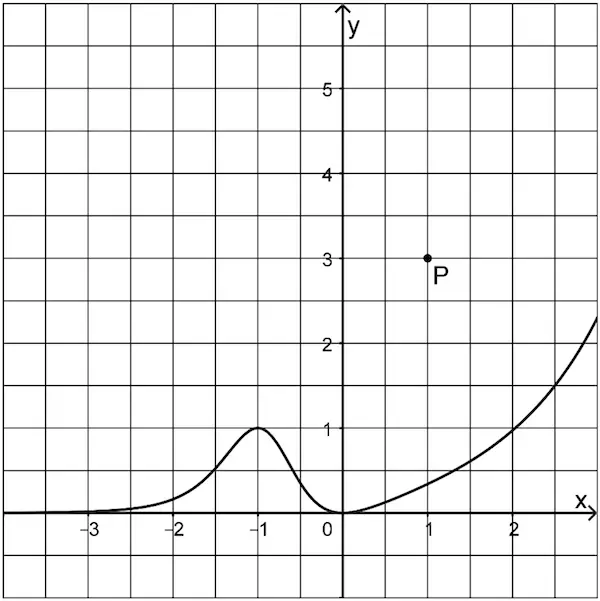Abb. 2
Geben Sie die Koordinaten des Tiefpunkts des Graphen der in \(\mathbb R\) definierten Funktion \(h(x) = -g(x - 3)\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Der Graph einer Stammfunktion von \(g\) verläuft durch \(P\). Skizzieren Sie diesen Graphen in Abbildung 2.
(3 BE)
