Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein \(t \in [0;10]\) die Beziehung \(V(t + 6) = V(t) - 350\) gilt. Entscheiden Sie mithilfe von Abbildung 2, ob für \(t = 5\) diese Beziehung gilt, und begründen Sie Ihre Entscheidung.

(3 BE)

Lösung zu Teilaufgabe 2c

Mathematische Beziehung im Sachzusammenhang interpretieren

Erläuterung der Beziehung \(V(t + 6) = V(t) - 350\) im Sachzusammenhang

\[V(t + 6) = V(t) - 350; \; t \in [0;10]\]

Bedeutung der Terme der Beziehung:

\(V(t)\): Wasservolumen zu einem betrachteten Zeitpunkt \(t\)

\(V(t + 6)\): Wasservolumen sechs Stunden nach einem betrachteten Zeitpunkt \(t\)

\(V(t) - 350\): Ein um 350 m³ geringeres Wasservolumen als zum betrachteten Zeitpunkt \(t\)

Bedeutung im Sachzusammenhang:

Sechs Stunden nach einem beliebigen Zeitpunkt \(t \in [0;10]\) beträgt das Wasservolumen um 350 m³ weniger als zum Zeitpunkt \(t\).

Entscheidung, ob für \(t = 5\) die Beziehung \(V(t + 6) = V(t) - 350\) gilt

\[V(t + 6) = V(t) - 350 \enspace \Longleftrightarrow \enspace V(t) - V(t + 6) = 350\]

\[t = 5 \colon V(5) - V(11) = 350\]

Es ist mithilfe von Abbildung 2 zu überprüfen, ob die Gleichung \(V(5) - V(11) = 350\) näherungsweise erfüllt ist.

 

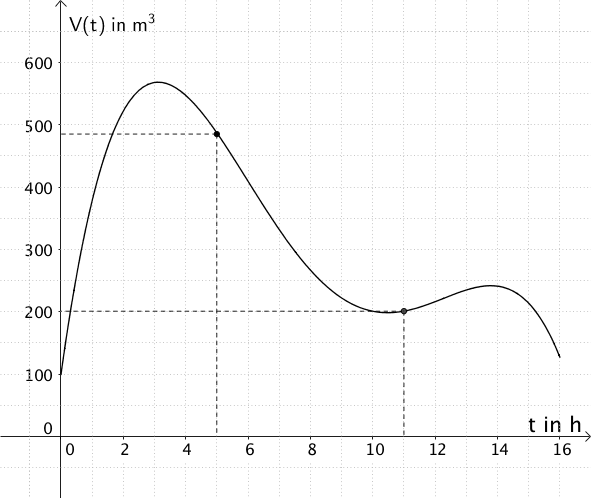
Näherungsweise Bestimmung der Funktionswerte \(V(5)\) und \(V(11)\)

\(V(5) \approx 485\) (vgl. Teilaufgabe 2a)

\[V(11) \approx 200\]

\[V(5) - V(11) = 485 - 200 = 285 \neq 350\]

Entscheidung:

Die Beziehung \(V(t + 6) = V(t) - 350\) gilt nicht für \(t = 5\).