Aufgabe 1
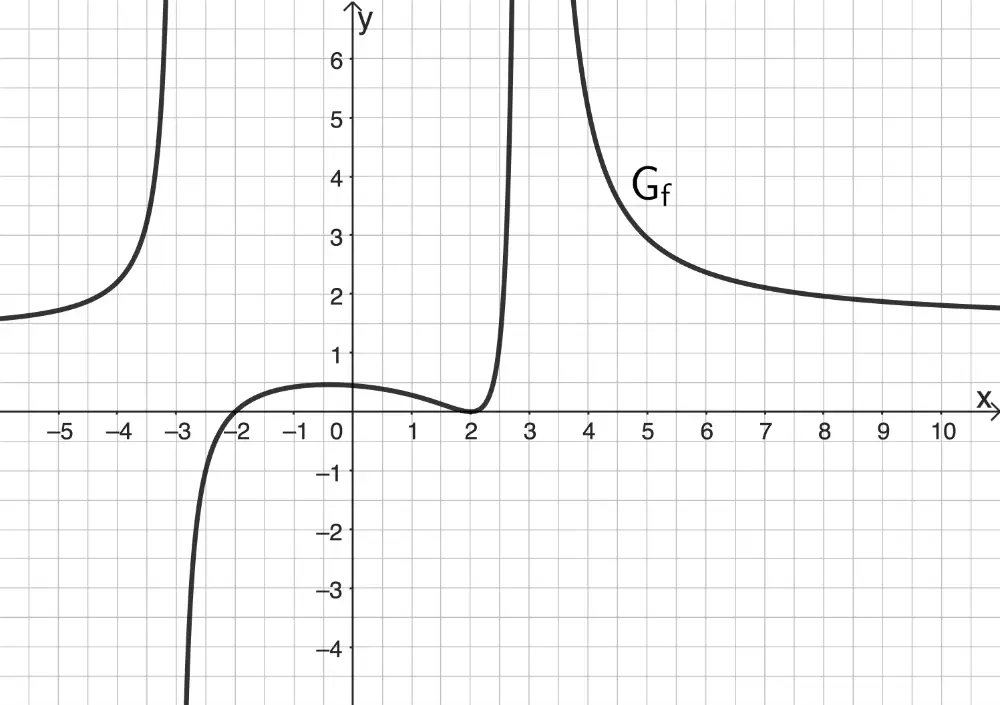
Die Abbildung zeigt den Graphen \(G_f\) der gebrochenrationalen Funktion \(f\).
Geben Sie in Stichpunkten alle Eigenschaften der Funktion \(f\) an, die Sie dem Graphen \(G_f\) entnehmen können und bestimmen Sie damit einen möglichst einfachen Funktionsterm der Funktion \(f\).
Aufgabe 2
Beurteilen Sie folgende Aussage:
Der Graph einer gebrochenrationalen Funktion, bei der das Zähler- und das Nennerpolynom jeweils höchstens Grad 2 aufweist, kann mit einer Gerade maximal drei gemeinsame Punkte haben.
Aufgabe 3
Die Wirksamkeit eines Medikaments wird an Probanden getestet, die entweder das Medikament oder ein Placebo verabreicht bekommen.
Betrachtet werden folgende Ereignisse:
\(M\): „Der Proband nimmt das Medikament ein."
\(G\): „Der Proband wird gesund."
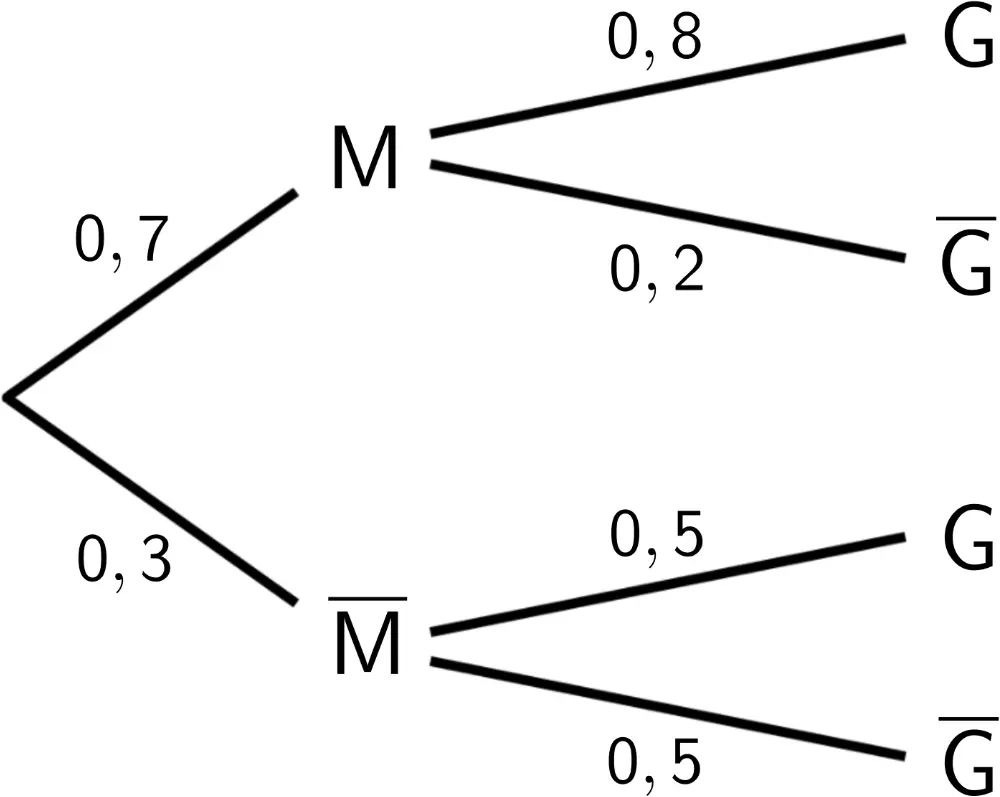
Das Baumdiagramm informiert darüber, mit welcher Wahrscheinlichkeit die Ereignisse jeweils eintreten.
- Beschreiben Sie die Bedeutung des Werts \(0{,}8\) im Sachzusammenhang in Worten.
- Stellen Sie den Sachverhalt mit Hilfe einer vollständig ausgefüllten Vierfeldertafel dar.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass ein Proband, der gesund wurde, ein Placebo verabreicht bekam.
Aufgabe 4
Betrachtet werden die stochastisch unabhängigen Ereignisse \(A\) und \(B\) und es gilt: \(P(A \cap B) = 0{,}4\). Entscheiden Sie, welche der folgenden Aussagen sicher richtig, sicher falsch oder anhand der vorliegenden Informationen nicht eindeutig sind. Begründen Sie jeweils Ihre Entscheidung.
\[\textsf{(1)}\quad P(B) = 0{,}6\]
\[\textsf{(2)}\quad P_A(B) = P(B)\]
\[\textsf{(3)}\quad P(A) \cdot P(B) = 0{,}5\]
Aufgabe 5
Gegeben ist die in \(\mathbb R\) definierte Funktion \(g\) mit \(g(x) = \frac{3}{4}x^2 + x\).
Bestimmen Sie mit Hilfe des Differentialquotienten die Steigung des Graphen von \(g\) an der Stelle \(x_0 = -2\). Verwenden Sie die \(\boldsymbol{h}\)-Methode.
Aufgabe 6
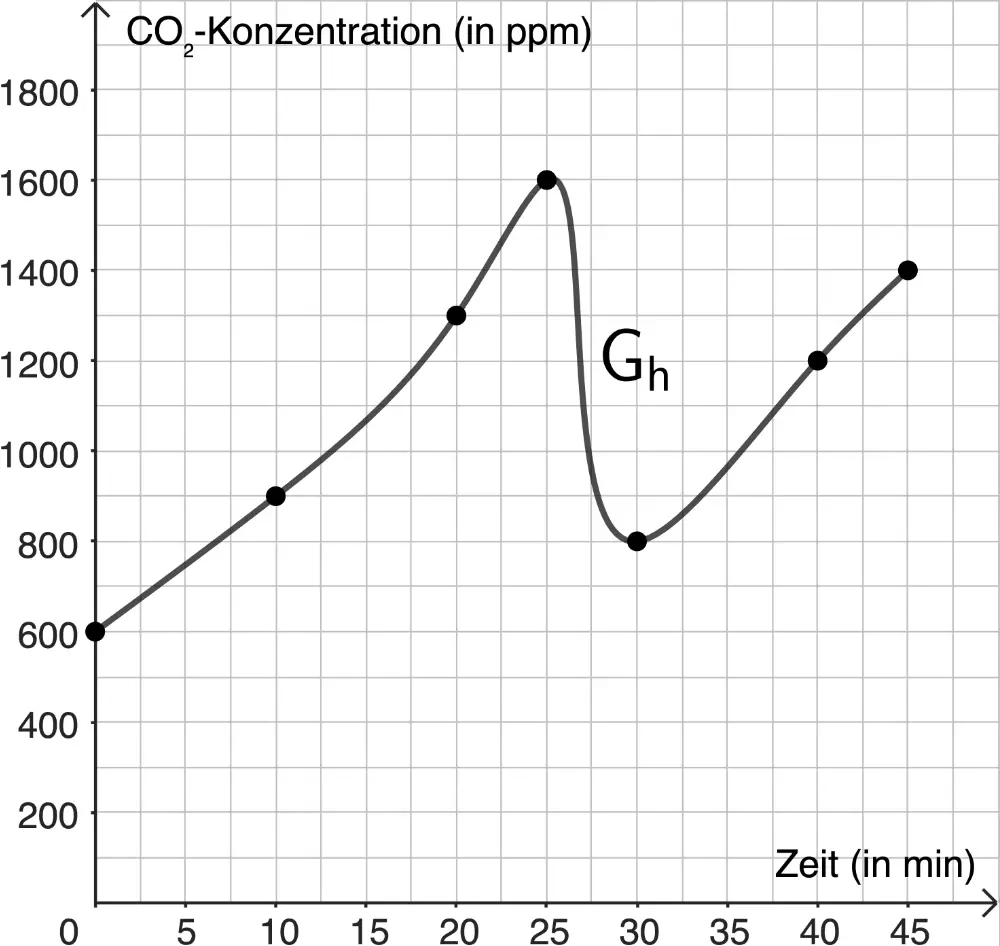
Die Abbildung zeigt einige Messwerte der Überwachung der CO₂-Konzentration während einer Unterrichtsstunde in einem Schulungsraum. Der Graph \(G_h\) der Funktion \(h\) beschreibt annähernd den Verlauf aller Messwerte.
- Bestimmen Sie mit Hilfe der Abbildung \(\dfrac{h(20) - h(10)}{20-10}\), \(h(25)\) und \(h'(27{,}5)\). Veranschaulichen Sie Ihre Vorgehensweise jeweils in der Abbildung. Interpretieren Sie jedes der drei Ergebnisse im Sachzusammenhang.
- Ermitteln Sie näherungsweise den Zeitpunkt \(t_1\), an dem die CO₂-Konzentration am schnellsten zunimmt. Beschreiben Sie Ihre Vorgehensweise kurz in einem Satz.
- Geben Sie einen Wert für den Zeitpunkt \(t_2\) an, an dem \(h'(t_2) = 0\) gilt.


