Vor allem in Naturwissenschaft und Technik treten Größen auf, welche sich nur durch die Angabe der Richtung der Größe vollständig formulieren lassen. Während ein Skalar eine Größe ist, die sich eindeutig durch die Angabe einer Maßzahl und einer Maßeinheit beschreiben lässt, benötigt eine vektorielle Größe zusätzlich die Angabe der Richtung, in die sie wirkt.
Beispiele:
Skalare: Masse \(m\), Temperatur \(T\), Zeit \(t\)
Vektoren: Geschwindigkeit \(\overrightarrow{v}\), Beschleunigung \(\overrightarrow{a}\), Kraft \(\overrightarrow{F}\)
Ein Vektor \(\overrightarrow{a}\) ist durch seine Länge und seine Richtung festgelegt. Anschaulich beschreibt ein Vektor die Menge aller gleich langer und gleichgerichteter Pfeile. Jeder einzelne Pfeil heißt Repräsentant.
Spezielle Vektoren und Bezeichnungen
Die nachfolgenden Beschreibungen beziehen sich auf Vektoren im Raum. Sie gelten analog für Vektoren in der Ebene.
Schreibweise als Spaltenvektor
\(\overrightarrow{a} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix}\)
Die reellen Zahlen \(a_{1}, a_{2}\) und \(a_{3}\) heißen Vektorkoordinaten.
Nullvektor
Ein Vektor vom Betrag Null (mit der Länge Null) heißt Nullvektor (vgl. Betrag eines Vektors).
\[\overrightarrow{0} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\]
Gegenvektor
Der zu einem Vektor \(\overrightarrow{a}\) gehörende Gegenvektor \(-\overrightarrow{a}\) hat die gleiche Länge wie der Vektor \(\overrightarrow{a}\), jedoch die entgegengesetzte Richtung.
Verbindungsvektor
Der Vektor, der den Punkt \(P(p_{1}|p_{2}|p_{3})\) zu dem Punkt \(Q(q_{1}|q_{2}|q_{3})\) verschiebt, wird als Verbindungsvektor \(\overrightarrow{PQ}\) bezeichnet.
\[\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P}\]
(vgl. Subtraktion von Vektoren)
Ortsvektor
Ein Ortsvektor führt vom Koordiantenursprung \(O\) zu einem Punkt \(P\).
\[\overrightarrow{OP} = \overrightarrow{P} = \begin{pmatrix} p_{1} \\ p_{2} \\ p_{3} \end{pmatrix}\]
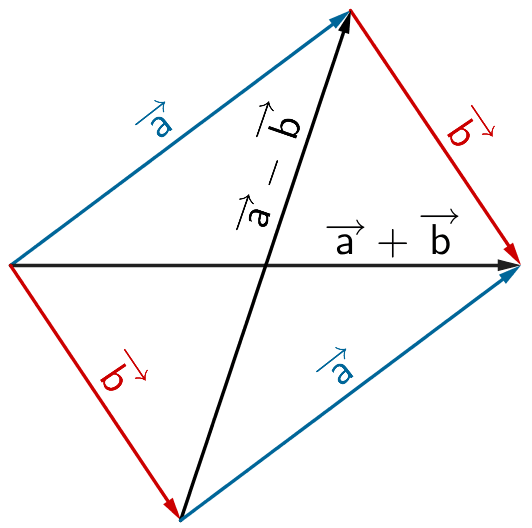
Addition und Subtraktion von Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) werden koordinatenweise addiert bzw. subtrahiert. Die Addition des Gegenvektors \(-\overrightarrow{b}\) zu dem Vektor \(\overrightarrow{a}\) bezzeichnet man als Subtraktion von Vektoren: \(\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + (-\overrightarrow{b})\)
Addition und Subtraktion von Vektoren
\[\overrightarrow{a} + \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} + \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = \begin{pmatrix} a_{1} + b_{1} \\ a_{2} + b_{2} \\ a_{3} + b_{3} \end{pmatrix}\]
\[\overrightarrow{a} - \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} - \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = \begin{pmatrix} a_{1} - b_{1} \\ a_{2} - b_{2} \\ a_{3} - b_{3} \end{pmatrix}\]
Multiplikation eines Vektors mit einem Skalar
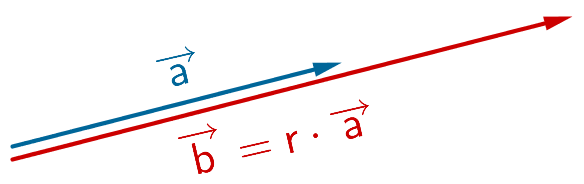
Bei der Multiplikation eines Vektors \(\overrightarrow{a}\) mit einer reellen Zahl \(r\) (Skalar) wird jede Koordinate des Vektors mit \(r\) multipliziert. Es entsteht ein neuer Vektor \(\overrightarrow{b} = r \cdot \overrightarrow{a}\), dessen Betrag das \(\vert r \vert\)-fache des Betrages von \(\overrightarrow{a}\) ist (vgl. Betrag eines Vektors).
Für \(r > 0\) sind die Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) gleichgerichtet. Für \(r < 0\) sind die Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) entgegengesetzt gerichtet. Für den Spezialfall \(r = -1\) entsteht der Gegenvektor \(\overrightarrow{b} = -\overrightarrow{a}\).
Skalare Multiplikation
\[\overrightarrow{b} = r \cdot \overrightarrow{a} = r \cdot \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} = \begin{pmatrix}r \cdot a_{1} \\ r \cdot a_{2} \\ r \cdot a_{3} \end{pmatrix}\]
\(r > 0 \colon \; \overrightarrow{a}, \overrightarrow{b}\) gleichgerichtet
\(r < 0 \colon \; \overrightarrow{a}, \overrightarrow{b}\) entgegengesetzt gerichtet
\(r = -1 \colon \; \overrightarrow{b} = -\overrightarrow{a}\) (Gegenvektor)
\[\vert \overrightarrow{b} \vert = \vert r \vert \cdot \vert \overrightarrow{a} \vert\]
Betrag eines Vektors und Einheitsvektor
Der Betrag eines Vektors gibt die Länge eines Vektors an. Jeder Vektor vom Betrag Eins wir als Einheitsvektor bezeichnet. Mit \(\overrightarrow{a}^{0}\) oder \(\overrightarrow{a_{0}}\) bezeichnet man den zu \(\overrightarrow{a}\) gehörenden Einheitsvektor (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
Betrag eines Vektors und Einheitsvektor
\[\vert \overrightarrow{a} \vert = \sqrt{a^{2}_{1} + a^{2}_{2} + a^{2}_{3}} \qquad \quad \overrightarrow{a}^{0} = \dfrac{\overrightarrow{a}}{\vert \overrightarrow{a}\vert}\]
Anwendungen der Vektorrechnung
Mithilfe der Vektorrechnung kann beispielweise die Länge einer Strecke \([AB]\), der Mittelpunkt einer Strecke \([AB]\) oder der Schwerpunkt eines Dreiecks berechnet werden.
Länge einer Strecke \(\boldsymbol{[AB]}\)
\[\overline{AB} = \vert \overrightarrow{AB} \vert = \sqrt{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2} + (b_{3} - a_{3})^{2}}\]
Mittelpunkt einer Strecke \(\boldsymbol{[AB]}\) (vgl. Merkhilfe)
Für den Ortsvektor des Mittelpunkts \(M\) der Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \cdot \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
Schwerpunkt eines Dreiecks \(\boldsymbol{ABC}\) (vgl. Merkhilfe)
Für den Ortsvektor des Schwerpunkts \(S\) des Dreiecks \(ABC\) gilt:
\[\overrightarrow{S} = \frac{1}{3} \cdot \left( \overrightarrow{A} + \overrightarrow{B} + \overrightarrow{C} \right)\]
Beispielaufgabe
Gegeben seien die Punkte \(A(4|1|2)\), \(B(6|7|3)\), \(C(-3|3|8)\) und \(D(-5|-3|7)\).
Weisen Sie nach, dass das Viereck \(ABCD\) ein Parallelogramm ist. Bestimmen Sie die Koordinaten des Punktes \(P\), der vom Punkt \(D\) in Richtung des Vektors \(\overrightarrow{v} = \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix}\) um 12 Längeneinheiten entfernt liegt.
Nachweis, dass das Viereck \(ABCD\) ein Parallelogramm ist
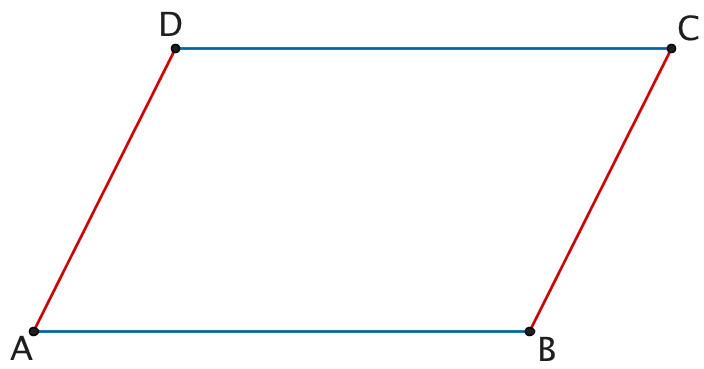
Planskizze: Parallelogramm \(ABCD\)
Das Viereck \(ABCD\) ist ein Parallelogramm, wenn je zwei gegenüberliegende Seiten parallel zueinander und gleich lang sind (die Sonderfälle Rechteck und Quadrat mit eingeschlossen).
\[[AB] \parallel [DC]\,; \enspace [BC] \parallel [AD]\]
und
\[\overline{AB} = \overline{DC}\,; \enspace \overline{BC} = \overline{AD}\]
Verbindungsvektoren \(\overrightarrow{AB}\), \(\overrightarrow{DC}\), \(\overrightarrow{BC}\) und \(\overrightarrow{AD}\) berechnen:
\[A(4|1|2), \enspace B(6|7|3), \enspace C(-3|3|8), \enspace D(-5|-3|7)\]
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 6 \\ 7 \\ 3 \end{pmatrix} - \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix}\]
\[\overrightarrow{DC} = \overrightarrow{C} - \overrightarrow{D} = \begin{pmatrix} -3 \\ 3 \\ 8 \end{pmatrix} - \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} = \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix}\]
\[\overrightarrow{BC} = \overrightarrow{C} - \overrightarrow{B} = \begin{pmatrix} -3 \\ 3 \\ 8 \end{pmatrix} - \begin{pmatrix} 6 \\ 7 \\ 3 \end{pmatrix} = \begin{pmatrix} -9 \\ -4 \\ 5 \end{pmatrix}\]
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} - \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -9 \\ -4 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{AB} \parallel \overrightarrow{DC} \quad \Longrightarrow \quad [AB] \parallel [DC]\]
\[\Longrightarrow \quad \overrightarrow{BC} \parallel \overrightarrow{AD} \quad \Longrightarrow \quad [BC] \parallel [AD]\]
\[\Longrightarrow \quad \overline{AB} = \vert \overrightarrow{AB} \vert = \vert \overrightarrow{DC} \vert = \overline{DC}\]
\[\Longrightarrow \quad \overline{BC} = \vert \overrightarrow{BC} \vert = \vert \overrightarrow{AD} \vert = \overline{AD}\]
\(\Longrightarrow \quad\)Das Viereck \(ABCD\) ist ein Parallelogramm.
Koordinaten des Punktes \(P\)
\[D(-5|-3|7), \; \overrightarrow{v} = \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix}; \; d(P;D) = 12\]
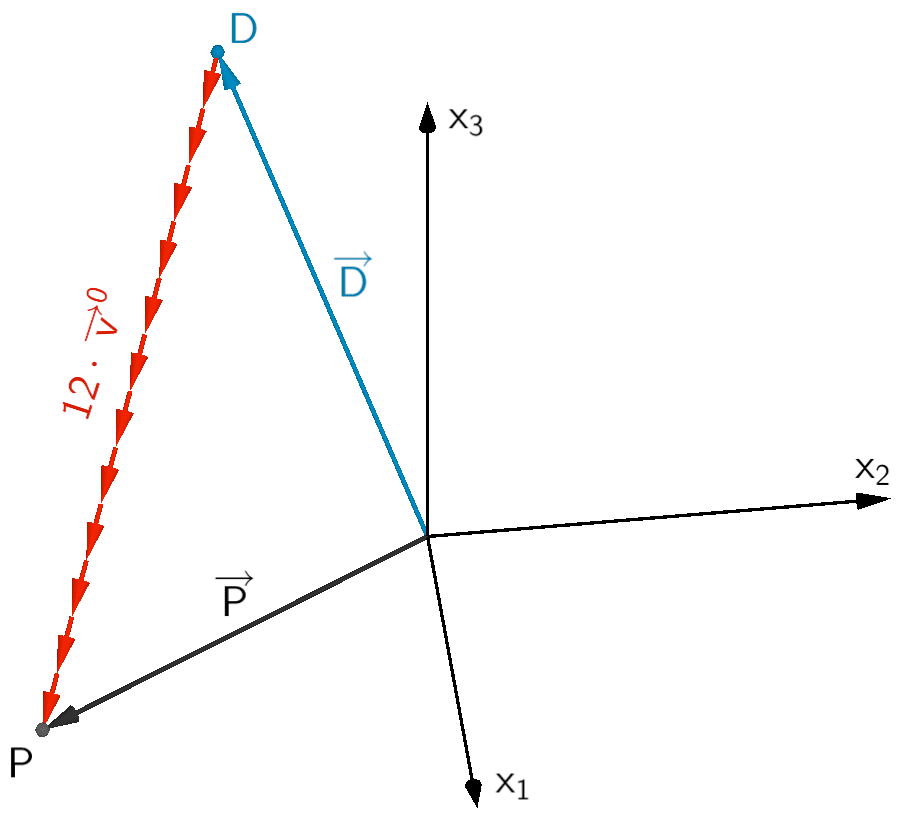
Man erhält den Ortsvektor \(\overrightarrow{P}\), indem man zum Ortsvektor \(\overrightarrow{D}\) das zwölffache des Einheitsvektors \(\overrightarrow{v}^{0}\) des Vektors \(\overrightarrow{v}\) addiert.
\[\overrightarrow{P} = \overrightarrow{D} + 12 \cdot \overrightarrow{v}^{0}\]
Einheitsvektor \(\overrightarrow{v}^{0}\) berechnen:
\[\overrightarrow{v}^{0} = \frac{\overrightarrow{v}}{\vert \overrightarrow{v} \vert} = \frac{\begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix}}{\left| \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix} \right|} = \frac{\begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix}}{\sqrt{4^{2} + (-2)^{2} + (-4)^{2}}} = \frac{1}{6} \cdot \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix}\]
Koordinaten des Punktes \(P\) ermitteln:
\[\begin{align*} \overrightarrow{P} &= \overrightarrow{D} + 12 \cdot \overrightarrow{v}^{0} \\[0.8em] &= \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + 12 \cdot \frac{1}{6} \cdot \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + \begin{pmatrix} 8 \\ -4 \\ -8 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3 \\ -7 \\ -1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad P(3|-7|-1)\]


