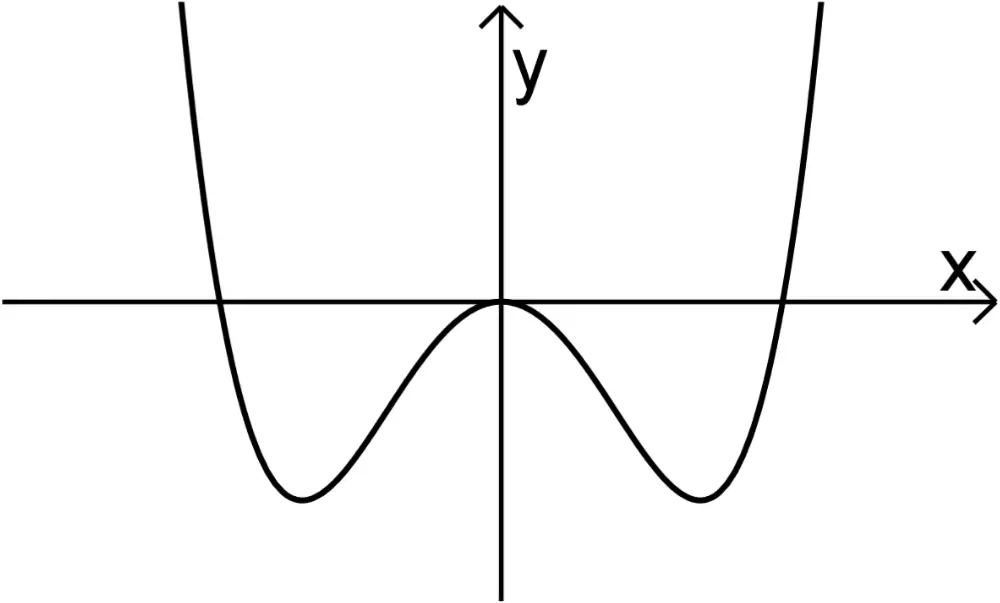
Gegeben ist eine in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = x^4 - kx^2\), wobei \(k\) eine positive reelle Zahl ist. Die Abbildung zeigt den Graphen von \(f\).
- Zeigen Sie, dass \(f'(x) = 2x \cdot \left( 2x^2-k \right)\) ein Term der ersten Ableitungsfunktion von \(f\) ist.
(1 BE) - Die beiden Tiefpunkte des Graphen von \(f\) haben jeweils die \(y\)-Koordinate \(-1\). Ermitteln Sie den Wert von \(k\).
(4 BE)
Lösung zu Aufgabe A2
\[f(x) =x^4 - kx^2; \; D_f = \mathbb R,\; k > 0\]
a) Nachweis des Terms \(f'(x) = 2x \cdot \left( 2x^2-k \right)\)
\[f(x) =x^4 - \textcolor{#e9b509}{k}x^2\]
Beim Ableiten wird auf den Parameter \(\textcolor{#e9b509}{k}\) die Faktorregel angewendet.
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f'(x) = 4x^3 - \textcolor{#e9b509}{k} \cdot 2x = 2x \cdot \left( 2x^2 - \textcolor{#e9b509}{k}\right)\]
b) Wert des Parameters \(k\)
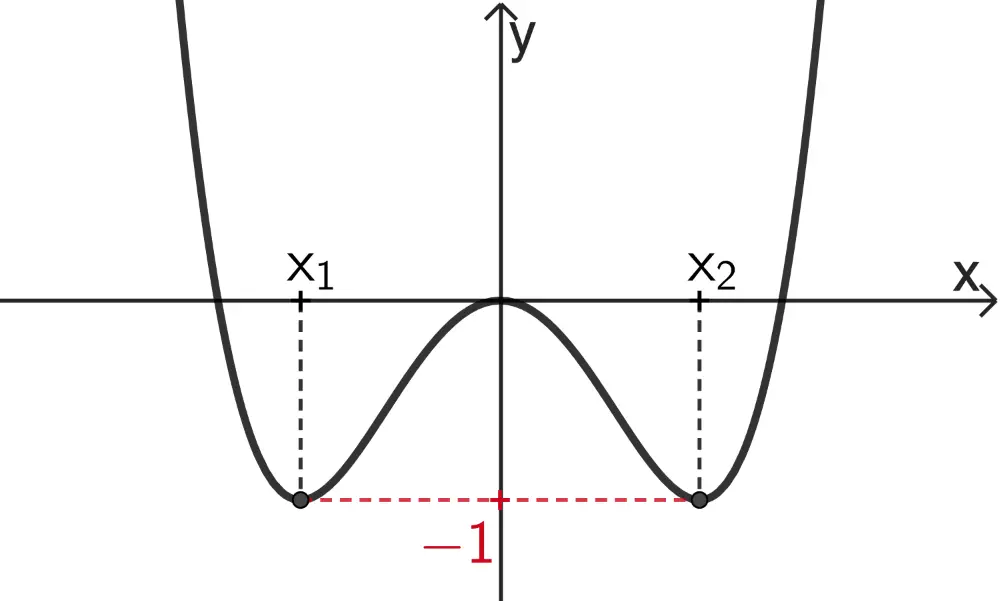
Es seien \((x_1|\textcolor{#cc071e}{-1})\) und \((x_2|\textcolor{#cc071e}{-1})\) die beiden Tiefpunkte des Graphen von \(f\) mit der \(\textcolor{#cc071e}{y}\)-Koordinate \(\textcolor{#cc071e}{-1}\).
\[f(x_1) = f(x_2) = \textcolor{#cc071e}{-1}\]
Vorgehensweise
1. Extremstelle \(x_1\) bzw. \(x_2\) in Abhängigkeit des Parameters \(k\) bestimmen.
2. Für \(f(x_1) = \textcolor{#cc071e}{-1}\) oder \(f(x_2) = \textcolor{#cc071e}{-1}\) den zugehörigen Wert des Parameters \(k\) ermitteln.
Extremstellen von \(\boldsymbol{f}\) in Abhängigkeit des Parameters \(\boldsymbol{k}\) bestimmen
Extremstelle(n) bestimmen
Extremstelle(n) bestimmen mit Vorzeichenwechsel der 1. Ableitung
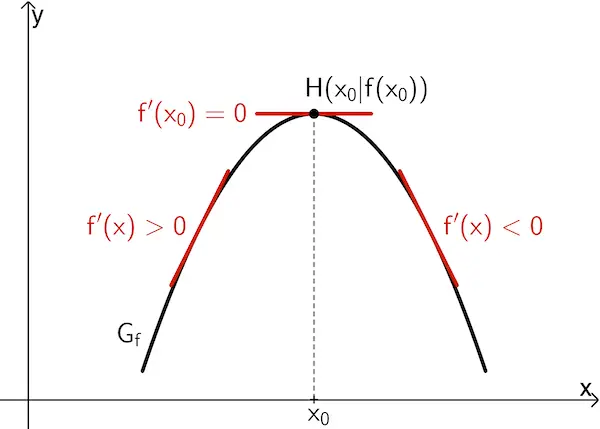
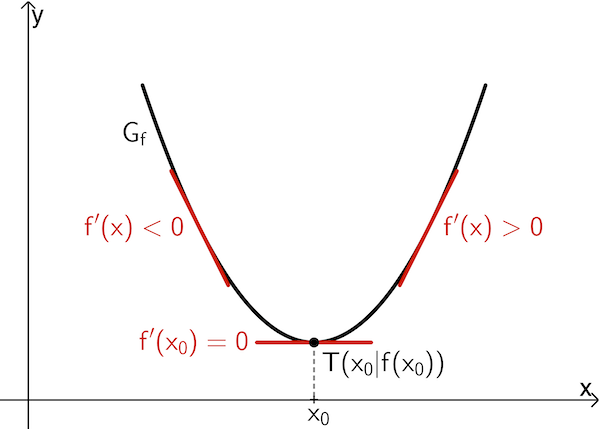
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#cc071e}{f'(x_0) = 0}\) ist und \(\textcolor{#cc071e}{f'}\) bei \(x_0\) einen Vorzeichenwechsel
von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{–}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#cc071e}{+}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
Extremstelle(n) bestimmen mit Vorzeichen der 2. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
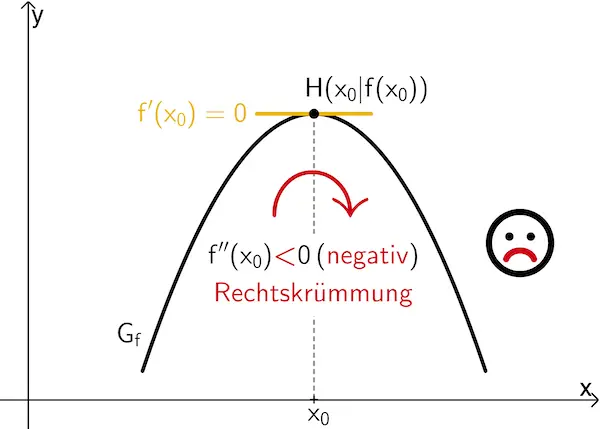
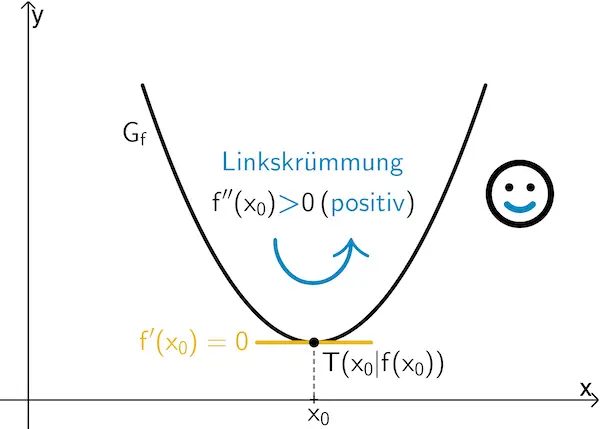
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
\[\begin{align*}f'_k(x) &=0 \\ 2x \cdot \left( 2x^2 - k \right) &= 0 \end{align*}\]
Für die \(x\)-Koordinaten der beiden Tiefpunkte gilt \(x \neq 0\) (vgl. Abbildung).
Somit folgt:
\[\begin{align*}2x^2 - k &= 0 &&| + k \\ 2x^2 &= k &&| :2 \\ x^2 &= \frac{k}{2} &&| \; \sqrt{\quad}\; (k > 0) \\ x_{1,2} &= \pm \sqrt{\frac{k}{2}}\end{align*}\]
Da \(x_{1,2} = \pm \sqrt{\frac{k}{2}}\) einfache Nullstellen mit Vorzeichenwechsel von \(f'\) sind, sind diese Extremstellen von \(f\).
Wert des Parameters \(\boldsymbol{k}\) ermitteln
\[\begin{align*} f\Big(\textstyle \sqrt{\frac{k}{2}}\Big) &= -1 \\ \left(\sqrt{\frac{k}{2}}\right)^4 - k \cdot \left(\sqrt{\frac{k}{2}}\right)^2 &= -1 \\ \frac{k^2}{4} - k \cdot \frac{k}{2} &= -1 \\ \frac{k^2}{4} - \frac{k^2}{2} &= -1 \\ -\frac{k^2}{4} &= -1 &&| \cdot (-4) \\ k^2 &= 4 &&| \; \sqrt{\quad} \; (k > 0) \\ k &= 2 \end{align*}\]
Für \(k = 2\) haben die beiden Tiefpunkte des Graphen von \(f\) jeweils die \(y\)-Koordinate -1.
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.4.2 Extremstellen einer Funktionenschar)
