Die drei Urnen mit den in der Abbildung dargestellten Inhalten bilden den Ausgangspunkt für folgendes Spiel:
Es wird zunächst ein Einsatz von 1 € eingezahlt. Anschließend wird eine der drei Urnen zufällig ausgewählt und danach aus dieser Urne eine Kugel zufällig gezogen. Nur dann, wenn diese Kugel schwarz ist, wird ein bestimmter Geldbetrag ausgezahlt.
Ermitteln Sie, wie groß dieser Geldbetrag sein muss, damit bei diesem Spiel auf lange Sicht Einsätze und Auszahlungen ausgeglichen sind.
(3 BE)
Lösung zu Teilaufgabe 2b
Wahrscheinlichkeitsverteilung einer Zufallsgröße, Erwartungswert einer Zufallsgröße
Damit bei dem Spiel auf lange Sicht Einsätze und Auszahlungen ausgeglichen sind, muss der im Mittel zu erwartende Auszahlungsbetrag pro Spiel gleich dem Betrag des pro Spiel eingezahlten Einsatzes sein. Oder es muss der im Mittel zu erwartende Gewinn pro Spiel gleich 0 € sein (faires Spiel).
1. Lösungsansatz: Erwartungswert des Auszahlungsbetrags
Es sei \(X\) die Zufallsgröße, die jedem Ergebnis des Zufallsexperiments einen Auszahlungsbetrag in Euro zuordnet.
Es sei \(a\) der unbekannten Geldbetrag, der ausgezahlt wird, wenn aus einer Urne zufällig eine schwarze Kugel gezogen wird.
Baumdiagramm des Zufallsexperiments:
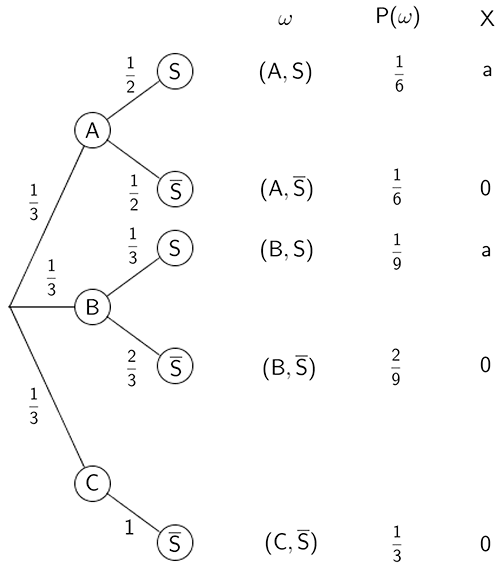
Baumdiagramm des Zufalsexperiments (Spiel) mit Ergebnissen und den zugeordneten Werten der Zufallsgröße \(X\) (Auszahlungsbetrag in Euro)
Die Wahrscheinlichkeit, zufällig eine der drei Urnen A, B oder C auszuwählen beträgt jeweils \(\frac{1}{3}\). Die Wahrscheinlichkeit, zufällig eine schwarze oder eine weiße Kugel aus der gewählten Urne zu ziehen, hängt von der Verteilung der Kugeln in dieser Urne ab (vgl. Abbildung Angabe).
Die Wahrscheinlichkeiten \(P(\omega)\) der Ergebnisse lassen sich mithilfe der 1. Pfadregel bestimmen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(\{A,S\}) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\]
\[P(\{A,\overline{S}\}) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\]
\[P(\{B,S\}) = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}\]
\[P(\{B,\overline{S}\}) = \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{9}\]
\[P(\{C,\overline{S}\}) = \frac{1}{3} \cdot 1 = \frac{1}{3}\]
Unter Anwendung der 2. Pfadregel ergibt sich folgende Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\):
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(X = 0) &= P(\overline{S}) \\[0.8em] &= P(\{A,\overline{S}\}) + P(\{B,\overline{S}\}) + P(\{C,\overline{S}\}) \\[0.8em] &= \frac{1}{6} + \frac{2}{9} + \frac{1}{3} \\[0.8em] &= \frac{3}{18} + \frac{4}{18} + \frac{6}{18} \\[0.8em] &= \frac{13}{18} \end{align*}\]
\[\begin{align*}P(X = a) &= P(S) \\[0.8em] &= P(\{A,S\}) + P(\{B,S\}) \\[0.8em] &= \frac{1}{6} + \frac{1}{9} \\[0.8em] &= \frac{3}{18} + \frac{2}{18} \\[0.8em] &= \frac{5}{18} \end{align*}\]
| \(X = x_{i}\) | \(0\) | \(a\) |
| \(P(X = x_{i})\) | \(\dfrac{13}{18}\) | \(\dfrac{5}{18}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\)
Erwartungswert \(E(X)\) des Auszahlungsbetrags pro Spiel ermitteln:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*}E(X) &= x_{1} \cdot P(X = x_{1}) + x_{2} \cdot P(X = x_{2}) \\[0.8em] &= 0 \cdot \frac{13}{18} + a \cdot \frac{5}{18} \\[0.8em] &= \frac{5}{18}a \end{align*}\]
Der im Mittel zu erwartende Auszahlungsbetrag pro Spiel muss gleich dem Betrag des pro Spiel eingezahlten Einsatzes sein.
Einsatz: 1 € (vgl. Angabe)
\[\begin{align*} E(X) &= 1 \\[0.8em] \frac{5}{18}a &= 1 & &| : \frac{5}{18} \\[0.8em] a &= \frac{18}{5} \\[0.8em] &= 3{,}6 \end{align*}\]
Damit bei dem Spiel auf lange Sicht Einsätze und Auszahlungen ausgeglichen sind, muss der Geldbetrag, der ausgezahlt wird, wenn aus einer Urne eine schwarze Kugel gezogen wird, 3,6 € betragen.
2. Lösungsansatz: Erwartungswert des Gewinns
Es sei \(G\) die Zufallsgröße, die jedem Ergebnis des Zufallsexperiments einen Gewinn in Euro zuordnet.
Es sei \(a\) der unbekannten Geldbetrag, der ausgezahlt wird, wenn aus einer Urne zufällig eine schwarze Kugel gezogen wird.
Baumdiagramm des Zufallsexperiments:
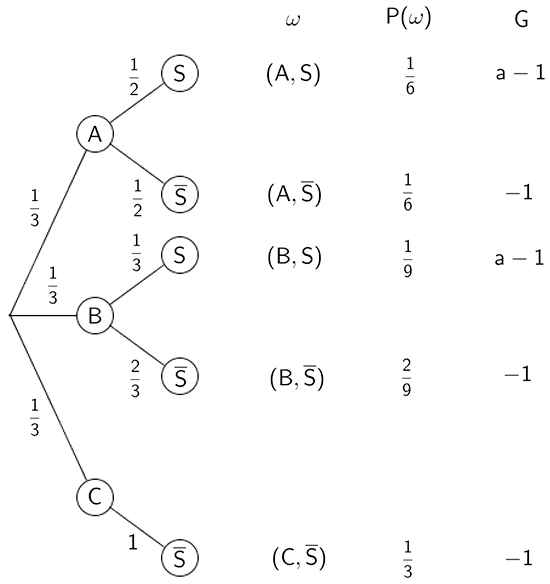
Baumdiagramm des Zufalsexperiments (Spiel) mit Ergebnissen und den zugeordneten Werten der Zufallsgröße \(G\) (Gewinn in Euro)
Die Wahrscheinlichkeit, zufällig eine der drei Urnen A, B oder C auszuwählen beträgt jeweils \(\frac{1}{3}\). Die Wahrscheinlichkeit, zufällig eine schwarze oder eine weiße Kugel aus der gewählten Urne zu ziehen, hängt von der Verteilung der Kugeln in dieser Urne ab (vgl. Abbildung Angabe).
Die Wahrscheinlichkeiten \(P(\omega)\) der Ergebnisse lassen sich mithilfe der 1. Pfadregel bestimmen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(\{A,S\}) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\]
\[P(\{A,\overline{S}\}) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\]
\[P(\{B,S\}) = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}\]
\[P(\{B,\overline{S}\}) = \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{9}\]
\[P(\{C,\overline{S}\}) = \frac{1}{3} \cdot 1 = \frac{1}{3}\]
Unter Anwendung der 2. Pfadregel ergibt sich folgende Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\):
Unter Anwendung der 2. Pfadregel ergibt sich folgende Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\):
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(G = -1) &= P(\overline{S}) \\[0.8em] &= P(\{A,\overline{S}\}) + P(\{B,\overline{S}\}) + P(\{C,\overline{S}\}) \\[0.8em] &= \frac{1}{6} + \frac{2}{9} + \frac{1}{3} \\[0.8em] &= \frac{3}{18} + \frac{4}{18} + \frac{6}{18} \\[0.8em] &= \frac{13}{18} \end{align*}\]
\[\begin{align*}P(G = a - 1) &= P(S) \\[0.8em] &= P(\{A,S\}) + P(\{B,S\}) \\[0.8em] &= \frac{1}{6} + \frac{1}{9} \\[0.8em] &= \frac{3}{18} + \frac{2}{18} \\[0.8em] &= \frac{5}{18} \end{align*}\]
| \(G = g_{i}\) | \(-1\) | \(a - 1\) |
| \(P(G = g_{i})\) | \(\dfrac{13}{18}\) | \(\dfrac{5}{18}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\)
Erwartungswert \(E(G)\) des Gewinns pro Spiel ermitteln:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*}E(G) &= g_{1} \cdot P(G = g_{1}) + g_{2} \cdot P(G = g_{2}) \\[0.8em] &= (-1) \cdot \frac{13}{18} + (a - 1) \cdot \frac{5}{18} \\[0.8em] &= -\frac{13}{18} + \frac{5}{18}a - \frac{5}{18} \\[0.8em] &= \frac{5}{18}a - 1 \end{align*}\]
Der im Mittel zu erwartende Gewinn pro Spiel muss gleich 0 € sein.
\[\begin{align*} E(G) &= 0 \\[0.8em] \frac{5}{18}a - 1 &= 0 & &| + 1 \\[0.8em] \frac{5}{18}a &= 1 & &| : \frac{5}{18} \\[0.8em] a &= \frac{18}{5} \\[0.8em] &= 3{,}6 \end{align*}\]
Damit bei dem Spiel auf lange Sicht Einsätze und Auszahlungen ausgeglichen sind, muss der Geldbetrag, der ausgezahlt wird, wenn aus einer Urne eine schwarze Kugel gezogen wird, 3,6 € betragen.


