Einer der Graphen I und II in Abbildung 1 ist der Graph einer Stammfunktion von \(f\). Geben Sie diesen Graphen an und begründen Sie Ihre Angabe.
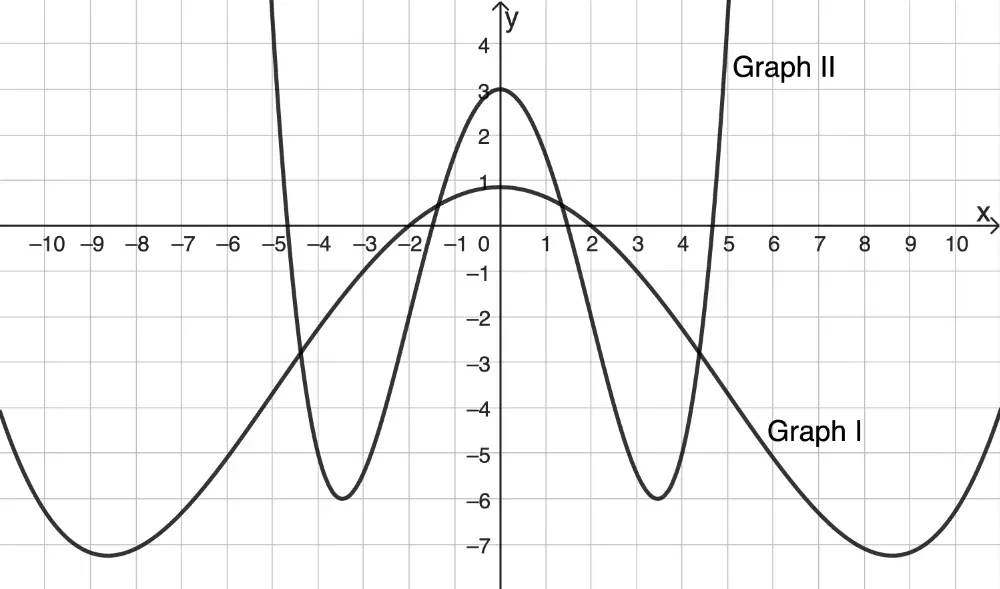Abb. 1
(3 BE)
Lösung zu Teilaufgabe 3b
Graph II ist der Graph einer Stammfunktion von \(f\).
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
Begründung
Da \(2\) mit \(f'(2) = 0\) und \(f''(2) \neq 0\) eine Extremstelle von \(f\) ist (vgl. Teilaufgabe 3a), ist \(2\) mit \(F''(2) = f'(2) = 0\) und \(F'''(2) = f''(2) \neq 0\) eine Wendestelle einer Stammfunktion \(F\) von \(f\).
Wendestellen(n)
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist genau dann eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f''\) an der Stelle \(x_0\) das Vorzeichen wechselt.
Wendestelle(n) und dritte Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) dreimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f'''(x_0) \neq 0\) ist.
Graph II zeigt eine Wendestelle \(\textcolor{#cc071e}{x= 2}\), Graph I hingegen eine Nullstelle \(x = 2\).
