Eine traditionsreiche Kleinkunstbühne bietet verschiedene Veranstaltungen an.
An einem Kabarettabend sind 200 Gäste anwesend.
In der Pause bestellen erfahrungsgemäß 65 % der Gäste einen Brotzeitteller. Es soll angenommen werden, dass die Anzahl der bestellten Brotzeitteller durch eine binomialverteilte Zufallsgröße \(X\) beschrieben werden kann. Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
\(A\): „Es werden genau 130 Brotzeitteller bestellt."
\(B\): „Es werden mehr als 140 Brotzeitteller bestellt."
(3 BE)
Lösung zu Teilaufgabe 1a
\[P(A) = P_{0{,}65}^{200}(X =130) = 0{,}05906 \approx 5{,}9\,%\]
\[\begin{align*}P(B) &= P_{0{,}65}^{200}(X > 140) \\[0.8em] &= 1 - P_{0{,}65}^{200}(X \leq 140) \\[0.8em] &= 0{,}05837 \approx 5{,}8\,\%\end{align*}\]
Ausführliche Erklärung (nicht verlangt)
Betrachtetes Ereignis: „Ein Gast bestellt in der Pause einen Brotzeitteller."
Das betrachtete Ereignis tritt mit der Wahrscheinlichkeit \(\textcolor{#cc071e}{p = 0{,}65}\) ein.
Zufallsgröße \(X\): Anzahl der unter 200 Gästen in der Pause bestellten Brotzeitteller.
Annahme lt. Angabe: Die Zufallsgröße \(X\) ist binomialverteilt nach \(B(\textcolor{#0087c1}{200};\textcolor{#cc071e}{0{,}65})\).
Binomialverteilte Zufallsgröße
Eine Zufallsgröße \(X\), die bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0;1;\dots;n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, heißt binomialverteilt nach \(B(n;p)\).
Binomialverteilung
Die Wahrscheinlichkeitsverteilung einer \(B(n;p)\)-verteilten Zufallsgröße \(X\) heißt Binomialverteilung.
Es gilt: \(\displaystyle P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\) mit \(k = \{0;1;\dots;n\}\) (Bernoulli-Formel)*
Kumulative Verteilungsfunktion einer \(\boldsymbol{B(n;p)}\)-verteilten Zufallsgröße \(\boldsymbol{X}\)
\(F_p^n(k) = P_p^n(X \leq k) = \sum \limits_{i\,=\,0}^k B(n;p;i)\) (von \(X = 0\) bis \(X = k\) aufsummierte Einzelwahrscheinlichkeiten \(B(n;p;i)\))*
* Kann mit dem wissenschaftlichen Taschenrechner (WTR) oder ggf. mit dem Tafelwerk (TW) bestimmt werden.
Wahrscheinlichkeit des Ereignisses \(A\)
\(A\): „Es werden genau 130 Brotzeitteller bestellt."
\[P(A) = P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X = 130}) = B(\textcolor{#0087c1}{200};\textcolor{#cc071e}{0{,}65};\textcolor{#e9b509}{130}) \overset{\text{TW}}{=} 0{,}05906 \approx 5{,}9\,% \quad \text{(TW, linke Spalte)}\]
Anmerkung
\[P(A) = P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X = 130}) = \binom{\textcolor{#0087c1}{200}}{\textcolor{#e9b509}{130}} \cdot \textcolor{#cc071e}{0{,}65}^{\textcolor{#e9b509}{130}} \cdot (1 - \textcolor{#cc071e}{0{,}65})^{\textcolor{#0087c1}{200}\,-\,\textcolor{#e9b509}{130}}\]
Beim Versuch, die Wahrscheinlichkeit mithilfe der Formel von Bernoulli zu berechnen, geraten manche wissenschaftlichen Taschenrechner wegen der großen Werte des Binomialkoeffizienten \(\displaystyle \binom{200}{130}\) an ihre Grenzen und zeigen einen mathematischen Fehler.
Wahrscheinlichkeit des Ereignisses \(B\)
\(B\): „Es werden mehr als 140 Brotzeitteller bestellt."
\[\begin{align*}P(B) &= P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X > 140}) && \textcolor{#e9b509}{\text{„mehr als 140"}} \\[0.8em] &= P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X \geq 141}) && \textcolor{#e9b509}{\text{„mindestens 141"}}\end{align*}\]
Betrachten des Gegenereignisses (mindestens \(k\) Treffer)
Kumulative Wahrscheinlichkeiten der Form \(P(X \geq k)\) einer binomialverteilten Zufallsgröße \(X\) lassen sich im Stochastischen Tafelwerk (TW) nicht nachschlagen. Die Betrachtung des Gegenereignisses \(X \leq k - 1\) ermöglicht das Verwenden des Tafelwerks (rechte Spalte):
\[\underbrace{P(X \geq k)}_{\text{mind.}\,k\,\text{Treffer}} = \underbrace{1 - \underbrace{P(X \leq k - 1)}_{\text{höchstens}\,k\,-\,1\,\text{Treffer}}}_{\text{nicht höchsten}\,k\,-\,1\,\text{Treffer}}\]
Die Wahrscheinlichkeit \(P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X \geq 141})\) dafür, dass mindestens 141 von 200 Gästen in der Pause einen Brotzeitteller bestellen, lässt sich durch die Betrachtung der Wahrscheinlichkeit des Gegenereignisses „... höchstens 140 ..." auf die kumulative Verteilungsfunktion (von \(0\) bis \(k\) aufsummierte Einzelwahrscheinlichkeiten) zurückführen. Diese ist im Tafelwerk (TW) in der rechten Spalte tabellarisiert.
Wahrscheinlichkeiten für „genau \(k\) Treffer" und „höchstens \(k\) Treffer" lassen sich mit dem wissenschaftlichen Taschenrechner (WTR) berechnen und sind für bestimmte Werte der Parameter \(n\) und \(p\) im Tafelwerk (TW) tabellarisiert. Wahrscheinlichkeiten für „mindestens \(k\) Treffer" und „mindestens \(k\) und höchstens \(m\) Treffer müssen auf die kumulative Verteilungsfunktion (aufsummierte Einzelwahrscheinlichkeiten) zurückgeführt werden.

genau \(\boldsymbol{k}\) Treffer
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n \,-\, k}\]
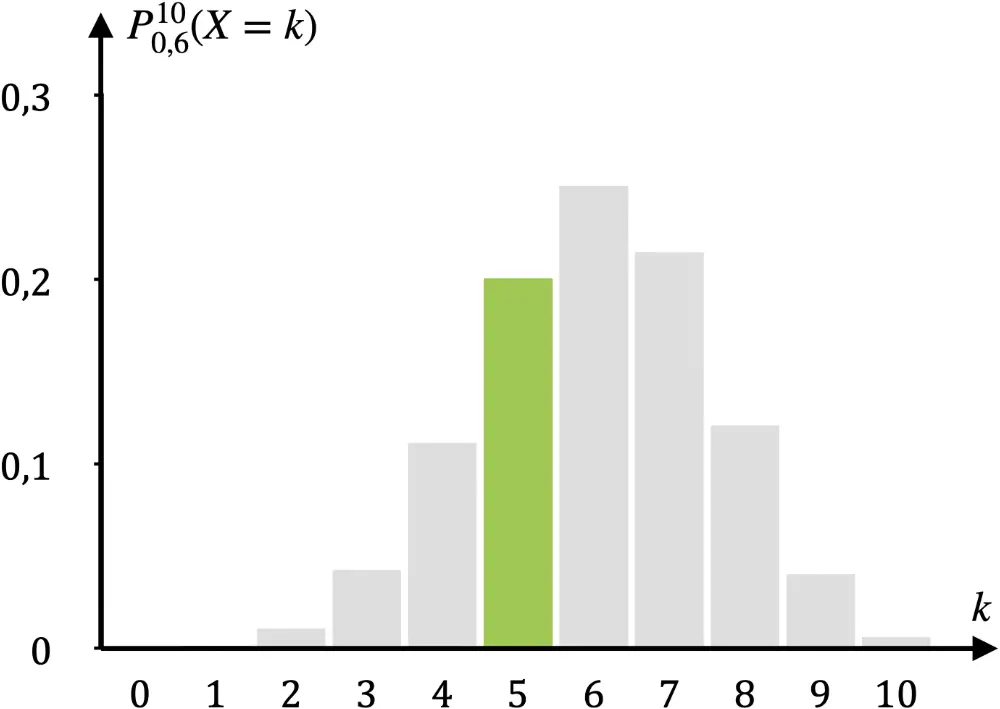
Beispiel: \(n = 10\); \(p = 0{,}6\); \(k = 5\)
\[\textcolor{#89ba17}{P_{0{,}6}^{10}(X = 5)} = B(10;0{,}6;5) = \textcolor{#89ba17}{0{,}20066}\;\text{(WTR/TW)}\]
oder
\begin{align*}\textcolor{#89ba17}{P_{0{,}6}^{10}(X = 5)} &= \binom{10}{5} \cdot 0{,}6^{5} \cdot (1 - 0{,}6)^{10\, -\, 5} \\ &= \textcolor{#89ba17}{0{,}20066} \end{align*}
höchstens \(\boldsymbol{k}\) Treffer
\[\begin{align*}\textcolor{#cc071e}{F_p^n(k)} = \textcolor{#cc071e}{P_{p}^{n}(X \leq k)} =\quad \, &\textcolor{#cc071e}{\sum \limits_{i \,=\, 0}^{k} B(n;p;i)} \\[0.8em] = \quad \,&\textcolor{#89ba17}{P_{p}^{n}(X = 0)} \\[0.8em] +\, &\textcolor{#89ba17}{P_{p}^{n}(X = 1)}\\[0.8em] \;\;\;&\vdots \\[0.8em]+\, &\textcolor{#89ba17}{P_{p}^{n}(X = k)}\end{align*}\]
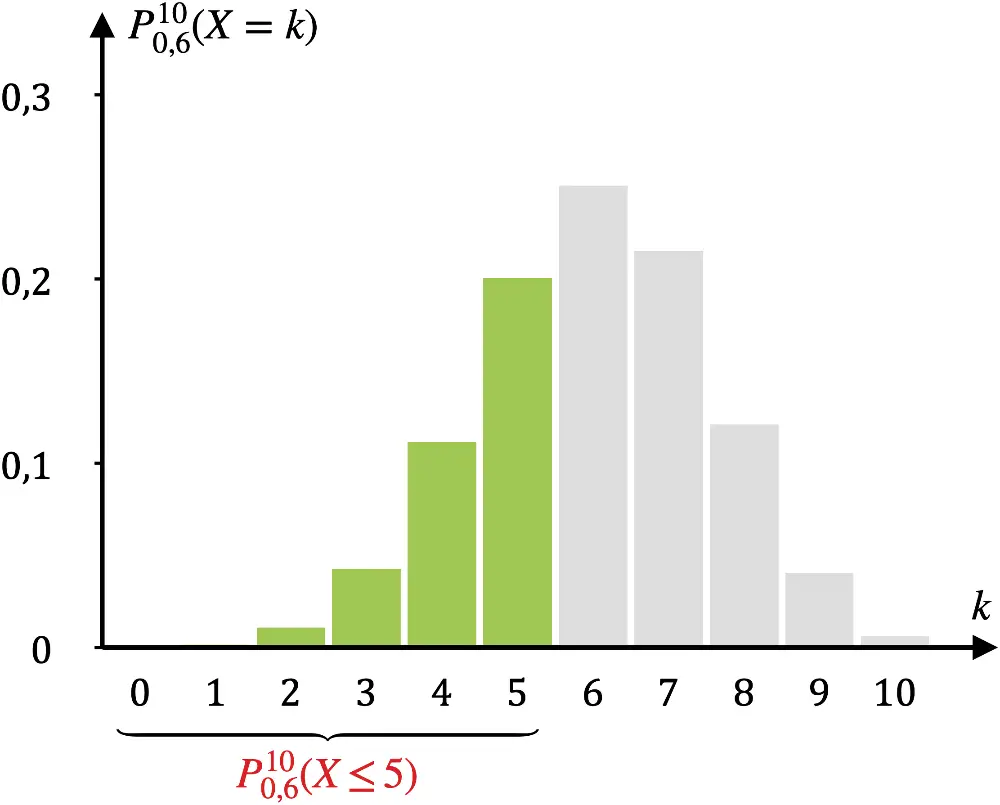
Beispiel: \(n = 10\); \(p = 0{,}6\); \(k = 5\)
\[\begin{align*}\textcolor{#cc071e}{F_{0{,}6}^{10}(5)} = \textcolor{#cc071e}{P_{0{,}6}^{10}(X \leq 5)} &\;\,\,= \textcolor{#cc071e}{\sum \limits_{i \,=\, 0}^{5} B(10;0{,}6;i)} \\[0.8em] &\;\,\,= \textcolor{#cc071e}{0{,}36690}\;\text{(WTR/TW)} \end{align*}\]
weniger als \(\boldsymbol{k}\) Treffer
Entspricht der Berechnung einer Wahrscheinlichkeit für „höchstens \(k - 1\) Treffer": \(P(X < k) = P(X \leq k -1)\)
mindestens \(\boldsymbol{k}\) Treffer
\[\underbrace{\textcolor{#89ba17}{P_{p}^{n}(X \geq k)}}_{\textcolor{#89ba17}{\large{\text{mindestens}\,k}}} = \underbrace{1 - \underbrace{\textcolor{#cc071e}{P_{p}^{n}(X \leq k - 1)}}_{\textcolor{#cc071e}{\large{\text{höchstens}\,k \,-\,1}}}}_{\large{\text{nicht höchstens}\,k\,-\,1}}\]
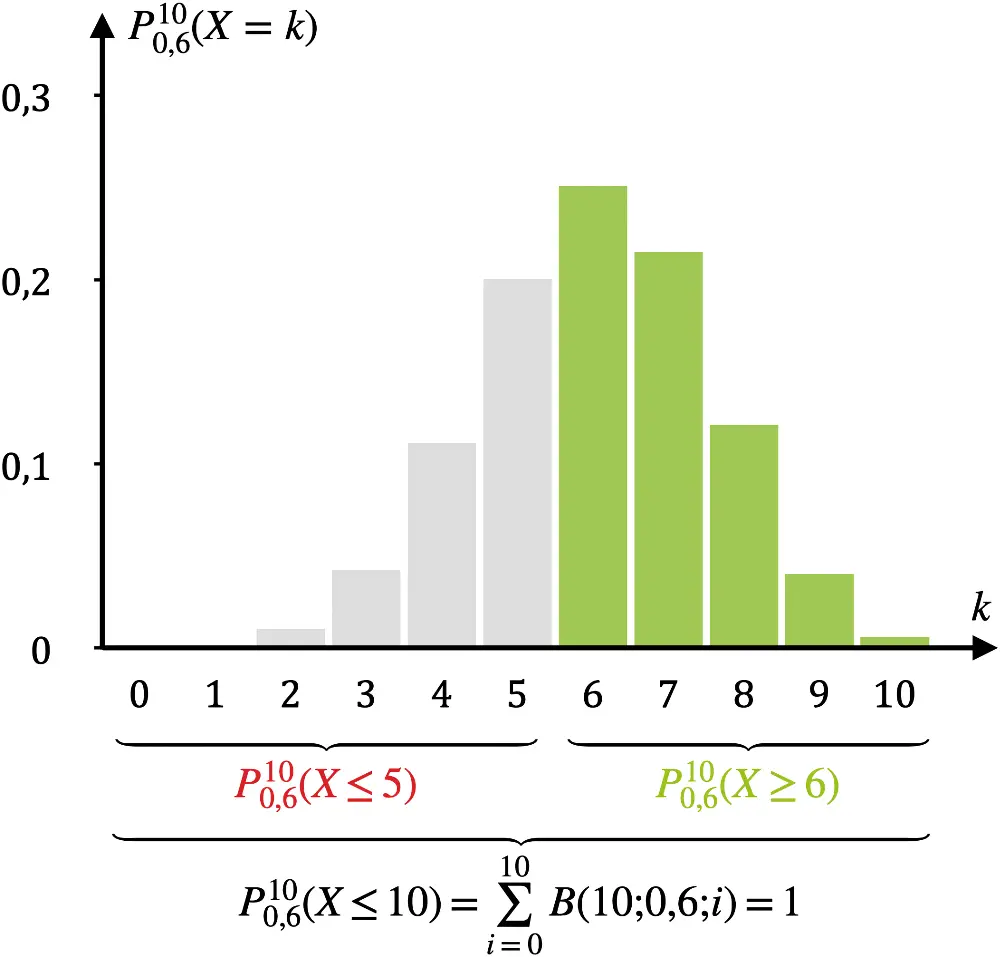
Beispiel: \(n = 10\); \(p = 0{,}6\); \(k = 6\)
\[\begin{align*}\textcolor{#89ba17}{P_{0{,}6}^{10}(X \geq 6)} &= 1 - \textcolor{#cc071e}{P_{0{,}6}^{10}(X \leq 5)} \\[0.8em]&= 1 - \textcolor{#cc071e}{\sum \limits_{i \,=\, 0}^{5}B(10;0{,}6;i)} \\[0.8em]&= 1 - \textcolor{#cc071e}{0{,}36690}\;\text{(WTR/TW)} \\[0.8em] &= \textcolor{#89ba17}{0{,}63310} \end{align*}\]
Veranschaulichung am „Zahlenstrahl":
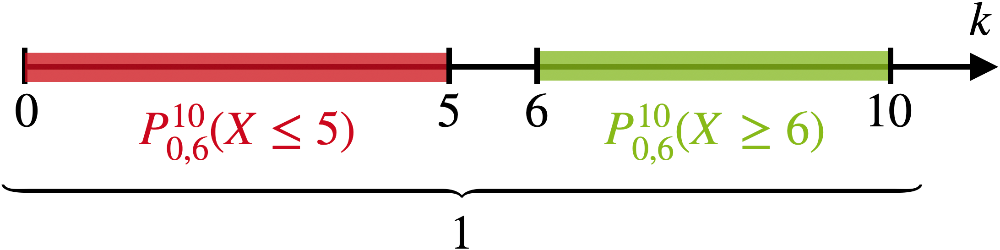
Mehr als \(\boldsymbol{k}\) Treffer
Entspricht der Berechnung einer Wahrscheinlichkeit für „mindestens \(k + 1\) Treffer": \(P(X > k) = P(X \geq k + 1)\).
mindestens \(\boldsymbol{k}\) und höchstens \(\boldsymbol{m}\) Treffer
\[\underbrace{\textcolor{#89ba17}{P_{p}^{n}(k \leq X \leq m)}}_{\textcolor{#89ba17}{\large{\text{mind.}\,k\,\text{u. höchstens}\,m}}} = \underbrace{\textcolor{#0087c1}{P_{p}^{n}(X \leq m)}}_{\textcolor{#0087c1}{\large{\text{höchstens}\,m}}} - \underbrace{\textcolor{#cc071e}{P_{p}^{n}(X \leq k - 1)}}_{\textcolor{#cc071e}{\large{\text{höchstens}\,k\,-\,1}}}\]
Beispiel: \(n = 10\); \(p = 0{,}6\); \(k = 5\); \(m = 8\)
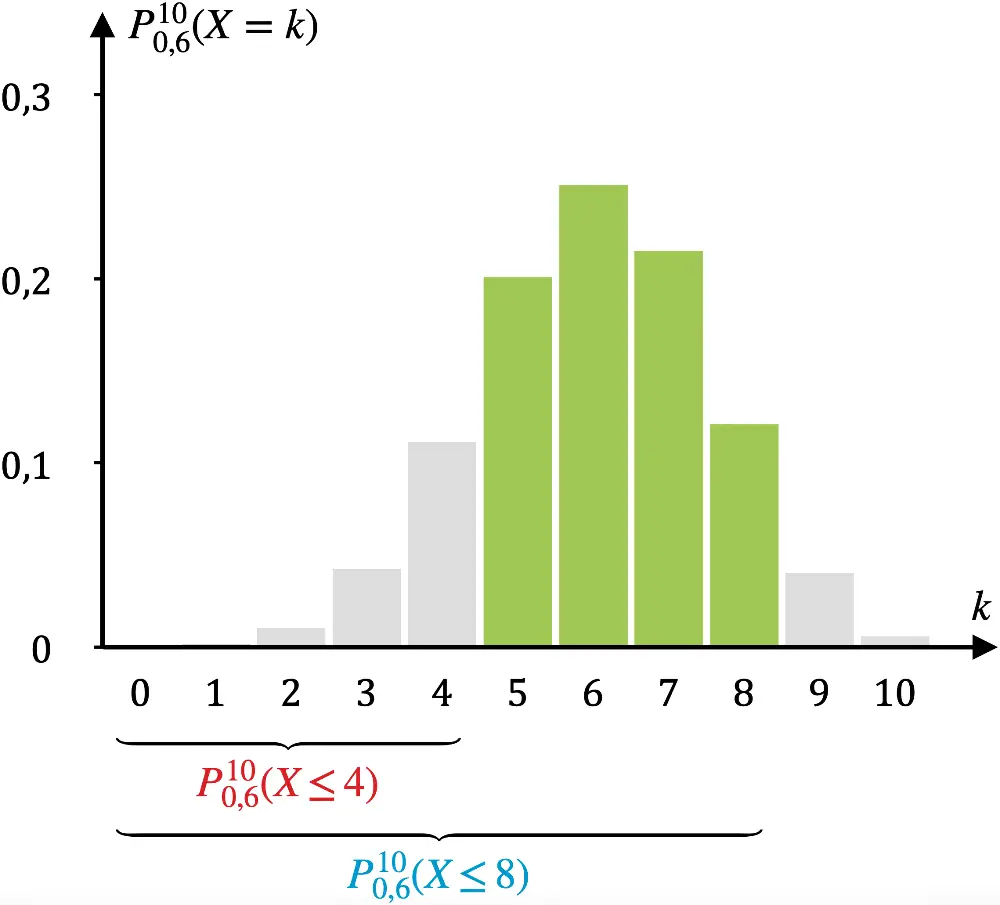
\[\begin{align*} \textcolor{#89ba17}{P_{0{,}6}^{10}(5 \leq X \leq 8)} &= \textcolor{#0087c1}{P_{0{,}6}^{10}(X \leq 8)} - \textcolor{#cc071e}{P_{0{,}6}^{10}(X \leq 4)} \\[0.8em]&= \textcolor{#0087c1}{\sum \limits_{i\, =\, 0}^{8}B(10;0{,}6;i)} - \textcolor{#cc071e}{\sum \limits_{i \,=\, 0}^{4}B(10;0{,}6;i)} \\[0.8em]&= \textcolor{#0087c1}{0{,}95364} - \textcolor{#cc071e}{0{,}16624}\;\text{(WTR/TW)} \\[0.8em]&=\textcolor{#89ba17}{0{,}78740} \end{align*}\]
Veranschaulichung am „Zahlenstrahl":
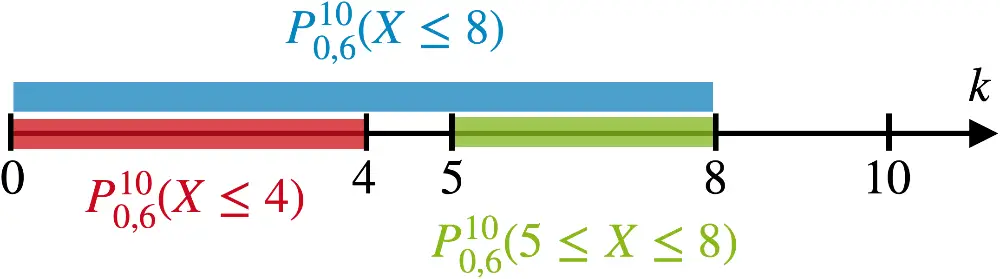
\[\begin{align*}P(B) &= P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X \geq 141}) && \textcolor{#e9b509}{\text{„mindestens 141"}} \\[0.8em] &= 1 - P_{\textcolor{#cc071e}{0{,}65}}^{\textcolor{#0087c1}{200}}(\textcolor{#e9b509}{X \leq 140}) && \text{nicht} \; \textcolor{#e9b509}{\text{„höchstens 140"}} \\[0.8em] &= 1 - \sum \limits_{i \,= \, \textcolor{#e9b509}{0}}^{k\,=\, \textcolor{#e9b509}{140}} B(\textcolor{#0087c1}{200};\textcolor{#cc071e}{0{,}65};i) && \text{TW, rechte Spalte} \\[0.8em] &\hspace{-4px}\overset{\text{TW}}{=} 1 - 0{,}94163 \\[0.8em] &= 0{,}05837 \approx 5{,}8\,\%\end{align*}\]


