
- Beschreiben Sie mithilfe der Abbildung, wie der Graph von \(g\) aus dem Graphen von \(f\) hervorgeht. Geben Sie einen Funktionsterm von \(g\) an, indem Sie \(g\) durch \(f\) ausdrücken.
- Beschreiben Sie, wie der Graph der in \(\mathbb R\) definierten Funktion \(p\colon x \mapsto 4x^2 +8x +4\) aus dem Graphen der in \(\mathbb R\) definierten Funktion \(q\colon x \mapsto x^2\) hervorgeht.
a) Entstehung des Graphen von \(g\) aus dem Graphen von \(f\)
Wie verändern die Parameter \(a\), \(b\), \(c\) und \(d\) den Graphen einer Funktion \(x \mapsto a \cdot f(b \cdot (x + c)) + d\) gegenüber dem Graphen einer Funktion \(x \mapsto f(x)\)?
Erst strecken oder spiegeln, dann verschieben!
Ein Vertauschen der Reihenfolge von Strecken und Verschieben bzw. Spiegel und Verschieben ergibt unterschiedliche Graphen und Funktionsterme.


Strecken in \(\boldsymbol{y}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{a}}\)
\(g(x) = \textcolor{#e9b509}{a} \cdot f(x)\) mit \(a \in \mathbb R\)
\(a < 0\) bewirkt zusätzlich eine Spiegelung an der \(x\)-Achse.

Strecken in \(\boldsymbol{x}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{\dfrac{1}{b}}}\)
\(h(x) = f(\textcolor{#e9b509}{b} \cdot x)\) mit \(b \in \mathbb R\)
\(b < 0\) bewirkt zusätzlich eine Spiegelung an der \(y\)-Achse.

Verschieben in \(\boldsymbol{y}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{d}}\)
\(k(x) = f(x) + \textcolor{#e9b509}{d}\) mit \(d \in \mathbb R\)

Verschieben in \(\boldsymbol{x}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{-c}}\)
\(l(x) = f(x + \textcolor{#e9b509}{c})\) mit \(c \in \mathbb R\)
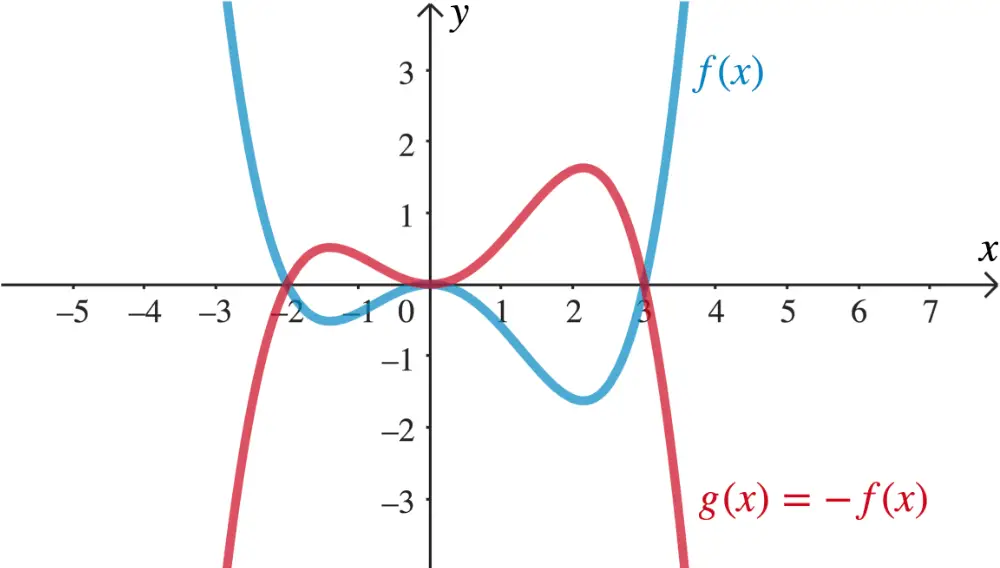
Spiegelung an der \(\boldsymbol{x}\)-Achse
\[g(x) = -f(x)\]

Spiegelung an der \(\boldsymbol{y}\)-Achse
\[h(x) = f(-x)\]
(Darstellungen nicht verlangt)

1. Streckung in \(x\)-Richtung mit dem Faktor \(\frac{1}{2}\)
\[\Rightarrow \; x \mapsto \textcolor{#0087c1}{f(2x)}\]
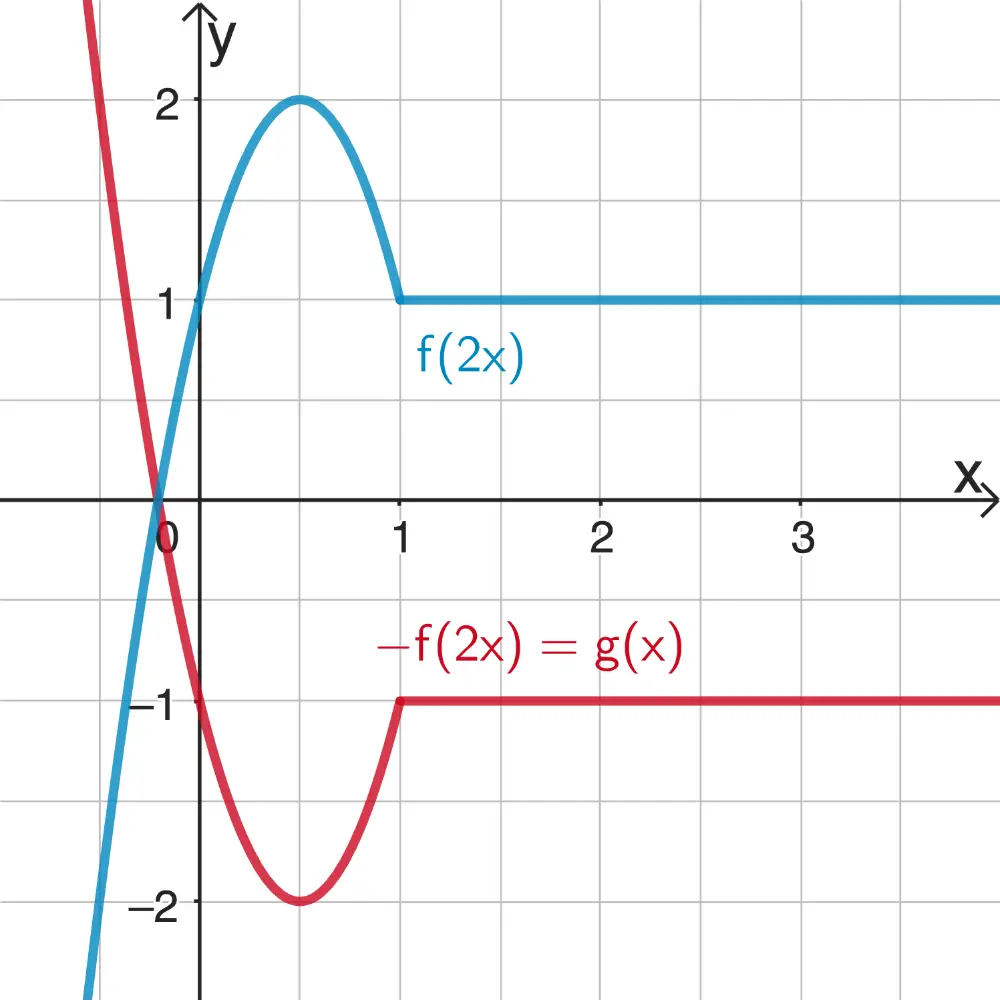
2. Spiegelung an der \(x\)-Achse
\[\Rightarrow \; g(x) = \textcolor{#cc071e}{-f(2x)}\]
oder
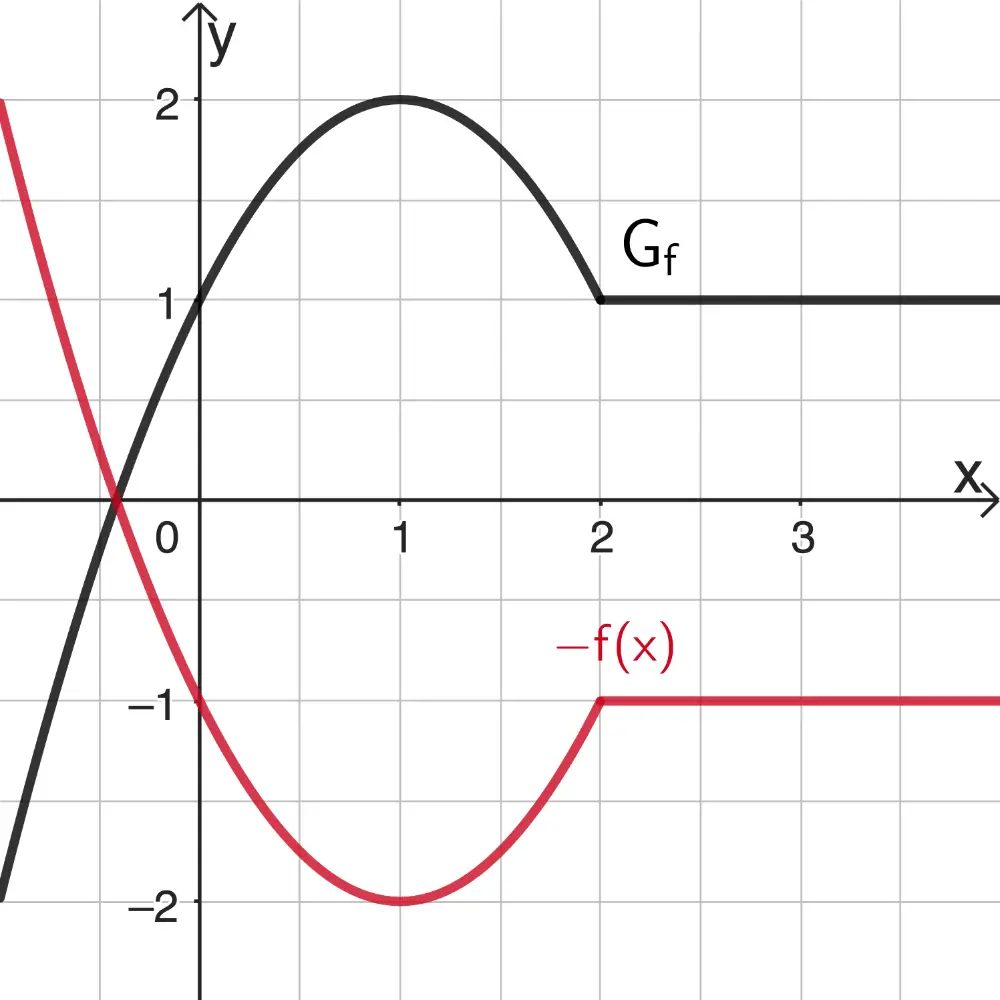
1. Spiegelung an der \(x\)-Achse
\[\Rightarrow \; x \mapsto \textcolor{#cc071e}{-f(x)}\]
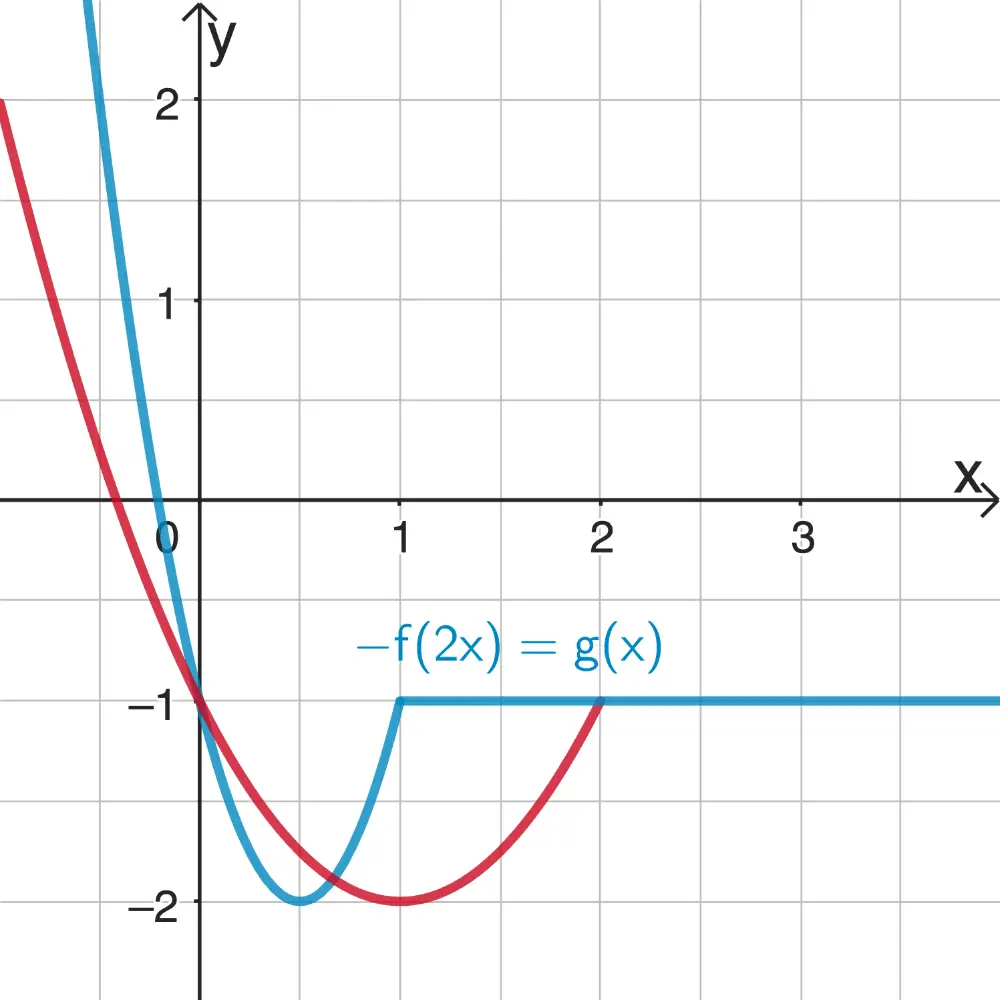
2. Streckung in \(x\)-Richtung mit dem Faktor \(\frac{1}{2}\)
\[\Rightarrow \; g(x) = \textcolor{#0087c1}{-f(2x)}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.7 Entwicklung von Funktionen)
b) Entstehung des Graphen von \(p\) aus dem Graphen von \(g\)
\(q(x) = x^2\)
\(p(x) = 4x^2 +8x +4\)
Der Graph der Funktion \(q\) ist die Normalparabel mit dem Scheitelpunkt \(S(0|0)\).
Um beurteilen zu können, wie die Parabel der quadratischen Funktion \(p\) aus der Normalparabel von \(q\) hervorgeht, wird der Funktionsterm von \(p\) in die Scheitelpunktform gebracht. In diesem Fall kann dafür die erste binomische Formel angewendet werden.
Allgemeine Form
\(f(x) = ax^2 + bx + c\)
Schnittpunkt der Parabel mit der \(y\)-Achse ist \((0|c)\).
Scheitelpunktform
\(f(x) = a(x+d)^2+e\)
Scheitelpunkt der Parabel ist \((-d|e)\).
Nullstellenform
\(f(x) =a(x-x_1)(x-x_2)\)
\(x_1\) und \(x_2\) sind Nullstellen von \(f\).
Besitzt eine quadratische Funktion keine Nullstelle(n), existiert keine Nullstellenform. Besitzt sie nur eine Nullstelle, sind die Scheitelpunktform und die Nullstellenform identisch, z. B. \(f(x) = (x-2)^2\).

\[\begin{align*}p(x) &= 4x^2 +8x +4 &&| \; \text{Faktor}\; 4 \; \text{ausklammern} \\[0.8em] &= 4 \cdot \left( x^2+2x+1\right) &&| \; \text{erste binomische Formel anwenden} \\[0.8em] &= \textcolor{#cc071e}{4} \cdot (x+\textcolor{#0087c1}{1})^2\end{align*}\]
Die Parabel von \(p\) besitzt den Scheitelpunkt \((\textcolor{#0087c1}{-1}|0)\) und den Öffnungsfaktor \(\textcolor{#cc071e}{4}\).
Folglich geht der Graph von \(p\) aus dem Graphen von \(q\) durch
- Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit dem Faktor \(\textcolor{#cc071e}{4}\) und
- Verschiebung in \(\textcolor{#0087c1}{x}\)-Richtung um \(\textcolor{#0087c1}{-1}\)
hervor.
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.1 Ganzrationale Funktion - Quadratische Funktion)


