Gegeben ist die Funktion \(g\) mit \(g(x) = 0{,}7 \cdot e^{0{,}5x} - 0{,}7\) und \(x \in \mathbb R\). Die Funktion \(g\) ist umkehrbar. Die Abbildung 2 zeigt den Graphen \(G_{g}\) von \(g\) sowie einen Teil des Graphen \(G_{h}\) der Umkehrfunktion \(h\) von \(g\).
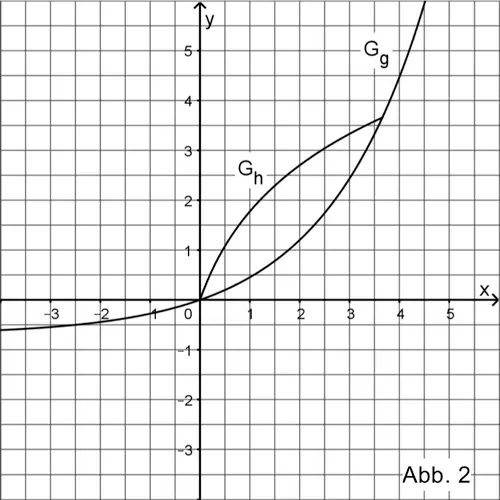
Zeichnen Sie in die Abbildung 2 den darin fehlenden Teil von \(G_{h}\) ein.
(2 BE)
Lösung zu Teilaufgabe 4a
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
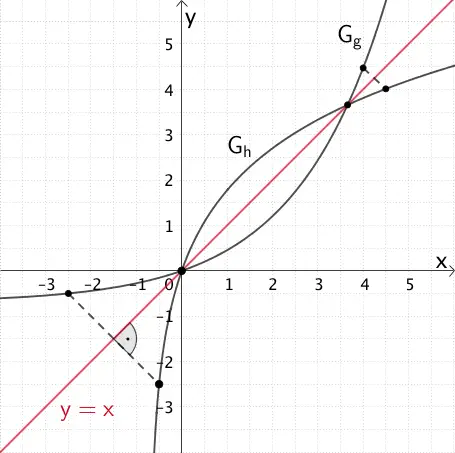
Der Graphen \(G_{h}\) der Umkehrfunktion \(h\) von \(g\) und der Graph \(G_{g}\) sind bezgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\) symmetrisch.
Für die Zeichnung des fehlenden Teils von \(G_{h}\) eignet sich beispielsweise eine Spiegelung der Punkte \((-2{,}5|g(-2{,}5))\) und \((4|g(4))\) an der Winkelhalbierenden. Die Schnittpunkte von \(G_{g}\) und \(G_{h}\) sind Fixpunkte der Spiegelung und liegen auf der Winkelhalbierenden.


