- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(g \colon x \mapsto \sqrt{x + 1} - 2\) mit maximaler Definitionsmenge \(D\).
Geben Sie \(D\) an.
(1 BE)
- Details
- Kategorie: Analysis 2
Bestimmen Sie die Gleichung der Tangente an den Graphen von \(g\) im Punkt \((8|g(8))\).
(4 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(f \colon x \mapsto 1 - \dfrac{1}{x^{2}}\), die die Nullstellen \(x_{1} = -1\) und \(x_{2} = 1\) hat. Abbildung 1 zeigt den Graphen von f, der symmetrisch bezüglich der \(y\)-Achse ist. Weiterhin ist die Gerade \(g\) mit der Gleichung \(y = -3\) gegeben.
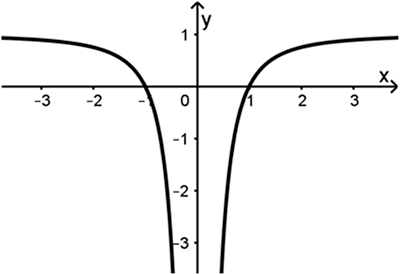Abb. 1
Zeigen Sie, dass einer der Punkte, in denen \(g\) den Graphen von \(f\) schneidet, die \(x\)-Koordinate \(\frac{1}{2}\) hat.
(1 BE)
- Details
- Kategorie: Analysis 2
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von f, die \(x\)-Achse und die Gerade \(g\) einschließen.
(4 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die Schar der in \(\mathbb R\) definierten Funktionen \(p_{k} \colon x \mapsto kx^{2} - 4x - 3\) mit \(k \in \mathbb R \backslash \{0\}\), deren Graphen Parabeln sind.
Bestimmen Sie den Wert von \(k\) so, dass der Punkt \((2|-3)\) auf der zugehörigen Parabel liegt.
(2 BE)
- Details
- Kategorie: Analysis 2
Ermitteln Sie diejenigen Werte von \(k\), für die die jeweils zugehörige Funktion \(p_{k}\) keine Nullstelle besitzt.
(3 BE)
- Details
- Kategorie: Analysis 2
Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion \(f\).
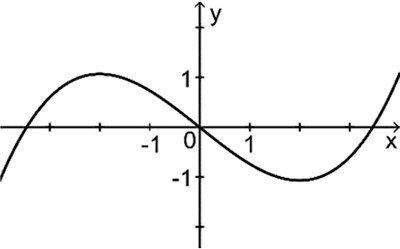Abb. 2
Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von \(f\). Geben Sie diesen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.
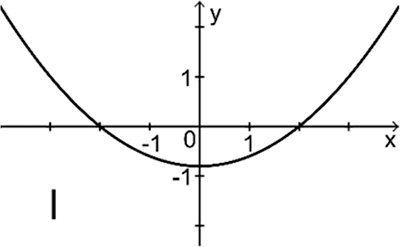
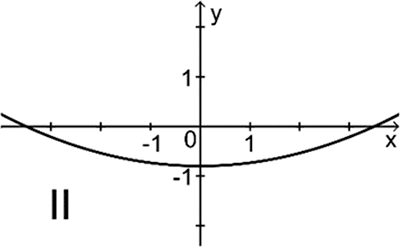
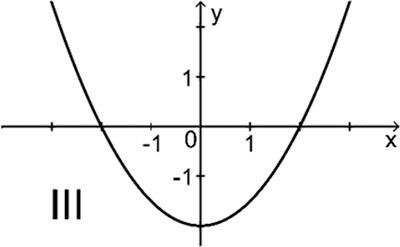Abb. 3
(3 BE)
- Details
- Kategorie: Analysis 2
Die Funktion \(F\) ist eine Stammfunktion von \(f\). Geben Sie das Monotonieverhalten von \(F\) im Intervall \([1;3]\) an. Begründen Sie Ihre Angabe.
(2 BE)
