Der Punkt \(L\), der vertikal über dem Mittelpunkt der Kante \([A_{1}A_{2}]\) liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die 12 m über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet - mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände - das gesamte Gelände um die Halle.
Die Punkte \(L\), \(B_{2}\) und \(B_{3}\) legen eine Ebene \(F\) fest. Ermitteln Sie eine Gleichung von \(F\) in Normalenform.
(zur Kontrolle: \(F \colon 3x_{1} + x_{2} + 5x_{3} - 90 = 0\))
(5 BE)
Lösung zu Teilaufgabe d
Koordinaten des Punktes \(L\)
Der Mittelpunkt \(M_{[A_{1}A_{2}]}\) der Strecke \([A_{1}A_{2}]\) hat mit \(A_{1}(0|0|0)\) und \(A_{2}(\textcolor{#e9b509}{20}|0|0)\) hat die Koordinaten \(M_{[A_{1}A_{2}]}(\textcolor{#e9b509}{10}|0|0)\). Da die Lichtquelle 12 m vertikal (senkrecht) über \(M_{[A_{1}A_{2}]}\) liegt, folgt: \(L(\textcolor{#e9b509}{10}|0|\textcolor{#89ba17}{12})\).
Oder ausführlich dokumentiert:
\(A_{1}(0|0|0)\), \(A_{2}(20|0|0)\)
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*}\overrightarrow{M}_{[A_{1}A_{2}]} &= \frac{1}{2} \cdot (\overrightarrow{A_{1}} + \overrightarrow{A_{2}}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 20 \\ 0 \\ 0 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 20 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 10 \\ 0 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad M_{[A_{1}A_{2}]}(10|0|0)\]
Da die Lichtquelle 12 m vertikal (senkrecht) über \(M_{[A_{1}A_{2}]}\) liegt, folgt: \(L(10|0|\textcolor{#89ba17}{12})\).
Gleichung der Ebene \(F\) in Normalenform
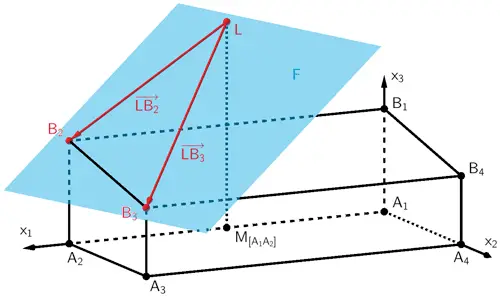
Beispielsweise liefert das Vektorprodukt \(\overrightarrow{LB_{2}} \times \overrightarrow{LB_{3}}\) der beiden linear unabhängigen Verbindungsvektoren \(\textcolor{#cc071e}{\overrightarrow{LB_{2}}}\) und \(\textcolor{#cc071e}{\overrightarrow{LB_{3}}}\) einen Normalenvektor \(\overrightarrow{n}\) der Ebene \(F\). Als Aufpunkt wählt man einen der Punkte \(L\), \(B_{2}\) oder \(B_{3}\). Damit lässt sich eine Gleichung der Ebene \(F\) in Normalenform angeben.
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} = k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} \neq k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Der Ansatz kann mithilfe der Normalenform in Vektordarstellung oder in Koordinatendarstellung erfolgen. Die Aufgabenstellung nennt zur Kontrolle eine Gleichung der Ebene \(F\) in Normalenform in Koordinatendarstellung.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Verbindungsvektoren \(\overrightarrow{LB_{2}}\) und \(\overrightarrow{LB_{3}}\) bestimmen:
\(L(10|0|12)\), \(B_{2}(20|0|6)\), \(B_{3}(20|10|4)\) (vgl. Teilaufgabe a)
\[\overrightarrow{LB_{2}} = \overrightarrow{B_{2}} - \overrightarrow{L} = \begin{pmatrix} 20 \\ 0 \\ 6 \end{pmatrix} - \begin{pmatrix} 10 \\ 0 \\ 12 \end{pmatrix} = \begin{pmatrix} 10 \\ 0 \\ -6 \end{pmatrix}\]
\[\overrightarrow{LB_{3}} = \overrightarrow{B_{3}} - \overrightarrow{L} = \begin{pmatrix} 20 \\ 10 \\ 4 \end{pmatrix} - \begin{pmatrix} 10 \\ 0 \\ 12 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ -8 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}\) der Ebene \(F\) ermitteln:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \overrightarrow{LB_{2}} \times \overrightarrow{LB_{3}} &= \begin{pmatrix} 10 \\ 0 \\ -6 \end{pmatrix} \times \begin{pmatrix} 10 \\ 10 \\ -8 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 & \cdot & (-8) & - & (-6) & \cdot & 10 \\ (-6) & \cdot & 10 & - & 10 & \cdot & (-8) \\ 10 & \cdot & 10 & - & 0 & \cdot & 10 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 60 \\ 20 \\ 100 \end{pmatrix} = 20 \cdot \begin{pmatrix} 3 \\ 1 \\ 5 \end{pmatrix} \end{align*}\]
Der Vektor \(\overrightarrow{n} = \begin{pmatrix} 3 \\ 1 \\ 5 \end{pmatrix}\) ist also ein Normalenvektor der Ebene \(F\).
Gleichung der Ebene \(F\) in Normalenform beschreiben:
Der Punkt \(L(10|0|12)\) dient beispielsweise als Aufpunkt.
1. Möglichkeit: Ansatz mit der Normalenform in Vektordarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[\begin{align*}F \colon &\overrightarrow{n} \circ (\overrightarrow{X} - \overrightarrow{L}) = 0 \\[0.8em] F \colon &\begin{pmatrix} 3 \\ 1 \\ 5 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 10 \\ 0 \\ 12 \end{pmatrix} \right] = 0 \\[0.8em] &\textcolor{#0087c1}{3 \cdot (x_{1} - 10) + 1 \cdot (x_{2} - 0) + 5 \cdot (x_{3} - 12) = 0} \\[0.8em] &\textcolor{#0087c1}{3x_{1} - 30 + x_{2} + 5x_{3} - 60 = 0} \\[0.8em] \textcolor{#0087c1}{F \colon \,} &\textcolor{#0087c1}{3x_{1} + x_{2} + 5x_{3} - 90 = 0} \end{align*}\]
Anmerkung:
Da die Aufgabe keine bestimmte Darstellung der Normalenform verlangt, ist das Ausmultiplizieren des Skalarprodukts, d.h. die Umwandlung in die Koordinatendarstellung, nicht unbedingt notwendig.
2. Möglichkeit: Ansatz mit der Normalenform in Koordinatendarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\(\overrightarrow{n} = \begin{pmatrix} \textcolor{#e9b509}{3} \\ \textcolor{#e9b509}{1} \\ \textcolor{#e9b509}{5} \end{pmatrix}\), \(L(\textcolor{#89ba17}{10}|\textcolor{#89ba17}{0}|\textcolor{#89ba17}{12})\)
\[\begin{align*} &F \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0 \\[0.8em] &F \colon \textcolor{#e9b509}{3} \cdot x_{1} + \textcolor{#e9b509}{1} \cdot x_{2} + \textcolor{#e9b509}{5} \cdot x_{3} + n_{0} = 0 \end{align*}\]
\[\begin{align*} L \in F \colon 3 \cdot \textcolor{#89ba17}{10} + \textcolor{#89ba17}{0} + 5 \cdot \textcolor{#89ba17}{12} + n_{0} &= 0 \\[0.8em] 30 + 60 + n_{0} &= 0 \\[0.8em] 90 + n_{0} &= 0 &&| - 90 \\[0.8em] n_{0} &= -90 \end{align*}\]
\[\Longrightarrow \quad F \colon 3x_{1} + x_{2} + 5x_{3} - 90 = 0\]


