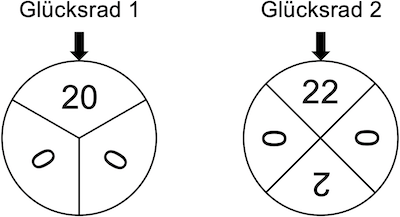
Um Geld für die beiden Aktionen einzunehmen, bietet die SMV auf dem Schulfest das Spiel „2022" an. Bei dem Spiel werden zwei Glücksräder mit drei bzw. vier gleich großen Sektoren verwendet, die wie in Abbildung 1 beschriftet sind. Für einen Einsatz von 3 € darf man jedes der beiden Glücksräder einmal drehen. Für jede Ziffer 2, die auf den erzielten Sektoren steht, werden 2 € ausbezahlt. Die Zufallsgröße \(Z\) beschreibt, wie oft die Ziffer 2 auf den erzielten Sektoren insgesamt vorkommt.
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von \(Z\). Bestimmen Sie die Wahrscheinlichkeiten \(p_1\) und \(p_2\).
| \(k\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(P(Z = k)\) | \(\dfrac{1}{3}\) | \(p_1\) | \(p_2\) | \(\dfrac{1}{12}\) |
(zur Kontrolle: \(p_2 = \frac{1}{4}\))
(3 BE)
Lösung zu Teilaufgabe 2a
\[p_1 = \frac{2}{3} \cdot \frac{1}{4} + \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{3}\]
\[p_2 = \frac{2}{3} \cdot \frac{1}{4} + \frac{1}{3} \cdot \frac{1}{4} = \frac{1}{4}\]
oder
\[p_2 = 1 - \left( \frac{1}{3} + \frac{1}{3} + \frac{1}{12} \right) = \frac{1}{4}\]
Ausführliche Erklärung (nicht verlangt)
„... zwei Glücksräder mit drei bzw. vier gleich großen Sektoren ..." (vgl. Angabe)
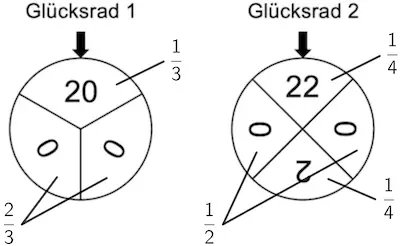
Glücksrad 1: \(P(\{20\}) = \dfrac{1}{3}\); \(P(\{0\}) = \dfrac{2}{3}\)
Glücksrad 2: \(P(\{22\}) = \dfrac{1}{4}\); \(P(\{2\}) = \dfrac{1}{4}\); \(P(\{0\}) = \dfrac{1}{2}\)
Berechnung der Wahrscheinlichkeit \(p_1\)
Jedes der beiden Glücksräder wird einmal gedreht.
\(Z\): Anzahl, wie oft die Ziffer 2 auf den erzielten Sektoren insgesamt vorkommt.
\(p_1 = P(\textcolor{#89ba17}{Z = 1})\)
Die Zufallsgröße \(\boldsymbol{Z}\) nimmt den Wert \(\boldsymbol{1}\) an, wenn mit Glücksrad 1 die Ziffer 0 und mit Glücksrad 2 die Ziffer 2 erzielt wird, oder wenn mit Glücksrad 1 die Ziffer 20 und mit Glücksrad 2 die Ziffer 0 erzielt wird.
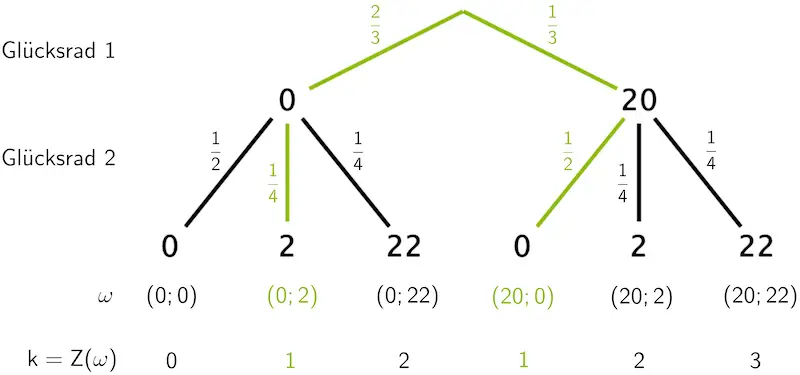
Veranschaulichung der Berechnung von \(p_1 = P(\textcolor{#89ba17}{Z = 1})\) mithilfe eines Baumdiagramms
Mithilfe der 1. und der 2. Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}p_1 = P(\textcolor{#89ba17}{Z = 1}) &= P(\{\textcolor{#89ba17}{(0;2)}\}) + P(\{\textcolor{#89ba17}{(20;0)}\}) \\[0.8em] &= \underbrace{\underbrace{\textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{4}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{1}{3}} \cdot \textcolor{#89ba17}{\frac{1}{2}}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= \frac{2}{12} + \frac{1}{6} = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}\end{align*}\]
Berechnung der Wahrscheinlichkeit \(p_2\)
Jedes der beiden Glücksräder wird einmal gedreht.
\(Z\): Anzahl, wie oft die Ziffer 2 auf den erzielten Sektoren insgesamt vorkommt.
\(p_2 = P(\textcolor{#89ba17}{Z = 2})\)
Die Zufallsgröße \(\boldsymbol{Z}\) nimmt den Wert \(\boldsymbol{2}\) an, wenn mit Glücksrad 1 die Ziffer 0 und mit Glücksrad 2 die Ziffer 22 erzielt wird, oder wenn mit Glücksrad 1 die Ziffer 20 und mit Glücksrad 2 die Ziffer 2 erzielt wird.
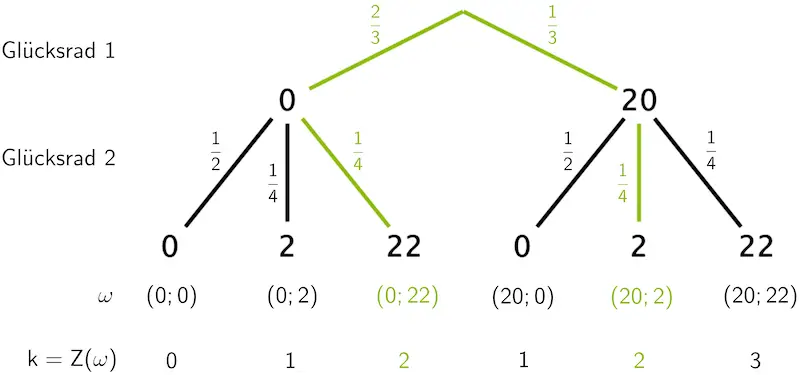
Veranschaulichung der Berechnung von \(p_2 = P(\textcolor{#89ba17}{Z = 2})\) mithilfe eines Baumdiagramms
Mithilfe der 1. und der 2. Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}p_2 = P(\textcolor{#89ba17}{Z = 2}) &= P(\{\textcolor{#89ba17}{(0;22)}\}) + P(\{\textcolor{#89ba17}{(20;2)}\}) \\[0.8em] &= \underbrace{\underbrace{\textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{4}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{1}{3}} \cdot \textcolor{#89ba17}{\frac{1}{4}}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= \frac{2}{12} + \frac{1}{12} = \frac{3}{12} = \frac{1}{4}\end{align*}\]
Alternative
Die Summe aller Wahrscheinlichkeiten der Werte von \(Z\) ist eins.
| \(k\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(P(Z = k)\) | \(\textcolor{#e9b509}{\dfrac{1}{3}}\) | \(\textcolor{#e9b509}{\dfrac{1}{3}}\) | \(p_2\) | \(\textcolor{#e9b509}{\dfrac{1}{12}}\) |
\[\begin{align*}\sum P(Z = k) = 1 \enspace \Rightarrow \enspace p_2 &= 1 - \left( \textcolor{#e9b509}{\frac{1}{3}} + \textcolor{#e9b509}{\frac{1}{3}} + \textcolor{#e9b509}{\frac{1}{12}} \right) \\[0.8em] &= 1 - \left( \frac{4}{12} + \frac{4}{12} + \frac{1}{12} \right) \\[0.8em] &= 1 - \frac{9}{12} = \frac{3}{12} = \frac{1}{4}\end{align*}\]


