Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen Tunnelquerschnitt, der senkrecht zum Tunnelverlauf liegt. Dazu beschreiben sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in einem Koordinatensystem. Der Querschnitt des Tunnelbodens liegt dabei auf der \(x\)-Achse, sein Mittelpunkt \(M\) im Ursprung des Koordinatensystems; eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Für den Tunnelquerschnitt sollen folgende Bedingungen gelten:
I Breite des Tunnelbodens: b = 10 m
II Höhe des Tunnels an der höchsten Stelle: h = 5 m
III Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch.
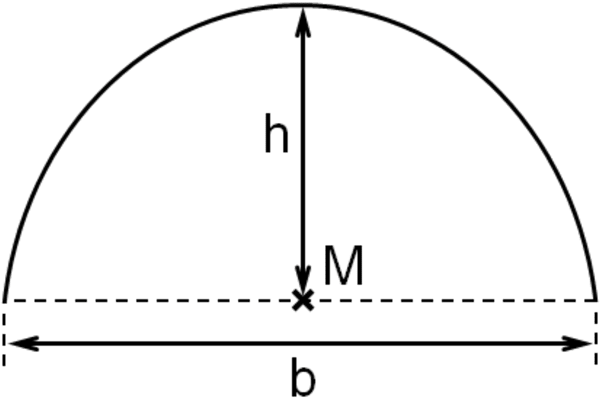
Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion \(p \colon x \mapsto -0{,}2x^{2} + 5\) mit dem Definitionsbereich \(D_{p} = [-5;5]\).
Zeigen Sie, dass die Bedingungen I und II in diesem Modell erfüllt sind. Berechnen Sie die Größe des spitzen Winkels, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden trifft.
(6 BE)
Lösung zu Teilaufgabe 1a
Nullstelle, Scheitelpunkt, Extremstelle des Graphen einer quadratischen Funktion, Steigungswinkel einer Tangente
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
Nachweis, dass Bedingung I erfüllt ist
Bedingung I:
Breite des Tunnelbodens: b = 10 m
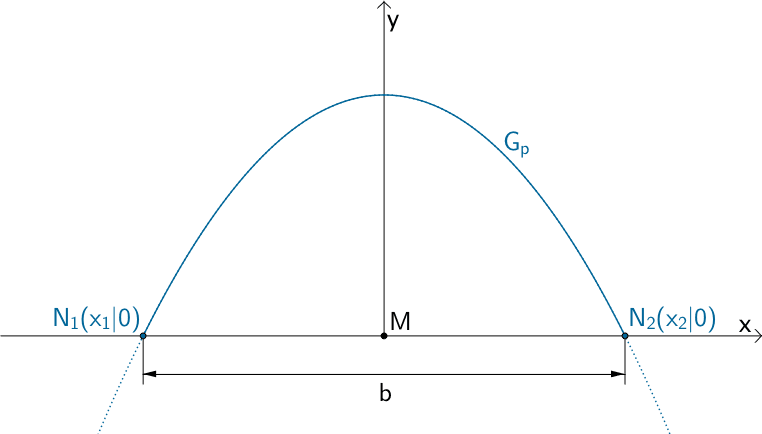
Der Graph der quadratischen Funktion \(p\) ist eine nach unten geöffnet Parabel. Die Länge der Strecke \([N_{1}N_{2}]\) zwischen den Schnittpunkten \(N_{1}(x_{1}|0)\) und \(N_{2}(x_{2}|0)\) der Parabel mit der \(x\)-Achse entspricht bei dieser Modellierung der Breite b des Tunnelbodens.
\[\begin{align*} p(x) &= 0 \\[0.8em] -0{,}2x^{2} + 5 &= 0 & &| - 5 \\[0.8em] -0{,}2x^{2} &= -5 & &| : (-0{,}2) \\[0.8em] x^{2} &= 25 & &| \; \sqrt{\enspace} \\[0.8em] x_{1,2} &= \pm 5 \end{align*}\]
\[x_{1} = -5; \; x_{2} = 5\]
\[\overline{N_{1}N_{2}} = x_{2} - x_{1} = 5 - (-5) = 10\]
Bedingung I ist mit b = 10 m erfüllt.
Nachweis, dass Bedingung II erfüllt ist
Bedingung II:
Höhe des Tunnelbodens an der höchsten Stelle: h = 5 m
1. Lösungsansatz: Scheitelpunkt der Parabel von \(p\)
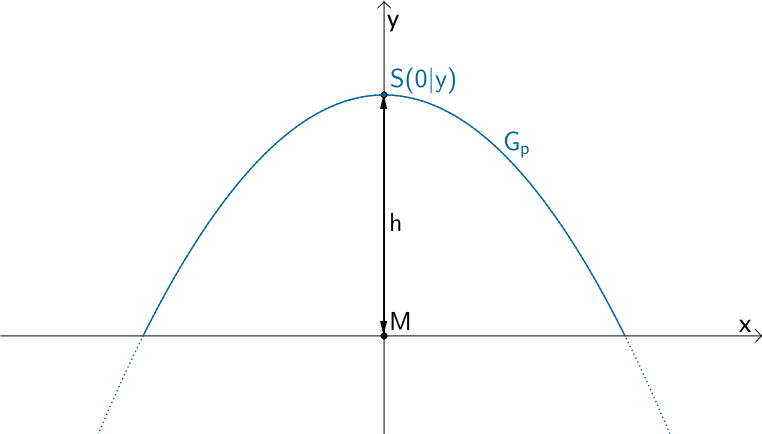
Die \(y\)-Koordiante des Scheitelpunkts \(S\) der nach unten geöffneten Parabel der quadratischen Funktion \(p\) entspricht bei dieser Modellierung der Höhe h des Tunnels an der höchsten Stelle.
Scheitelpunkt der Parabel von \(p\):
Die quadratische Funktion \(p\) lässt sich ohne Rechenaufwand in der Scheitelpunlktform darstellen, aus der die Scheitelpunktkoordinaten direkt entnommen werden können.
Quadratische Funktion:
\[f(x) = ax^2 + bx + c\,; \quad a, b, c \, \in \, \mathbb R\,, a \neq 0\]
Scheitelpunktform
\[f(x) = a(x - d)^2 + e\]
Scheitelpunkt
\[S\,(d|e) \qquad d = -\frac{b}{2a}\,; \quad e = c - \frac{b^2}{4a}\]
\[\begin{align*} p(x) &= -0{,}2x^{2} + 5 \\[0.8em] &= -0{,}2 \cdot (x - 0)^{2} + 5 \end{align*}\]
\[\Longrightarrow \quad S(0|5)\]
Bedingung II ist mit h = 5 m erfüllt.
Alternative Argumentation:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Die Parabel der quadratischen Funktion \(p \colon x \mapsto -0{,}2x^{2} + 5\) ist gegenüber der Parabel der Funktion \(x \mapsto -0{,}2x^{2}\), deren Scheitelpunkt im Koordinatenursprung liegt, um 5 in positive \(y\)-Richtung verschoben.
\[\Longrightarrow \quad S(0|5)\]
Bedingung II ist mit h = 5 m erfüllt.
2. Lösungsansatz: Extrempunkt des Graphen von \(p\) bestimmen
Notwendige Bedingung für eine Extremstelle des Graphen der Funktion \(p\):
\[p'(x) \overset{!}{=} 0\]
Erste Ableitung \(p'\) bilden:
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} p'(x) &= -0{,}2 \cdot 2 \cdot x^{1} \\[0.8em] &= -0{,}4x \end{align*}\]
Nullstelle von \(p'\) ermitteln:
\[\begin{align*} p'(x) &= 0 \\[0.8em] -0{,}4x &= 0 \\[0.8em] x &= 0 \end{align*}\]
Nachweis, der Art des Extrempunkts:
1. Möglichkeit: Extrempunkt einer Parabel
Der Graph der Funktion \(p \colon x \mapsto -0{,}2x^{2} + 5\) ist eine nach unten geöffnete Parabel (Öffnungsfaktor \(a\) < 0). Eine Parabel besitzt genau einen Extrempunkt. Im Falle des Graphen der Funktion \(p\) muss dies ein Hochpunkt \(HoP\) sein.
\[\Longrightarrow \quad HoP(0|p(0))\]
2. Möglichkeit: Monotoniekriterium
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[p'(x) = -0{,}4x\]
\[\left. \begin{align*} &p'(x) > 0 \enspace \text{für} \enspace x < 0 \\[0.8em] &p'(0) = 0 \\[0.8em] &p'(x) < 0 \enspace \text{für} \enspace x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt} \; HoP(0|p(0))\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \(x\) | \(x < 0\) | \(x = 0\) | \(x > 0\) |
| \(p'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{p}\) | \(\nearrow\) | \(HoP(0|p(0))\) | \(\searrow\) |
3. Möglichkeit: Art von Extrempunkten mithilfe der 2. Ableitung
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(p''\) bilden:
\[p'(x) = -0{,}4x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[p''(x) = -0{,}4\]
\[\left. \begin{align*} &p'(0) = 0 \\[0.8em] &p''(0) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt} \; HoP(0|p(0))\]
Schlussfolgerung:
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
\[HoP(0|p(0))\]
\[p(0) = -0{,}2 \cdot 0^{2} + 5 = 5\]
\[\Longrightarrow \quad HoP(0|5)\]
Bedingung II ist mit h = 5 m erfüllt.
Größe des spitzen Winkels, unter dem die linke Tunnelwand auf den Tunnelboden trifft
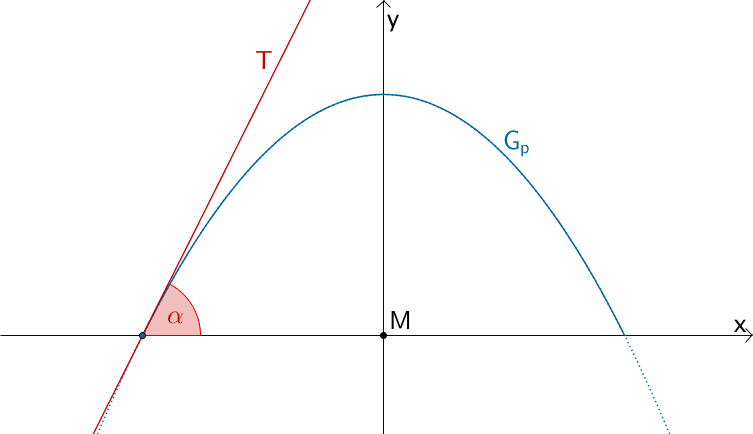
Der spitze Winkel, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden auftrifft, entspricht dem Steigungswinkel \(\alpha\) der Tangente \(T\) an den Graphen der Funktion \(p\) im Punkt \((-5|0)\) (vgl. Nachweis von Bedingung I)
Für die Steigung \(m_{T}\) der Tangente \(T\) an \(G_{p}\) im Punkt \((-5|0)\) gilt:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = p'(-5)\]
Für den Steigungswinkel \(\alpha\) der Tangente \(T\) gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan \alpha = m_{T}\]
\[\Longrightarrow \quad \tan \alpha = p'(-5)\]
Steigungswinkel \(\alpha\) berechnen:
\[p'(x) = -0{,}4x\]
\[\begin{align*} \tan \alpha &= p'(-5) \\[0.8em] &= -0{,}4 \cdot (-5) \\[0.8em] &= 2 & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[2.4em] \alpha &\approx 63{,}43^{\circ} \end{align*}\]
Bei dieser Modellierung trifft die linke Tunnelwand unter einem spitzen Winkel von ca. 63.43° auf den Tunnelboden auf.

